廣大碼農(nóng)同學(xué)們大多都有個(gè)共識(shí)，認(rèn)為算法是個(gè)硬骨頭，很難啃，悲劇的是啃完了還未必有用——除了面試的時(shí)候。實(shí)際工程中一般都是用現(xiàn)成的模塊，一般只需了解算法的目的和時(shí)空復(fù)雜度即可。

不過(guò)話說(shuō)回來(lái)，面試的時(shí)候面算法，包括面項(xiàng)目中幾乎不大可能用到的算法，其實(shí)并不能說(shuō)是毫無(wú)道理的。算法往往是對(duì)學(xué)習(xí)和理解能力的一塊試金石，難的都能掌握，往往容易的事情不在話下。志于高者得于中。反之則不成立。另一方面，雖說(shuō)教科書(shū)算法大多數(shù)都是那些即便用到也是直接拿模塊用的，但不幸的是，我們這群搬磚頭的有時(shí)候還非得做些發(fā)明家的事情：要么是得把算法當(dāng)白盒加以改進(jìn)以滿足手頭的特定需求；要么干脆就是要發(fā)明輪子。所以，雖說(shuō)面試的算法本身未必用得到，但熟悉各種算法的人通常更可能熟悉算法的思想，從而更可能具備這里說(shuō)的兩種能力。

那么，為什么說(shuō)算法很難呢？這個(gè)問(wèn)題只有兩種可能的原因：

算法本身就很難。也就是說(shuō)，算法這個(gè)東西對(duì)于人類的大腦來(lái)說(shuō)本身就是個(gè)困難的事兒。

講得太爛。

下面會(huì)說(shuō)明，算法之所以被絕大多數(shù)人認(rèn)為很難，以上兩個(gè)原因兼具。

我們說(shuō)算法難的時(shí)候，有兩種情況：一種是學(xué)算法難。第二種是設(shè)計(jì)算法難。對(duì)于前者，大多數(shù)人（至少我當(dāng)年如此）學(xué)習(xí)算法幾乎是在背算法，就跟背菜譜似的（“Cookbook”是深受廣大碼農(nóng)喜愛(ài)的一類書(shū)），然而算法和菜譜的區(qū)別在于，算法包含的細(xì)節(jié)復(fù)雜度是菜譜的無(wú)數(shù)倍，算法的問(wèn)題描述千變?nèi)f化，邏輯過(guò)程百轉(zhuǎn)千回，往往看得人愁腸百結(jié)，而相較之下任何菜譜涉及到的基本元素也就那么些（所以程序員肯定都具有成為好廚師的潛力:D）注意，即便你看了算法的證明，某種程度上還是“背”（為什么這么說(shuō)，后面會(huì)詳述）。我自己遇到新算法基本是會(huì)看證明的，但是發(fā)現(xiàn)沒(méi)多久還是會(huì)忘掉，這是死記硬背的標(biāo)準(zhǔn)癥狀。如果你也啃過(guò)算法書(shū)，我相信很大可能性你會(huì)有同感：為什么當(dāng)時(shí)明明懂了，但沒(méi)多久就忘掉了呢？為什么當(dāng)時(shí)明明非常理解其證明，但沒(méi)過(guò)多久想要自己去證明時(shí)卻發(fā)現(xiàn)怎么都沒(méi)法補(bǔ)上證明中缺失的一環(huán)呢？

初中學(xué)習(xí)幾何證明的時(shí)候，你會(huì)不會(huì)傻到去背一個(gè)定理的證明？不會(huì)。你只會(huì)背結(jié)論。為什么？一方面，因?yàn)樽C明過(guò)程包含大量的細(xì)節(jié)。另一方面，證明的過(guò)程環(huán)環(huán)相扣，往往只需要注意其中關(guān)鍵的一兩步，便能夠自行推導(dǎo)出來(lái)。算法邏輯描述就好比定理，算法的證明的過(guò)程就好比定理的證明過(guò)程。但不幸的是，與數(shù)學(xué)里面大量簡(jiǎn)潔的基本結(jié)論不同，算法這個(gè)“結(jié)論”可不是那么好背的，許多時(shí)候，算法本身的邏輯就幾乎包含了與其證明過(guò)程等同的信息量，甚至算法邏輯本身就是證明過(guò)程（隨便翻開(kāi)一本經(jīng)典的算法書(shū)，看幾個(gè)經(jīng)典的教科書(shū)算法，你會(huì)發(fā)現(xiàn)算法邏輯和算法證明的聯(lián)系有多緊密）。于是我們又回到剛才那個(gè)問(wèn)題：你會(huì)去背數(shù)學(xué)證明么？既然沒(méi)人會(huì)傻到去背整個(gè)證明，又為什么要生硬地去背算法呢？

那么，不背就不背，去理解算法的證明如何？理解了算法的證明過(guò)程，便更有可能記住算法的邏輯細(xì)節(jié)，理解記憶嘛。然而，仍然不幸的是，絕大多數(shù)算法書(shū)在這方面做的實(shí)在糟糕，證明倒是給全了，邏輯也倒是挺嚴(yán)謹(jǐn)?shù)模墒撬坪鯖](méi)有作者能真正還原算法發(fā)明者本身如何得到算法以及算法證明的思維過(guò)程，按理說(shuō)，證明的過(guò)程應(yīng)該反映了這個(gè)思維過(guò)程，但是在下文關(guān)于霍夫曼編碼的例子中你會(huì)看到，其實(shí)飽受贊譽(yù)的CLRS和《Algorithms》不僅沒(méi)能還原這個(gè)過(guò)程，反而掩蓋了這個(gè)過(guò)程。

必須說(shuō)明的是，沒(méi)有哪位作者是故意這樣做的，但任何人在講解一個(gè)自己已經(jīng)理解了的東西的時(shí)候，往往會(huì)無(wú)意識(shí)地對(duì)自己的講解進(jìn)行“線性化”，例如證明題，如果你回憶一下高中做平面幾何證明題的經(jīng)歷，就會(huì)意識(shí)到，其實(shí)證明的過(guò)程是一個(gè)充滿了試錯(cuò)，聯(lián)想，反推，特例，修改問(wèn)題條件，窮舉等等一干“非線性”思維的，混亂不堪的過(guò)程，而并不像寫(xiě)在課本上那樣——引理1，引理2，定理1，定理2，一口氣直到最終結(jié)論。這樣的證明過(guò)程也許容易理解，但絕對(duì)不容易記憶。過(guò)幾天你就會(huì)忘記其中一個(gè)或幾個(gè)引理，其中的一步或幾步關(guān)鍵的手法，然后當(dāng)你想要回過(guò)頭來(lái)自己試著去證明的時(shí)候，就會(huì)發(fā)現(xiàn)卡在某個(gè)關(guān)鍵的地方，為什么會(huì)這樣？因?yàn)樽C明當(dāng)中并沒(méi)有告訴你為什么作者當(dāng)時(shí)會(huì)想到證明算法需要那么一個(gè)引理或手法，所以，雖說(shuō)看完證明之后，對(duì)算法這個(gè)結(jié)論而言你是知其所以然了，但對(duì)于算法的證明過(guò)程你卻還沒(méi)知其所以然。在我們大腦的記憶系統(tǒng)當(dāng)中，新的知識(shí)必須要和既有的知識(shí)建立聯(lián)系，才容易被回憶起來(lái)（《如何有效地學(xué)習(xí)與記憶》），聯(lián)系越多，越容易回憶，而一個(gè)天外飛仙似地引理，和我們既有的知識(shí)沒(méi)有半毛錢聯(lián)系，沒(méi)娘的孩子沒(méi)人疼，自然容易被遺忘。（為什么還原思維過(guò)程如此困難呢？我曾經(jīng)在知其所以然（一）里詳述）

正因?yàn)榻^大多數(shù)算法書(shū)上悲劇的算法證明過(guò)程，很多人發(fā)現(xiàn)證明本身也不好記，于是寧可選擇直接記結(jié)論。當(dāng)年我在數(shù)學(xué)系，考試會(huì)考證明過(guò)程，但似乎計(jì)算機(jī)系的考試考算法證明過(guò)程就是荒謬的？作為“工程”性質(zhì)的程序設(shè)計(jì)，似乎更注重使用和結(jié)果。但是如果是你需要在項(xiàng)目中自己設(shè)計(jì)一個(gè)算法呢？這種時(shí)候最起碼需要做的就是證明算法的正確性吧。我們面試的時(shí)候往往都會(huì)遇到一些算法設(shè)計(jì)問(wèn)題，我總是會(huì)讓?xiě)?yīng)聘者去證明算法的正確性，因?yàn)榧幢闶?strong>一個(gè)“看上去”正確的算法，真正需要證明起來(lái)往往發(fā)現(xiàn)并不是那么容易。

所以說(shuō)，絕大多數(shù)算法書(shū)在作為培養(yǎng)算法設(shè)計(jì)者的角度來(lái)說(shuō)是失敗的，比數(shù)學(xué)教育更失敗。大多數(shù)人學(xué)完了初中平面幾何都會(huì)做證明題（數(shù)學(xué)書(shū)不會(huì)要求你記住幾何所有的定理），但很多人看完了一本算法書(shū)還是一團(tuán)漿糊，不會(huì)證明一些起碼的算法，我們背了一坨又一坨結(jié)論，非但這些結(jié)論許多根本用不上，就連用上的那些也不會(huì)證明。為什么會(huì)出現(xiàn)這樣的差異？因?yàn)閿?shù)學(xué)教育的理想目的是為了讓你成為能夠發(fā)現(xiàn)新定理的科學(xué)家，而碼農(nóng)系的算法教育的目的卻更現(xiàn)實(shí)，是為了讓你成為能夠使用算法做事情的工程師。然而，事情真的如此簡(jiǎn)單么？如果真是這樣的話干脆連算法結(jié)論都不要背了，只要知道算法做的是什么事情，時(shí)空復(fù)雜度各是多少即可。

如果說(shuō)以上提到的算法難度（講解和記憶的難度）屬于Accidental Complexity的話，算法的另一個(gè)難處便是Essential Complexity了：算法設(shè)計(jì)。還是拿數(shù)學(xué)證明來(lái)類比（如果你看過(guò)《Introduction to Algorithms：A Creative Approach》就知道算法和數(shù)學(xué)證明是多么類似。），與單單只需證明相比，設(shè)計(jì)算法的難處在于，定理和證明都需要你去探索，尤其是前者——你需要去自行發(fā)現(xiàn)關(guān)鍵的那（幾）個(gè)定理，跟證明已知結(jié)論相比（已經(jīng)確定知道結(jié)論是正確的了，你只需要用邏輯來(lái)連接結(jié)論和條件），這件事情的復(fù)雜度往往又難上一個(gè)數(shù)量級(jí)。

一個(gè)有趣的事實(shí)是，算法的探索過(guò)程往往蘊(yùn)含算法的證明過(guò)程，理想的算法書(shū)應(yīng)該通過(guò)還原算法的探索過(guò)程，從而讓讀者不僅能夠自行推導(dǎo)出證明過(guò)程，同時(shí)還能夠具備探索新算法的能力。之所以這么說(shuō)，皆因?yàn)槲沂莻€(gè)懶人，懶人總夢(mèng)想學(xué)點(diǎn)東西能夠?qū)崿F(xiàn)以下兩個(gè)目的：

一勞永逸：程序員都知道“一次編寫(xiě)到處運(yùn)行”的好處，多省事啊。學(xué)了就忘，忘了又得學(xué)，翻來(lái)覆去浪費(fèi)生命。為什么不能看了一遍就再也不會(huì)忘掉呢？到底是教的不好，還是學(xué)得不好？

事半功倍：事實(shí)上，程序員不僅講究一次編寫(xiě)到處運(yùn)行，更講究“一次編寫(xiě)到處使用”（也就是俗稱的“復(fù)用”）。如果學(xué)一個(gè)算法所得到的經(jīng)驗(yàn)可以到處使用，學(xué)一當(dāng)十，推而廣之，時(shí)間的利用效率便會(huì)大大提高。究竟怎樣學(xué)習(xí)，才能夠使得經(jīng)驗(yàn)的外推（extrapolate）效率達(dá)到最大呢？

想要做到這兩點(diǎn)就必須盡量從知識(shí)樹(shù)的“根節(jié)點(diǎn)”入手，雖然這是一個(gè)美夢(mèng)，例如數(shù)學(xué)界尋找“根節(jié)點(diǎn)”的美夢(mèng)由來(lái)已久（《跟波利亞學(xué)解題》的“一點(diǎn)歷史”小節(jié)），但哥德?tīng)栆粋€(gè)證明就讓美夢(mèng)成了泡影（《永恒的金色對(duì)角線》））；但是，這并不阻止我們?nèi)ふ腋邔拥墓?jié)點(diǎn)——更具普適性的解題原則和方法。所以，理想的算法書(shū)或者算法講解應(yīng)該是從最具一般性的思維法則開(kāi)始，順理成章地推導(dǎo)出算法，這個(gè)過(guò)程應(yīng)該盡量還原一個(gè)”普通人“思考的過(guò)程，而不是讓人看了之后覺(jué)得”這怎么可能想到呢？

以本文上篇提到的霍夫曼編碼為例，第一遍看霍夫曼編碼的時(shí)候是在本科，只看了算法描述，覺(jué)得挺直觀的，過(guò)了兩年，忘了，因?yàn)椴恢罏槭裁匆褍蓚€(gè)節(jié)點(diǎn)的頻率加在一起看做單個(gè)節(jié)點(diǎn)——一件事情不知道“為什么”就會(huì)記不牢，知道了“為什么”的話便給這件事情提供了必然性。不知道“為什么”這件事情便可此可彼，我們的大腦對(duì)于可此可彼的事情經(jīng)常會(huì)弄混，它更容易記住有理有據(jù)的事情（從信息論的角度來(lái)說(shuō)，一件必然的事情概率為1，信息量為0，而一件可此可彼的事情信息量則是大于0的）。第二遍看是在工作之后，終于知道要看證明了，拿出著名的《Algorithms》來(lái)看，邊看邊點(diǎn)頭，覺(jué)得講得真好，一看就理解了為什么要那樣來(lái)構(gòu)造最優(yōu)編碼樹(shù)。可是沒(méi)多久，又給忘了！這次忘了倒不是忘了要把兩個(gè)節(jié)點(diǎn)的頻率加起來(lái)算一個(gè)，而是忘了為什么要這么做，因?yàn)楫?dāng)時(shí)沒(méi)有弄清霍夫曼為什么能夠想到為什么應(yīng)該那樣來(lái)構(gòu)造最優(yōu)編碼樹(shù)。結(jié)果只知其一不知其二。

必須說(shuō)明的是，如果只關(guān)心算法的結(jié)論（即算法邏輯），那么理解算法的證明就夠了，光背算法邏輯難記住，理解了證明會(huì)容易記憶得多。但如果也想不忘算法的證明，那么不僅要理解證明，還要理解證明背后的思維，也就是為什么背后的為什么。后者一般很難在書(shū)和資料上找到，唯有自己多加揣摩。為什么要費(fèi)這個(gè)神？只要不會(huì)忘記結(jié)論不就結(jié)了嗎？取決于你想做什么，如果你想真正弄清算法設(shè)計(jì)背后的思想，不去揣摩算法原作者是怎么想出來(lái)的是不行的。

回到霍夫曼編碼問(wèn)題，我們首先看一看《Algorithms》上是怎么講的：

首先它給出了一棵編碼樹(shù)的cost function：

cost of tree = Σ freq(i) * depth(i)

這個(gè)cost function很直白，就是把編碼的定義復(fù)述了一遍。但是接下來(lái)就說(shuō)了：

There is another way to write this cost function that is very helpful.Although we are only given frequencies for the leaves, we can define the frequency of any internal node to be the sum of the frequencies of its descendant leaves; this is, after all, the number of times the internal node is visited during encoding or decoding…

接著就按照這個(gè)思路把cost function轉(zhuǎn)換了一下：

The cost of a tree is the sum of the frequencies of all leaves and internal nodes, except the root.

然后就開(kāi)始得出算法邏輯了：

Thefirst formulationof the cost function tells us that thetwo symbols with the smallest frequencies must be at the bottom of the optimal tree, as children of the lowest internal node (this internal node has two children since the tree is full). Otherwise, swapping these two symbols with whatever is lowest in the tree would improve the encoding.

This suggests that we start constructing the tree greedily: find the two symbols with the smallest frequencies, say i and j, and make them children of a new node, which then has frequency fi + fj. To keep the notation simple, let’s just assume these are f1 and f2. By thesecond formulationof the cost function, any tree in which f1 and f2 are sibling-leaves has cost f1 + f2 plus the cost for a tree with n – 1 leaves of frequencies (f1 + f2), f3, f4, .., fn.The latter problem is just a smaller version of the one we started with.

讀到這里我想大多數(shù)人有兩種反應(yīng)：

覺(jué)得理所當(dāng)然。

覺(jué)得恍然大悟。

因?yàn)槲耶?dāng)時(shí)也是這么覺(jué)得的。可是后來(lái)當(dāng)我發(fā)現(xiàn)自己無(wú)法從頭證明一遍的時(shí)候，我知道肯定是理解的不夠深刻。如果理解的夠深刻，那么基本上是不會(huì)忘掉的。

如果看完霍夫曼編碼這樣一個(gè)簡(jiǎn)短證明你覺(jué)得順理成章，一切都挺顯然，那就壞了，即便是看上去最基本的性質(zhì)也往往實(shí)際上沒(méi)那么顯然。“逢山開(kāi)路，遇水架橋”在我們今天看來(lái)是無(wú)比顯然的事實(shí)，但是試想在沒(méi)有橋的遠(yuǎn)古時(shí)代，一個(gè)原始人走到一條湍急的河流前，他會(huì)怎么想，他又能有什么法子呢？這是個(gè)他從來(lái)沒(méi)有遇見(jiàn)過(guò)的問(wèn)題。如果后來(lái)有一天，他路過(guò)另外一條小溪，看到小溪上有一截被閃電劈斷的枯樹(shù)，于是他踏著樹(shù)干走過(guò)了小溪，并意識(shí)到“樹(shù)橫過(guò)河面”可以達(dá)到“過(guò)河”這個(gè)目的，這就將條件和目的建立了直接的聯(lián)系（事實(shí)上，是自然界展示了這個(gè)聯(lián)系，我們的原始人只是記住了這個(gè)聯(lián)系）。后來(lái)他又路過(guò)那條河流，他尋思如何達(dá)到“過(guò)河”這個(gè)目的的時(shí)候，忽然意識(shí)到在他的記憶中已經(jīng)遇到過(guò)需要達(dá)成同樣目的的時(shí)候了，那個(gè)時(shí)候的條件是“樹(shù)橫過(guò)河面”，于是問(wèn)題便歸結(jié)為如何滿足這個(gè)“樹(shù)橫過(guò)河面”的條件，而后一個(gè)問(wèn)題就簡(jiǎn)單多了。（事實(shí)上波利亞在他的著作《How to Solve it》中舉的正是這么個(gè)例子）

為什么那么多的算法書(shū)，就看不到有一本講得好的？因?yàn)槲覀兦蠼鈫?wèn)題過(guò)程中的思維步驟太容易被自己當(dāng)作“顯然”的了，但除了我們天生就會(huì)的認(rèn)知模式（聯(lián)系，類比），沒(méi)有什么是應(yīng)該覺(jué)得顯然的，試錯(cuò)是我們天生就會(huì)的思維法則么？是的，但是可供嘗試的方案究竟又是怎么來(lái)的呢？就拿上面的例子來(lái)說(shuō)，一個(gè)從沒(méi)有見(jiàn)過(guò)枯樹(shù)干架在小溪上的原始人，怎么知道用樹(shù)架橋是一種可選的方案呢？俗話說(shuō)巧婦難為無(wú)米之炊啊。我們大腦的神經(jīng)系統(tǒng)會(huì)的是將目的和條件聯(lián)系起來(lái)，第一次原始人遇到小溪過(guò)不去，大腦中留下了一個(gè)未實(shí)現(xiàn)的目的，后來(lái)見(jiàn)到小溪上的樹(shù)干，忽然意識(shí)到樹(shù)干是實(shí)現(xiàn)這個(gè)目的的條件，兩者便聯(lián)系起來(lái)了，因此問(wèn)題就規(guī)約為如何架樹(shù)干了。

回到《Algorithms》中的證明上，這個(gè)看似簡(jiǎn)潔明了的證明其實(shí)有幾處非常不顯然的地方，甚至不嚴(yán)謹(jǐn)?shù)牡胤剑@些地方也正是你過(guò)段時(shí)間之后試圖自己證明的話會(huì)發(fā)現(xiàn)卡住的地方：

作者輕飄飄地就給出了cost function的另外一種關(guān)鍵的描述，而對(duì)于如何發(fā)現(xiàn)這種描述卻只是一語(yǔ)帶過(guò)："There is another way to write this cost function that is very helpful..we can define the frequency of any internal node to be the sum of the frequencies of its descendant leaves“這其實(shí)就是我常常痛恨的“我們考慮…”，這里作者其實(shí)就是在說(shuō)”讓我們考慮下面這樣一種奇妙的轉(zhuǎn)換“，可是怎么來(lái)的卻不說(shuō)。但必須承認(rèn)，《Algorithms》的作者還是算厚道的，因?yàn)楹竺嫠稚晕⒔忉屃艘幌拢骸皌his is, after all, the number of times the internal node is visited during encoding or decoding…”這個(gè)解釋就有點(diǎn)讓人恍然大悟了，但是千萬(wàn)別忘了，這種恍然大悟是一種錯(cuò)覺(jué)，你還是沒(méi)明白為什么他會(huì)想到這一點(diǎn)。這就像是作者對(duì)你說(shuō)“仔細(xì)觀察問(wèn)題條件，我們?nèi)菀装l(fā)現(xiàn)這樣一種奇妙的性質(zhì)..”，怎么個(gè)“仔細(xì)”法？憑什么我自己“觀察”半天就是發(fā)現(xiàn)不了呢？霍夫曼本人難道也是死死盯著問(wèn)題“觀察”了一學(xué)期然后就“發(fā)現(xiàn)”了么？我們有理由相信霍夫曼肯定嘗試了各種各樣的方法，作出了各種各樣的努力，否則當(dāng)年Shannon都沒(méi)搞定的這個(gè)問(wèn)題花了他一學(xué)期，難道他在這個(gè)學(xué)期里面大腦就一片空白（或者所有的嘗試全都是完全不相干的徒勞），然后到學(xué)期末尾忽然“靈光一現(xiàn)”嗎？

如果“仔細(xì)觀察”:)，我們會(huì)發(fā)現(xiàn)兩個(gè)cost function表達(dá)中frequency的概念有微妙的差異，在第一個(gè)cost function中，只有葉子節(jié)點(diǎn)有frequency，而這個(gè)frequency必須和葉子節(jié)點(diǎn)的深度相乘。而在第二個(gè)cost function中，內(nèi)部節(jié)點(diǎn)也具有了frequency，可是所有節(jié)點(diǎn)的“frequency”忽然全都不跟深度相乘了。frequency的不同含義令人困惑。

作者提到：第一個(gè)cost function告訴我們頻率最低的兩個(gè)節(jié)點(diǎn)必然處于最優(yōu)編碼樹(shù)的底端，作為最低內(nèi)部節(jié)點(diǎn)的兩個(gè)子節(jié)點(diǎn)。這是一個(gè)不嚴(yán)謹(jǐn)?shù)恼f(shuō)法，從前文給出的條件和性質(zhì)，只能推導(dǎo)出編碼樹(shù)的最底層必然能找到頻率最低的兩個(gè)節(jié)點(diǎn)，但它們未必一定要是兄弟節(jié)點(diǎn)，如果樹(shù)的最底層不止能容納兩個(gè)節(jié)點(diǎn)的話它們就可以有不同的父節(jié)點(diǎn)。“我們不妨考慮”這樣一個(gè)例子：對(duì)A,B,C,D四個(gè)字母進(jìn)行編碼，假設(shè)它們的頻率分別是1， 1， 2， 2。這個(gè)時(shí)候我們可以構(gòu)造如下圖所示的兩棵樹(shù)，兩棵樹(shù)的cost都是12，都是最優(yōu)的。但其中一棵樹(shù)中，兩個(gè)頻率最低的節(jié)點(diǎn)并非兄弟。

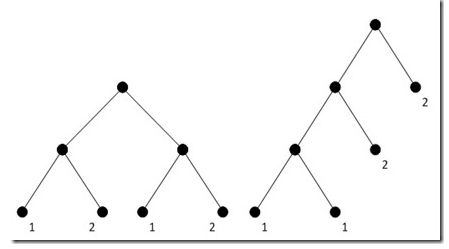
為什么要提到上面這幾點(diǎn)不顯然和不嚴(yán)謹(jǐn)?shù)牡胤剑驗(yàn)橹灰?dāng)你看到算法書(shū)上出現(xiàn)不顯然和不嚴(yán)謹(jǐn)?shù)牡胤剑旧暇鸵馕吨髡咂鋵?shí)跳過(guò)了關(guān)鍵的思維步驟。

不幸的是《Algorithms》這本書(shū)里面講霍夫曼編碼已經(jīng)算是講的好的了，如果你翻開(kāi)著名的CLRS，看一看當(dāng)中是怎么證明的，你就知道我說(shuō)的什么意思了。有時(shí)候這些證明是如此的企圖追求formal和嚴(yán)謹(jǐn)，一上來(lái)就定義符號(hào)一大摞，讓人看了就想吐。

說(shuō)了這么多，有沒(méi)有可能把霍夫曼編碼講的更好呢？前面說(shuō)過(guò)，霍夫曼編碼我記了又忘，忘了又記，好幾次了，有一次終于煩了，心想如果要自己去證明，會(huì)怎么去證，那個(gè)時(shí)候我已經(jīng)忘了《Algorithms》里面怎么講的了。所以我得從頭來(lái)起，首先，對(duì)于算法問(wèn)題，有一個(gè)一般性原則是，先看一看解空間的構(gòu)成。尤其是對(duì)于搜索問(wèn)題（最優(yōu)化問(wèn)題可以看做搜索問(wèn)題的一個(gè)特例），這一點(diǎn)尤其重要。霍夫曼編碼的可能的編碼樹(shù)是有窮的，如果窮舉所有的編碼樹(shù)，然后找到那棵代價(jià)最小的，這種方法至少是可行的，有了可行的方法（即便是窮舉）至少讓我們內(nèi)心感到踏實(shí)。

接下來(lái)便是提高搜尋效率的問(wèn)題。而提高搜尋效率的關(guān)鍵（同樣也是一個(gè)一般性原則），便是盡量去尋找問(wèn)題條件能夠推導(dǎo)出來(lái)的性質(zhì)，****然后利用這些性質(zhì)去避免不必要的搜尋，只要你學(xué)過(guò)二分搜索就應(yīng)該理解這個(gè)一般性原則：二分搜索的效率之所以高于“窮搜”（O(n)），便是因?yàn)樗昧藛?wèn)題中的性質(zhì)（有序）來(lái)避免了不必要的搜尋。有時(shí)候這個(gè)性質(zhì)甚至可以直接將時(shí)間降為O(1)，例如在一個(gè)有序數(shù)組中尋找出現(xiàn)次數(shù)大于n/2的數(shù)（假設(shè)該數(shù)存在），利用“該數(shù)一定出現(xiàn)在數(shù)組正中間”這個(gè)性質(zhì)，我們直接就避免了所有的計(jì)算。

不過(guò)，話雖如此，有時(shí)候這些性質(zhì)并不是那么“顯然”的，需要對(duì)問(wèn)題進(jìn)行深入的折騰才能有可能發(fā)現(xiàn)。第三個(gè)一般原則：如果你要搜尋的元素是某個(gè)滿足特定條件的元素（例如尋找最優(yōu)解的時(shí)候，“最優(yōu)”的定義就是這個(gè)“特定條件”），那么可以“倒過(guò)來(lái)推”（數(shù)學(xué)證明常用手法，結(jié)論當(dāng)條件使），即假設(shè)你已經(jīng)找到了你要找的元素，那么能得出哪些結(jié)論，每一個(gè)結(jié)論都是最優(yōu)解的一個(gè)必要條件，而每一個(gè)必要條件都能夠幫助你避免不必要的搜尋，因?yàn)槟阒灰l(fā)現(xiàn)某個(gè)候選解不滿足某個(gè)必要條件，就可以立即將其丟棄，前面提到的尋找出現(xiàn)次數(shù)大于n/2的例子是一個(gè)極端情況，我們得出的必要條件導(dǎo)致我們可以直接丟棄除中點(diǎn)元素之外的一切其他元素，再例如如果有人叫你尋找有序數(shù)組中最小元素，你會(huì)毫不猶豫地把該數(shù)組頭尾元素中較小的那個(gè)給他，因?yàn)槟阒馈叭绻莻€(gè)最小元素存在，那么它必然位于頭尾”——這個(gè)必要條件直接允許你丟棄掉n-2個(gè)候選解。

回到霍夫曼編碼問(wèn)題，按照這個(gè)原則，我們會(huì)去假設(shè)已經(jīng)得到了最優(yōu)編碼樹(shù)，那么我們能夠發(fā)現(xiàn)關(guān)于它的什么性質(zhì)呢？這里又要提到另一個(gè)適用于很多最優(yōu)化問(wèn)題的原則（前面提到的原則適用于一般性搜索問(wèn)題），所謂最優(yōu)解，就是說(shuō)比其他所有解都要更好，雖然這句話聽(tīng)上去像是廢話，但是它的一個(gè)直接推論——比與它鄰近的所有候選解都要好——就是一個(gè)非常有用的，不是廢話的性質(zhì)了。學(xué)過(guò)微積分的都知道，光滑函數(shù)的最值點(diǎn)必然是大（小）于其鄰域內(nèi)的所有點(diǎn)的，然后再根據(jù)這個(gè)就自然推出該點(diǎn)的一階導(dǎo)數(shù)（切線斜率）必然為0的性質(zhì)，這個(gè)性質(zhì)（必要條件）讓我們直接省掉了去整個(gè)區(qū)間內(nèi)搜索的麻煩，從而可以直接鎖定有限幾個(gè)候選解。那么，既然我們說(shuō)最優(yōu)霍夫曼樹(shù)一定比它“附近”的樹(shù)更好，我們就想看看，怎么來(lái)找到它附近的樹(shù)。我們知道要從一個(gè)點(diǎn)到它附近，往往是對(duì)這個(gè)點(diǎn)進(jìn)行一些調(diào)整，例如N+1是到達(dá)附近的另一個(gè)整數(shù)。霍夫曼樹(shù)是一棵樹(shù)，所以對(duì)這棵樹(shù)的所有的一次“改動(dòng)”（或“折騰”）都能夠到達(dá)與它的“改動(dòng)”距離為1的點(diǎn)（是不是想起“編輯距離”這個(gè)概念），怎么改動(dòng)呢？最符合直覺(jué)的（雖然并不是唯一的）改動(dòng)便是把葉子節(jié)點(diǎn)進(jìn)行互換。

于是我們得到一個(gè)重要的推論：

在最優(yōu)霍夫曼樹(shù)中，無(wú)論互換哪兩個(gè)葉子節(jié)點(diǎn)，得到的樹(shù)都變得更“差”。（嚴(yán)格來(lái)說(shuō)是不會(huì)變得更“好”，因?yàn)樽顑?yōu)樹(shù)未必唯一）

這個(gè)性質(zhì)看上去有點(diǎn)像廢話，值得費(fèi)這么多事么？值得。因?yàn)殡m然前文說(shuō)了很多，但都是大多數(shù)人大腦里面既有的，一般性的法則，前面說(shuō)過(guò)，如果我們能夠從我們已經(jīng)掌握的一般法則出發(fā)來(lái)推導(dǎo)出問(wèn)題的解，那么記憶負(fù)擔(dān)是最小的，因?yàn)檫@里面用到的所有法則我們都很清楚，也知道怎么一步步往下走。

上面這個(gè)性質(zhì)究竟意味著什么呢？如果你假設(shè)這兩個(gè)葉子節(jié)點(diǎn)的頻率為f1和f2，深度為d1和d2，互換它們的時(shí)候，其他葉子節(jié)點(diǎn)的cost保持不變，令為常量C，那么互換前總cost為C+f1d1+f2d2，互換后為C+f1d2+f2d1，既然互換之后的樹(shù)一定更”差“那么就是說(shuō)f1d1+f2d2 < f1d2 + f2d1，簡(jiǎn)單變換一下就得到結(jié)論：f1(d1-d2)f2，如果d1>d2，那么f1必然

有了這個(gè)結(jié)論之后，我們便能夠?qū)ψ顑?yōu)霍夫曼樹(shù)的構(gòu)建走出確定性的一步，即，將頻率最低的兩個(gè)葉子節(jié)點(diǎn)放在最底層。別小看這一步，這一步已經(jīng)排除了大量的可能性。這里，我們?nèi)菀滓婚_(kāi)始天真地覺(jué)得最底層只有這兩個(gè)葉子節(jié)點(diǎn)，于是它們擁有共同父節(jié)點(diǎn)，這樣一來(lái)霍夫曼樹(shù)的整個(gè)拼圖便已經(jīng)拼好了一個(gè)小小的角落。

然后我們會(huì)發(fā)現(xiàn)，要是它們不是兄弟怎么辦呢？這里提到另一個(gè)一般原則——歸約。不是兄弟的情況能否歸約為是兄弟的情況？反正我們要求的是一個(gè)最優(yōu)解，而不是所有的最優(yōu)解，我們只需證明，如果當(dāng)這兩個(gè)最低頻率的葉子不是兄弟的時(shí)候的確存在著某棵最優(yōu)霍夫曼樹(shù)，那么通過(guò)交換它們各自的兄弟，從而讓這兩個(gè)葉子團(tuán)聚之后，修改后的樹(shù)仍然是最優(yōu)的就可以了。事實(shí)情況也的確如此，證明非常直接——既然這里涉及到的所有4個(gè)節(jié)點(diǎn)都在最底層同一個(gè)高度上，那么互相交換的時(shí)候不會(huì)改變他們?nèi)魏我粋€(gè)人的深度值，所以總cost不會(huì)改變。

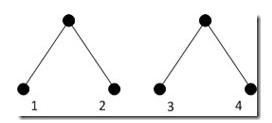
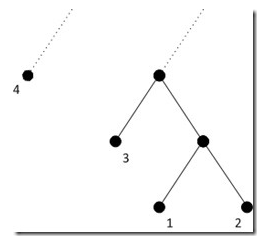
但是接下來(lái)我們犯了難，整個(gè)樹(shù)的一個(gè)小小的櫻桃狀的局部是確定下來(lái)了，接下來(lái)怎么辦呢？一個(gè)最自然的思路就是考慮第三小的葉子，因?yàn)榍懊嬲f(shuō)了，元素頻率越低就越位于樹(shù)的底部嘛。第三小的葉子有兩種可能的歸屬，一是跟最小的兩個(gè)葉子同樣位于最底層（這不會(huì)違反我們前面得到的推論），這個(gè)時(shí)候第三小的葉子的兄弟葉子肯定是第四小的葉子，如下圖：

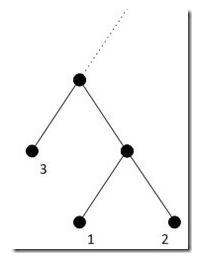
另一種歸屬就是往上一層去（注意，一旦第三小的葉子往上去了一層，那么剩下的所有葉子都必須至少在這個(gè)層以上），往上一層去了之后，它的兄弟是誰(shuí)呢？不妨將它和剛才第一第二葉子的父節(jié)點(diǎn)結(jié)為兄弟（前面證明過(guò)，同層之前節(jié)點(diǎn)互換不會(huì)改變編碼的cost），如下圖：

可是現(xiàn)在問(wèn)題出現(xiàn)了：雖然第一步構(gòu)建（最小的兩個(gè)葉子）是確定的，但是到了第二步擺在我們面前的就有兩個(gè)選擇了，到底選擇哪個(gè)呢？一個(gè)辦法就是把兩種選擇都記下來(lái)，然后繼續(xù)往下走。可是別小看兩種選擇，接下去每一步都有兩種選擇的話就變成指數(shù)復(fù)雜度了。所以現(xiàn)在我們便有了動(dòng)機(jī)回頭看一看，看問(wèn)題中是否有什么沒(méi)有發(fā)現(xiàn)的性質(zhì)能夠幫助我們?cè)倥懦羝渲幸粋€(gè)選擇。理想情況下如果每一步都是必然的，確定的，那么N步我們就可以構(gòu)建出整棵樹(shù)，這是我們希望看到的，抱著這個(gè)良好的愿望，我們仔細(xì)觀察上面兩種構(gòu)型，一個(gè)自然而然的問(wèn)題是：這兩種構(gòu)型都有潛質(zhì)成為最優(yōu)解嗎？如果我們能夠證明其中一種構(gòu)型不能成為最優(yōu)解那該多好？就省事多了嘛。這里引入另一個(gè)一般性的解題法則：特例。我們的大腦喜歡具體的東西，在特例中折騰和觀察會(huì)方便的多。

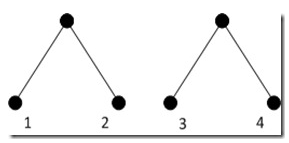
上面這個(gè){1, 2, 3, 4}的例子就是個(gè)很好的特例，如圖（注：圖中節(jié)點(diǎn)旁的數(shù)字一概為頻率值，而非編號(hào)）：

多加折騰一番也許我們不難發(fā)現(xiàn)，如果將1，2及其父節(jié)點(diǎn)跟葉子4進(jìn)行交換（注意：交換的時(shí)候1，2也被一同帶走了，因?yàn)榉凑?，2兩個(gè)節(jié)點(diǎn)已確定是好兄弟永遠(yuǎn)不會(huì)分家了，折騰的時(shí)候只能作為一個(gè)整體移動(dòng)，所以這里也可以說(shuō)是交換子樹(shù)），那么樹(shù)的編碼將會(huì)變得更優(yōu)，因?yàn)檫@樣一次交換會(huì)將1和2的深度+1，意味著整棵樹(shù)的代價(jià)+3，而同時(shí)會(huì)將葉子4的深度-1，也就是說(shuō)整棵樹(shù)的代價(jià)-4，總體上整棵樹(shù)的代價(jià)就是+3-4=-1（注意，在計(jì)算的時(shí)候我們只需考慮被交換的局部，因?yàn)闃?shù)的其他部分的代價(jià)保持不變）。如下圖：

這個(gè)交換啟發(fā)了我們，其實(shí)前面一開(kāi)始說(shuō)的交換兩個(gè)葉子節(jié)點(diǎn)可以推廣為交換內(nèi)部節(jié)點(diǎn)和葉子節(jié)點(diǎn)，然后很快我們就會(huì)意識(shí)到其實(shí)可以推廣到交換任意兩個(gè)節(jié)點(diǎn)。（注意，當(dāng)我們說(shuō)交換內(nèi)部節(jié)點(diǎn)的時(shí)候，其實(shí)是連同該內(nèi)部節(jié)點(diǎn)作為局部根節(jié)點(diǎn)的整個(gè)子樹(shù)都交換過(guò)去）于是前面我們的推論就可以推廣為：

在最優(yōu)霍夫曼樹(shù)中，無(wú)論互換哪兩個(gè)節(jié)點(diǎn)，得到的樹(shù)都變得更“差”（交換內(nèi)部節(jié)點(diǎn)則是連同該內(nèi)部節(jié)點(diǎn)作為局部根的子樹(shù)一同帶走）

這個(gè)推論很容易理解，只不過(guò)是多增加了一種“編輯”最優(yōu)霍夫曼樹(shù)的方法罷了（記住最優(yōu)霍夫曼樹(shù)無(wú)論怎么“編輯”都不會(huì)變得更“好”，包括“交換子樹(shù)”這種“編輯”），我們前面沒(méi)有想到這種“編輯”方法是因?yàn)樗荒敲达@然，而且當(dāng)時(shí)我們已經(jīng)想到一種最直接的“編輯”方法了，即交換葉子，就容易順著那個(gè)思路一直走下去，直到我們發(fā)現(xiàn)必須尋找新的性質(zhì)，才回過(guò)頭來(lái)看看有沒(méi)有其他法子。

當(dāng)然，并不排除一開(kāi)始就想到這種推廣的可能性，問(wèn)題求解的過(guò)程并不是這么線性的，如果我們習(xí)慣了推而廣之的思維，也許一下就能想到這個(gè)推廣來(lái)。類似的，也不排除從另一種思路出發(fā)想到這種推廣的可能性。所以這里只是可能的思維軌跡中的一種，重點(diǎn)在于其中并沒(méi)有某處忽然出現(xiàn)一個(gè)不知從哪里冒出來(lái)的，神啟一般的結(jié)論。

剛才提到，構(gòu)造最優(yōu)樹(shù)的第二步是考慮第三小的葉子，但也有另一種常見(jiàn)的思維：考慮到第一步（即選取頻率最小的兩個(gè)葉子）所做的事情是從N個(gè)葉子中選擇兩個(gè)黏在一起作為兄弟，那么也許對(duì)于一些人來(lái)說(shuō)自然而然的第二步就是試圖繼續(xù)選取兩個(gè)節(jié)點(diǎn)黏在一起作為兄弟（注意這里不僅可以選擇葉子，也可以選擇已經(jīng)生成的內(nèi)部節(jié)點(diǎn)），然后依次類推來(lái)拼完整棵樹(shù)。按照這一思路，第二步的選項(xiàng)仍然還是集中在第三小的葉子上，因?yàn)檫@個(gè)選擇要么是讓第三第四小的葉子結(jié)拜為兄弟，要么是讓最小兩個(gè)葉子的父節(jié)點(diǎn)和第三小的葉子結(jié)拜。

回到剛才我們的推論：在最優(yōu)霍夫曼樹(shù)中，無(wú)論互換哪兩個(gè)節(jié)點(diǎn)，得到的樹(shù)都變得更“差”（交換內(nèi)部節(jié)點(diǎn)則是連同該內(nèi)部節(jié)點(diǎn)作為局部根的子樹(shù)一同帶走） 。根據(jù)這個(gè)推論我們?nèi)菀子?jì)算出，在最優(yōu)霍夫曼樹(shù)當(dāng)中，兩個(gè)內(nèi)部節(jié)點(diǎn)n1和n2，如果n1比n2更深，那么n1下面的所有葉子的頻率之和必然要小于n2下面所有葉子的頻率之和。如果交換的是一個(gè)內(nèi)部節(jié)點(diǎn)和一個(gè)葉子節(jié)點(diǎn)，則道理是類似的。這個(gè)性質(zhì)的證明和上面的類似，就不贅述了。

這個(gè)性質(zhì)暗示了一個(gè)重要的推廣結(jié)論：如果我們把每個(gè)內(nèi)部節(jié)點(diǎn)的所有葉子的頻率之和標(biāo)在它旁邊，那么整棵樹(shù)的每個(gè)節(jié)點(diǎn)便都有了一個(gè)數(shù)值，這個(gè)數(shù)值遵循統(tǒng)一的規(guī)律：即越往深層越小。這就意味著，我們剛才的二選一困境有辦法了！當(dāng)我們將最小的兩個(gè)葉子f1和f2合并的時(shí)候，生成了一個(gè)新的節(jié)點(diǎn)M，這個(gè)節(jié)點(diǎn)有一個(gè)數(shù)字（為兩個(gè)葉子的頻率之和f1+f2），根據(jù)上面的推論，這個(gè)數(shù)字f1+f2跟所有頻率一同，遵循最小的在最底層的原則，所以我們下一步必須在剩下的那些互相之間關(guān)系待確定的節(jié)點(diǎn)（葉子節(jié)點(diǎn)和內(nèi)部節(jié)點(diǎn)）之中，即{(f1 + f2), f3, f4}里面選擇最小的兩個(gè)數(shù)字結(jié)合成兄弟（由于f1和f2這兩個(gè)節(jié)點(diǎn)已經(jīng)鐵板釘釘結(jié)為整體了，所以從集合里面可以看做移除）。到這里，我們就發(fā)現(xiàn)遞歸已經(jīng)出現(xiàn)了，接下去的過(guò)程對(duì)于絕大多數(shù)人應(yīng)該就真的很顯然了。

以上的解釋，比《Algorithms》更簡(jiǎn)短嗎？顯然不是。反而要長(zhǎng)得多（其實(shí)真正的思維過(guò)程比這要更長(zhǎng)，因?yàn)橹虚g還會(huì)涉及各種不成功的嘗試）。但是它比《Algorithms》當(dāng)中的版本更不容易被忘記，因?yàn)槠渲嘘P(guān)鍵的思維拐點(diǎn)并不是毫無(wú)來(lái)由的，而是從你已經(jīng)熟知的，或者說(shuō)雖然不知道，但容易理解的一般性解題法則出發(fā)自然推導(dǎo)出來(lái)的，所以你基本上不需要記憶什么東西，因?yàn)槟阈枰浀囊呀?jīng)在你腦海中了。

在上面的證明過(guò)程中，還有一個(gè)不像看上去那么顯然的事情：在我們尋找最優(yōu)霍夫曼樹(shù)的時(shí)候，我們?cè)?jīng)試圖去比較假想的最優(yōu)樹(shù)和它的“臨近”的樹(shù)，從而去探索最優(yōu)樹(shù)的性質(zhì)。但是，究竟什么是臨近的樹(shù)？在前面的講解中，我們說(shuō)如果交換A和B這兩個(gè)葉子節(jié)點(diǎn)，便得到一顆不同的樹(shù)，可以看做和原樹(shù)的“編輯距離”為1的樹(shù)。但是，真的這么顯然么？難道除了交換葉子的位置，就沒(méi)有其他辦法去“折騰”這棵樹(shù)了？后來(lái)我們看到，可以交換子樹(shù)而不僅僅是葉子，而交換子樹(shù)讓我們得到了至關(guān)重要的推論。此外，如果不是交換，而是像AVL樹(shù)那樣“旋轉(zhuǎn)”呢？說(shuō)到底，二叉樹(shù)是一個(gè)離散的東西，并不像連續(xù)值那樣，天生就有“距離”這個(gè)概念，如果我們離散而孤立地去看待所有的樹(shù)，那么沒(méi)有什么臨近不臨近的，臨近本是一個(gè)距離的概念，除非我們定義樹(shù)和樹(shù)之間的距離函數(shù)，才能說(shuō)臨近與否，而距離函數(shù)怎么定義才是“顯然”的呢？

還有，其實(shí)以上只是試圖給出最優(yōu)霍夫曼樹(shù)的證明的一個(gè)更自然的過(guò)程，而當(dāng)年霍夫曼面臨這個(gè)問(wèn)題的時(shí)候根本還沒(méi)有人想到要用二叉樹(shù)呢！更不要說(shuō)在二叉樹(shù)的前提之下進(jìn)行證明了。根據(jù)wikipedia的介紹，霍夫曼同學(xué)（當(dāng)年還在讀Ph.D，所以的確是“同學(xué)”，而這個(gè)問(wèn)題是坑爹的導(dǎo)師Robert M. Fano給他們作為大作業(yè)的，F(xiàn)ano自己和Shannon合作給出了一個(gè)suboptimal的編碼方案，為得不到optimal的方案而寢食難安，情急之下便死馬當(dāng)活馬醫(yī)扔給他的學(xué)生們了）當(dāng)年為這個(gè)問(wèn)題憔悴了一個(gè)學(xué)期，最后就快到deadline的時(shí)候“忽然”想到二叉樹(shù)這個(gè)等價(jià)模型，然后在這個(gè)模型下三下五除二就搞定了一篇流芳千古的論文，超越了其導(dǎo)師。

最后說(shuō)兩個(gè)有趣的現(xiàn)象：也許很多人會(huì)覺(jué)得，越是大師來(lái)寫(xiě)入門教科書(shū)越是好，其實(shí)很多時(shí)候并非如此，尤其是在算法設(shè)計(jì)和數(shù)學(xué)領(lǐng)域，往往越是在其中浸淫久了越是難寫(xiě)出貼近初學(xué)者的書(shū)，因?yàn)榇罅繉?duì)初學(xué)者來(lái)說(shuō)一點(diǎn)都不顯然的事情在他看來(lái)已經(jīng)是“不假思索”了，成了他的內(nèi)隱記憶，尤其是當(dāng)他想要和你解釋一個(gè)復(fù)雜的東西的時(shí)候你就會(huì)發(fā)現(xiàn)他會(huì)常常邏輯跳躍，滿嘴跑術(shù)語(yǔ)，根本沒(méi)有意識(shí)到別人對(duì)有些術(shù)語(yǔ)和隱含的邏輯根本沒(méi)有像他那樣的理解。

最適合將一個(gè)東西講給別人聽(tīng)的時(shí)候并不是等懂了很多年以后，而是剛剛弄懂的時(shí)候，這個(gè)時(shí)候從不懂到懂的差別記憶還非常鮮明，能夠清清楚楚地記得到底是哪些關(guān)鍵的地方是最折磨人的，也最能夠站在不懂者的角度來(lái)思考問(wèn)題。像波利亞這樣，成了大師還能夠站在不懂者角度去換位思考的，可以說(shuō)是鳳毛麟角。所以說(shuō)前Amazon CAO（首席算法官）的《Introduction to Algorithms: a Creative Approach》絕對(duì)是本罕見(jiàn)的好算法書(shū)）

知其所以然（一）里面曾經(jīng)提到，要弄清來(lái)龍去脈，最好去看看原始作者是怎么想的，可是正如上文所說(shuō)，即便是最初的發(fā)明者，在講述的時(shí)候也會(huì)有意無(wú)意地“線性化”，我就去查看了霍夫曼最初的論文，那叫一個(gè)費(fèi)解，不信你可以自己看看(PDF)。

可以歸約為搜索算法的問(wèn)題（非常多）一般來(lái)說(shuō)相對(duì)還是有一些頭緒的，因?yàn)樗阉骺臻g一般還比較容易界定，難點(diǎn)在于要從問(wèn)題的條件中推導(dǎo)出用于節(jié)省搜索的性質(zhì)。而策略設(shè)計(jì)問(wèn)題則完全是另一個(gè)世界，因?yàn)椴呗缘脑O(shè)計(jì)空間貌似是可列無(wú)窮的，常常讓人感覺(jué)無(wú)從下手，摸不著頭緒，許多讓人撓頭的智力問(wèn)題就有這個(gè)特點(diǎn)（例如著名的100個(gè)囚徒和1個(gè)燈泡的房間就讓很多人有這種感覺(jué)），策略設(shè)計(jì)問(wèn)題也有一些較通用的法則，以后再說(shuō)。

怎么才能在學(xué)算法的時(shí)候?qū)W到背后的東西呢？有以下幾點(diǎn)很重要：

不要覺(jué)得每個(gè)步驟都很顯然，每個(gè)nontrivial的算法背后都有一段艱辛的探索經(jīng)歷，覺(jué)得顯然的話必然是一種幻覺(jué)。Stay foolish，才能發(fā)現(xiàn)某些環(huán)節(jié)其實(shí)并不是那么顯然的。

檢驗(yàn)是否真正理解的最佳方法就是過(guò)一段時(shí)間之后，自己試著證明一次。如果真正理解了的話，你的證明便會(huì)比較順暢。如果當(dāng)時(shí)沒(méi)有真正理解，那么凡是那些你當(dāng)時(shí)覺(jué)得顯然但其實(shí)不顯然的地方，都會(huì)成為你證明里面缺失的環(huán)節(jié)。

對(duì)于一個(gè)算法，多尋找各種來(lái)源的資料，也許能夠找到一個(gè)講的比較深刻的。我在《數(shù)學(xué)之美番外篇：快排為什么那么快》和《知其所以然（一）》里面都舉到了這樣的例子。

多試著去抽象背后的一般性法則，即便后來(lái)發(fā)現(xiàn)抽象得是錯(cuò)的，也比不去抽象要好。抽象是推廣的基礎(chǔ)。只有抽象出更深層的法則，才能讓你事半功倍，觸類旁通，否則一個(gè)蘿卜永遠(yuǎn)是一個(gè)坑。（注意，其實(shí)我們的下意識(shí)是會(huì)進(jìn)行一定程度的抽象的，例如前面提到的原始人的例子，小溪和小河（或者小溝）細(xì)節(jié)上是不同的，但本質(zhì)上是一樣的，我們的大腦會(huì)自動(dòng)進(jìn)行這種簡(jiǎn)單抽象，提出事物的共性。正因此，即便你不去有意識(shí)地總結(jié)一般規(guī)律，只要你看的足夠多，練的足夠多，必然就會(huì)越來(lái)越諳熟。）

最后留個(gè)問(wèn)題：雖然按照上文的方式來(lái)構(gòu)造霍夫曼樹(shù)一定能夠得到一個(gè)最優(yōu)樹(shù)，但是怎么證明一定能得到呢？乍一看這個(gè)問(wèn)題似乎很多余，因?yàn)樽C明很簡(jiǎn)單：我們拼裝整棵樹(shù)的每一步都沒(méi)得選，而且每一步都必然拼湊出最優(yōu)樹(shù)的一個(gè)小小局部，如果最終還沒(méi)有得到最優(yōu)樹(shù)的話，只能說(shuō)最優(yōu)樹(shù)是不存在的了，然而最優(yōu)樹(shù)是一定存在的，因?yàn)樗袠?shù)的集合是有窮的，有窮集必有最值，因此證畢。這個(gè)證明固然是沒(méi)問(wèn)題的，但它其實(shí)是一個(gè)間接證明，換句話說(shuō)，我們?cè)跇?gòu)建樹(shù)的過(guò)程中的邏輯是這樣的：“之所以我們選擇粘結(jié)n1和n2，是因?yàn)槠渌撤ū厝贿`反最優(yōu)樹(shù)的兩個(gè)性質(zhì)。所以我們別無(wú)選擇。”但是，這并沒(méi)有說(shuō)，我們選擇了粘結(jié)n1和n2，一定就符合了最優(yōu)樹(shù)的性質(zhì)。（也就是說(shuō)“其他做法都是錯(cuò)”并不能推出“這種做法必然對(duì)”，這就像是你在一大堆豆子當(dāng)中尋找一個(gè)特殊的豆子，你拿起一個(gè)，看看不是，扔掉，又拿起一個(gè)，還不是，扔掉，排除到最后只剩一個(gè)豆子了，假設(shè)你又知道這個(gè)特殊的豆子必然存在，那么這個(gè)時(shí)候你根本不用看就知道這個(gè)豆子一定就是你要找的）那么，你能否直接證明，拼裝最優(yōu)樹(shù)的過(guò)程每一步都符合最優(yōu)樹(shù)的性質(zhì)呢？

編輯：黃飛