今天的算法是插值，細(xì)分是牛頓插值。關(guān)于插值可能大家聽到最多的就是圖像插值，比如100元的攝像頭有4K的分辨率？？？其實(shí)這里就是使用的插值算法，通過(guò)已經(jīng)有的數(shù)據(jù)再生成一些，相當(dāng)于提升了數(shù)據(jù)的量。如果我們想放大圖像，我們需要使用過(guò)采樣算法來(lái)擴(kuò)展矩陣。

左邊是原有的信息，右邊是通過(guò)算法生成的新數(shù)據(jù)

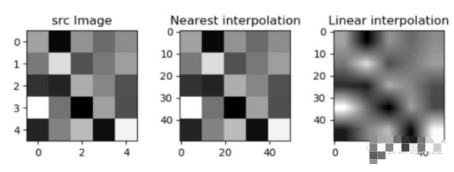
就像這樣

在上圖中，出現(xiàn)的算法是最近鄰算法，也稱為近端插值，是一維或多維空中多元插值的一種簡(jiǎn)單方法。插值是通過(guò)已知的離散數(shù)據(jù)點(diǎn)在一定范圍內(nèi)尋找新數(shù)據(jù)點(diǎn)的過(guò)程或方法。最近鄰插值算法選擇最接近數(shù)據(jù)點(diǎn)的值，完全不考慮其他相鄰點(diǎn)的值，從而生成一個(gè)分段常數(shù)插值值作為數(shù)據(jù)點(diǎn)的值。線性的插值算法是雙線插值是二維坐標(biāo)系下線性插值的擴(kuò)展，用于插值二元函數(shù)。它的核心思想是在兩個(gè)方向上執(zhí)行一次線性插值。

關(guān)于這里的圖像算法我不想說(shuō)什么，等之后我會(huì)補(bǔ)上。簡(jiǎn)單來(lái)說(shuō)在數(shù)據(jù)給的少的情況下我們都可以考慮使用插值算法來(lái)生成新數(shù)據(jù)或者是改善。

注意我們處理的是離散數(shù)據(jù)：離散數(shù)據(jù)是指其數(shù)值只能用自然數(shù)或整數(shù)單位計(jì)算的數(shù)據(jù)。

離散函數(shù)：定義域是離散集合的函數(shù)稱為離散函數(shù)。其函數(shù)圖像為一系列離散的點(diǎn)。

在離散數(shù)據(jù)的基礎(chǔ)上補(bǔ)插連續(xù)函數(shù)，使得這條連續(xù)曲線通過(guò)全部給定的離散數(shù)據(jù)點(diǎn)。插值是離散函數(shù)逼近的重要方法，利用它可通過(guò)函數(shù)在有限個(gè)點(diǎn)處的取值狀況，估算出函數(shù)在其他點(diǎn)處的近似值。

理論就這么多了（其實(shí)也沒(méi)有理論就是說(shuō)下基本的概念）

牛逼的插值算法來(lái)自：

《自然哲學(xué)的數(shù)學(xué)原理》的第三卷的引理五

對(duì)牛頓插值來(lái)說(shuō)，它最大的特點(diǎn)是引入了差商這個(gè)概念。差商即均差，一階差商是一階導(dǎo)數(shù)的近似值。對(duì)等步長(zhǎng)(h)的離散函數(shù)f(x)，其n階差商就是它的n階差分與其步長(zhǎng)的n次冪的比值。例如n=1時(shí)，若差分取向前的或向后的，所得一階差商就是函數(shù)的導(dǎo)數(shù)的一階近似；若差分取中心的，則所得一階差商是導(dǎo)數(shù)的二階近似。

對(duì)一個(gè)f(x)可以構(gòu)造差商表來(lái)遞推的給出差商

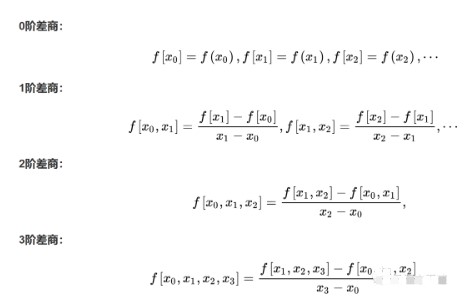
計(jì)算的公式就是這樣，因?yàn)槭侵貜?fù)同一種范式，所以程序?qū)崿F(xiàn)可以使用遞歸

事實(shí)上我們應(yīng)該給出一點(diǎn)更加規(guī)范的論證(不就是個(gè)導(dǎo)數(shù)）

有了上面的定義，作用是給出每一項(xiàng)的系數(shù)。具體推導(dǎo)是這樣的：

最后的就是我們的插值公式

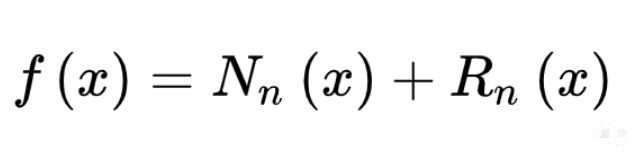
為了看起來(lái)平易近人，可以寫成這樣

還有一種是等間距的插值計(jì)算，在下面的計(jì)算中間距設(shè)置為h（方向?yàn)榍跋虿罘郑?/p>

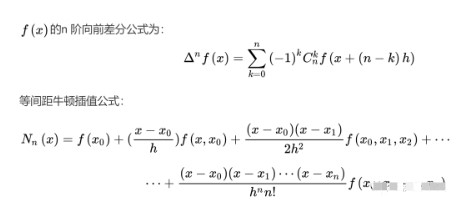
這個(gè)圖就完美了！！！

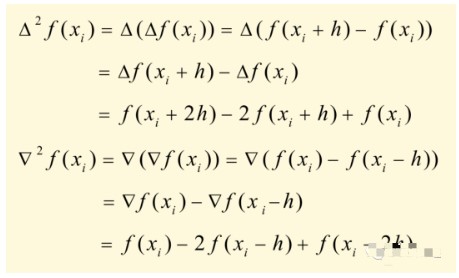
二階的前向差分后和后向差分都在這里了

牛頓插值作為一種常用的數(shù)值擬合方法，因其計(jì)算簡(jiǎn)單，方便進(jìn)行大量插值點(diǎn)的計(jì)算。在實(shí)驗(yàn)中經(jīng)常出現(xiàn)只能測(cè)量得到離散數(shù)據(jù)點(diǎn)的情況，或者只能用數(shù)值解表示某對(duì)應(yīng)關(guān)系之時(shí)，可以使用牛頓插值公式，對(duì)離散點(diǎn)進(jìn)行擬合，得到較為準(zhǔn)確的函數(shù)解析值。

牛頓真厲害啊，幾百年前他萬(wàn)萬(wàn)沒(méi)有想到，一個(gè)小輩大晚上的還得研究人家隨手寫的東西。

牛頓插值算法的優(yōu)點(diǎn)是，每一個(gè)新項(xiàng)的生成都不需要龐大的算力，對(duì)前一項(xiàng)進(jìn)行計(jì)算就行，拉格朗日的算法是每一個(gè)新項(xiàng)都需要對(duì)基函數(shù)完全計(jì)算，耗費(fèi)算力。最后我們的泰勒公式其實(shí)就是對(duì)牛頓的插值算法進(jìn)行了改進(jìn)：

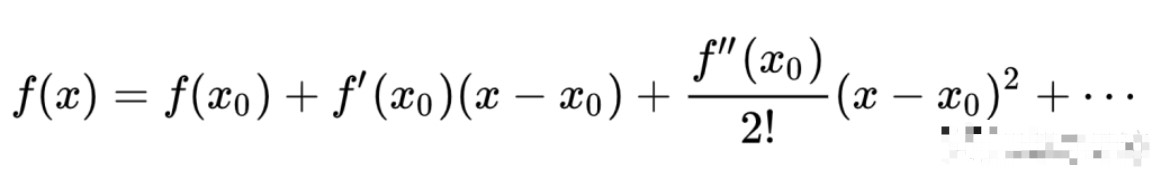
就記幾項(xiàng)就行

對(duì)了，插值是針對(duì)自變量的任何中間值估計(jì)函數(shù)值的技術(shù)，而計(jì)算給定范圍之外的函數(shù)值的過(guò)程稱為外插。

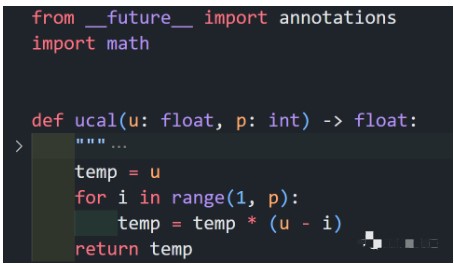
u是啥？別著急

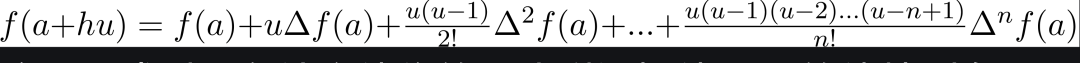
這個(gè)公式對(duì)于在給定值集的開頭附近插值 f(x) 的值特別有用。h 稱為差值區(qū)間，u = ( x – a ) / h，這里 a 是第一項(xiàng)。

函數(shù)就是算這個(gè)的。

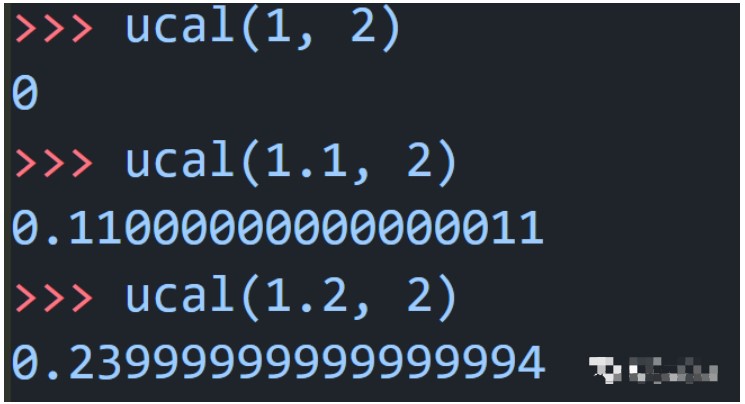
測(cè)試

下面的分母，需要求階乘，這里也準(zhǔn)備一個(gè)小函數(shù)

將輸入的值轉(zhuǎn)為整型，準(zhǔn)備一個(gè)list，將輸入的值輸入到空白的二維數(shù)值表。

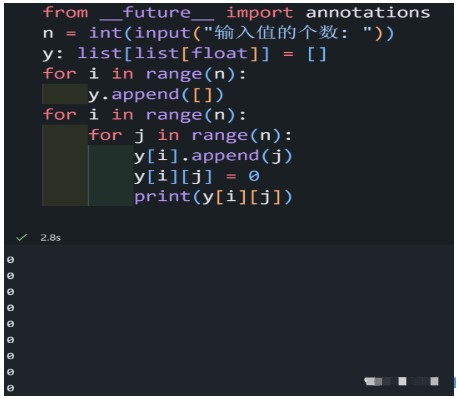
就像這樣

這個(gè)沒(méi)有什么好說(shuō)的，就是將輸入的值解到該有的位置，而且計(jì)算差分值。

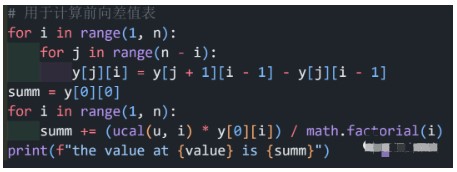
審核編輯：劉清