讀完本文，可以去力扣解決如下題目：

370. 區間加法（中等）

1109. 航班預訂統計（中等）

1094. 拼車（中等）

PS：這是一年前發布的論那些小而美的算法技巧：差分數組/前綴和，我優化并添加了很多內容，重新發一遍。

前文說前綴和主要適用的場景是原始數組不會被修改的情況下，頻繁查詢某個區間的累加和。

這里簡單介紹一下前綴和，核心代碼就是下面這段：

classPrefixSum{
//前綴和數組
privateint[]prefix;

/*輸入一個數組，構造前綴和*/
publicPrefixSum(int[]nums){
prefix=newint[nums.length+1];
//計算nums的累加和
for(inti=1;i1]+nums[i-1];
}
}

/*查詢閉區間[i,j]的累加和*/
publicintquery(inti,intj){
returnprefix[j+1]-prefix[i];
}
}

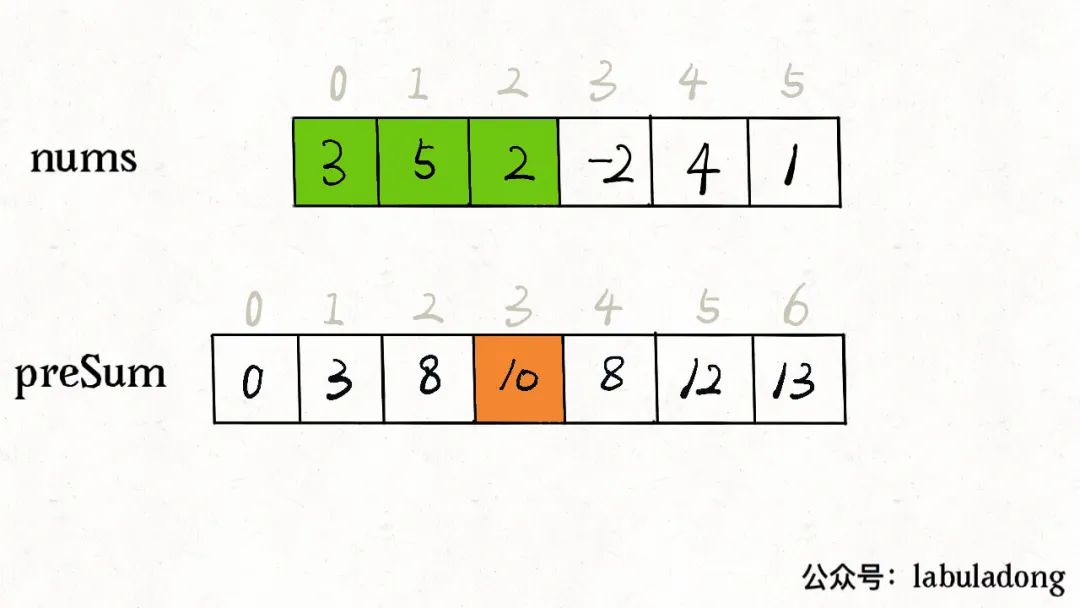
prefix[i]就代表著nums[0..i-1]所有元素的累加和，如果我們想求區間nums[i..j]的累加和，只要計算prefix[j+1] - prefix[i]即可，而不需要遍歷整個區間求和。

本文講一個和前綴和思想非常類似的算法技巧「差分數組」，差分數組的主要適用場景是頻繁對原始數組的某個區間的元素進行增減。

比如說，我給你輸入一個數組nums，然后又要求給區間nums[2..6]全部加 1，再給nums[3..9]全部減 3，再給nums[0..4]全部加 2，再給…

一通操作猛如虎，然后問你，最后nums數組的值是什么？

常規的思路很容易，你讓我給區間nums[i..j]加上val，那我就一個 for 循環給它們都加上唄，還能咋樣？這種思路的時間復雜度是 O(N)，由于這個場景下對nums的修改非常頻繁，所以效率會很低下。

這里就需要差分數組的技巧，類似前綴和技巧構造的prefix數組，我們先對nums數組構造一個diff差分數組，diff[i]就是nums[i]和nums[i-1]之差：

int[]diff=newint[nums.length];
//構造差分數組
diff[0]=nums[0];
for(inti=1;i1];
}

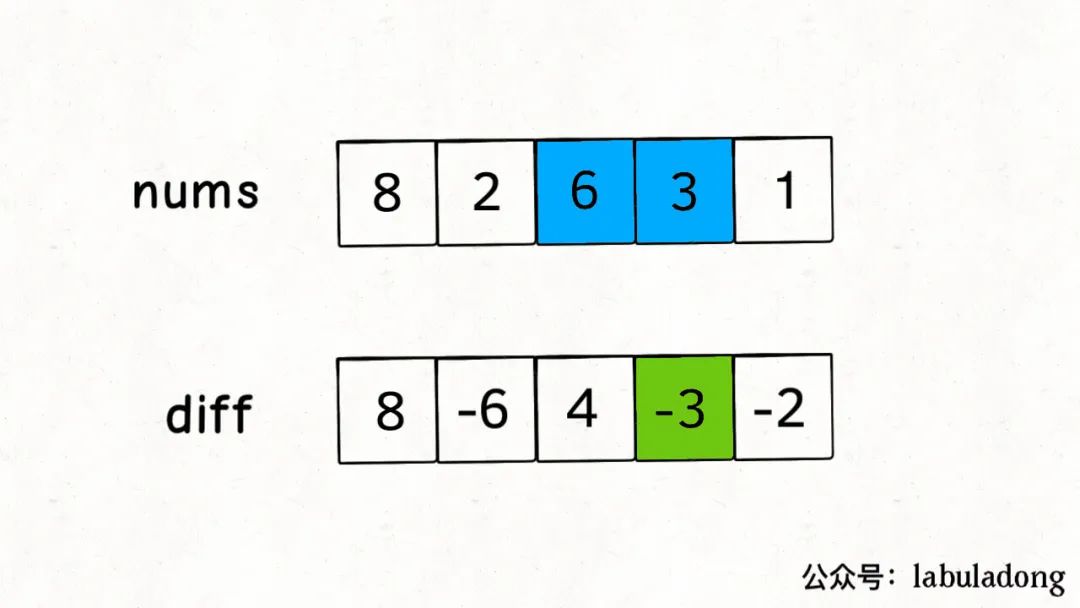
通過這個diff差分數組是可以反推出原始數組nums的，代碼邏輯如下：

int[]res=newint[diff.length];
//根據差分數組構造結果數組
res[0]=diff[0];
for(inti=1;i1]+diff[i];
}

這樣構造差分數組diff，就可以快速進行區間增減的操作，如果你想對區間nums[i..j]的元素全部加 3，那么只需要讓diff[i] += 3，然后再讓diff[j+1] -= 3即可：

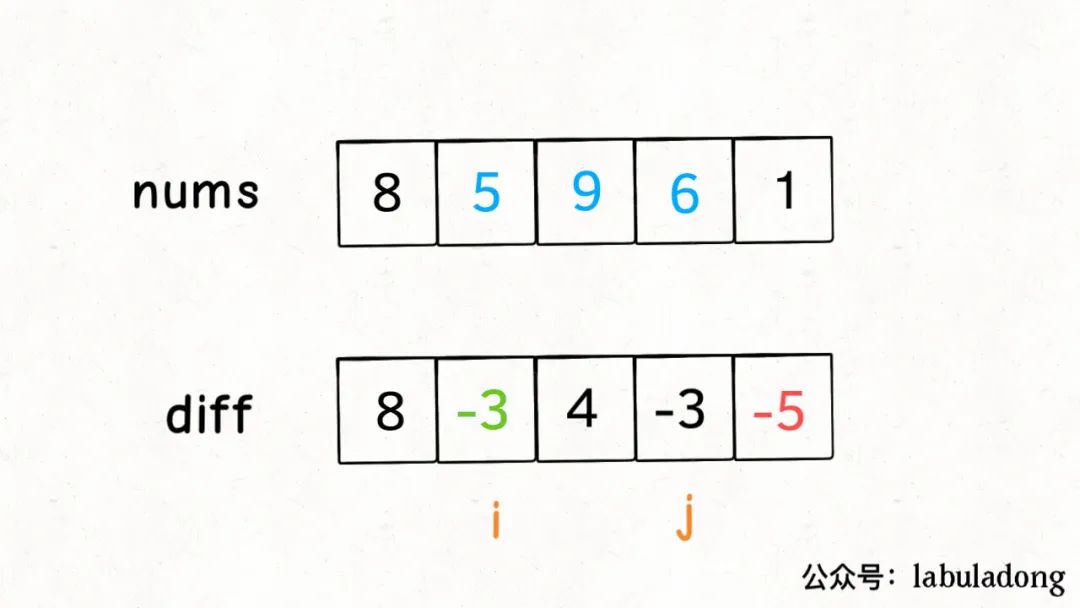
原理很簡單，回想diff數組反推nums數組的過程，diff[i] += 3意味著給nums[i..]所有的元素都加了 3，然后diff[j+1] -= 3又意味著對于nums[j+1..]所有元素再減 3，那綜合起來，是不是就是對nums[i..j]中的所有元素都加 3 了？

只要花費 O(1) 的時間修改diff數組，就相當于給nums的整個區間做了修改。多次修改diff，然后通過diff數組反推，即可得到nums修改后的結果。

現在我們把差分數組抽象成一個類，包含increment方法和result方法：

//差分數組工具類
classDifference{
//差分數組
privateint[]diff;

/*輸入一個初始數組，區間操作將在這個數組上進行*/
publicDifference(int[]nums){
assertnums.length>0;
diff=newint[nums.length];
//根據初始數組構造差分數組
diff[0]=nums[0];
for(inti=1;i1];
}
}

/*給閉區間[i,j]增加val（可以是負數）*/
publicvoidincrement(inti,intj,intval){
diff[i]+=val;
if(j+11]-=val;
}
}

/*返回結果數組*/
publicint[]result(){
int[]res=newint[diff.length];
//根據差分數組構造結果數組
res[0]=diff[0];
for(inti=1;i1]+diff[i];
}
returnres;
}
}

這里注意一下increment方法中的 if 語句：

publicvoidincrement(inti,intj,intval){
diff[i]+=val;
if(j+11]-=val;
}
}

當j+1 >= diff.length時，說明是對nums[i]及以后的整個數組都進行修改，那么就不需要再給diff數組減val了。

算法實踐

首先，力扣第 370 題「區間加法」 就直接考察了差分數組技巧：

那么我們直接復用剛才實現的Difference類就能把這道題解決掉：

int[]getModifiedArray(intlength,int[][]updates){
//nums初始化為全0
int[]nums=newint[length];
//構造差分解法
Differencedf=newDifference(nums);

for(int[]update:updates){
inti=update[0];
intj=update[1];
intval=update[2];
df.increment(i,j,val);
}

returndf.result();
}

當然，實際的算法題可能需要我們對題目進行聯想和抽象，不會這么直接地讓你看出來要用差分數組技巧，這里看一下力扣第 1109 題「航班預訂統計」：

函數簽名如下：

int[]corpFlightBookings(int[][]bookings,intn)

這個題目就在那繞彎彎，其實它就是個差分數組的題，我給你翻譯一下：

給你輸入一個長度為n的數組nums，其中所有元素都是 0。再給你輸入一個bookings，里面是若干三元組(i,j,k)，每個三元組的含義就是要求你給nums數組的閉區間[i-1,j-1]中所有元素都加上k。請你返回最后的nums數組是多少？

PS：因為題目說的n是從 1 開始計數的，而數組索引從 0 開始，所以對于輸入的三元組(i,j,k)，數組區間應該對應[i-1,j-1]。

這么一看，不就是一道標準的差分數組題嘛？我們可以直接復用剛才寫的類：

int[]corpFlightBookings(int[][]bookings,intn){
//nums初始化為全0
int[]nums=newint[n];
//構造差分解法
Differencedf=newDifference(nums);

for(int[]booking:bookings){
//注意轉成數組索引要減一哦
inti=booking[0]-1;
intj=booking[1]-1;
intval=booking[2];
//對區間nums[i..j]增加val
df.increment(i,j,val);
}
//返回最終的結果數組
returndf.result();
}

這道題就解決了。

還有一道很類似的題目是力扣第 1094 題「拼車」，我簡單描述下題目：

你是一個開公交車的司機，公交車的最大載客量為capacity，沿途要經過若干車站，給你一份乘客行程表int[][] trips，其中trips[i] = [num, start, end]代表著有num個旅客要從站點start上車，到站點end下車，請你計算是否能夠一次把所有旅客運送完畢（不能超過最大載客量capacity）。

函數簽名如下：

booleancarPooling(int[][]trips,intcapacity);

比如輸入：

trips=[[2,1,5],[3,3,7]],capacity=4

這就不能一次運完，因為trips[1]最多只能上 2 人，否則車就會超載。

相信你已經能夠聯想到差分數組技巧了：trips[i]代表著一組區間操作，旅客的上車和下車就相當于數組的區間加減；只要結果數組中的元素都小于capacity，就說明可以不超載運輸所有旅客。

但問題是，差分數組的長度（車站的個數）應該是多少呢？題目沒有直接給，但給出了數據取值范圍：

0<=?trips[i][1]?

booleancarPooling(int[][]trips,intcapacity){
//最多有1000個車站
int[]nums=newint[1001];
//構造差分解法
Differencedf=newDifference(nums);

for(int[]trip:trips){
//乘客數量
intval=trip[0];
//第trip[1]站乘客上車
inti=trip[1];
//第trip[2]站乘客已經下車，
//即乘客在車上的區間是[trip[1],trip[2]-1]
intj=trip[2]-1;
//進行區間操作
df.increment(i,j,val);
}

int[]res=df.result();

//客車自始至終都不應該超載
for(inti=0;iif(capacityreturnfalse;
}
}
returntrue;
}