摘要神經網絡量子態是由人工神經網絡所表示的量子態。得益于機器學習,尤其是深度學習近年來取得的突破性進展,神經網絡量子態的研究得到了廣泛的關注,成為當前的熱點前沿方向。文章將介紹不同的神經網絡量子態,其物理性質與典型應用場景,最新進展,以及面臨的挑戰。
01 引 言
人工智能主要有三條發展路線:符號主義、連接主義與行為主義[1]。人工神經網絡是連接主義的基石,也是最近幾年深度學習取得突破進展的關鍵要素之一。它是受到生物大腦中信息處理模式的啟發而提出的,最早可追溯到1943年由心理學家W. S. McCulloch與數理邏輯學家W. Pitts提出的神經元模型[2]。當前,基于神經網絡的人工智能技術正在給人類文明的方方面面帶來革命性的改變[3]:從語音、圖像識別到引力波、黑洞探測,再到數據挖掘、自動駕駛、醫學診斷、證券市場分析,等等。2018 年,計算機科學的最高獎——圖靈獎也被授予三位人工智能科學家Yoshua Bengio,Geoffrey Hinton與Yann LeCun,以表彰他們在相關領域所做的突出貢獻[4]。
另一方面,量子力學是現代物理最重要的基礎理論之一[5]。其重要性廣泛體現在我們的日常生活和科學探索中:從以電子計算機為代表的半導體工業到新奇的超導現象,從隨處可見的化學電池到宇宙中神秘的黑洞,世間萬物的變化規律都與量子力學密切相關。
然而,對量子系統尤其是量子多體系統的研究是非常困難的。實際研究中能夠嚴格解析解決的問題很少,對于絕大部分問題的求解,我們只能依賴于數值方法。對于最一般的情形,數值方法需要消耗指數量級的計算資源,這對于規模較小的物理系統是可行的,但如果系統規模變大,這一指數級的要求在經典計算體系下就難以滿足了[6]。1998年諾貝爾化學獎得主Walter Kohn將這一問題描述為“指數墻(exponential wall)” 困難[7]。為此,物理學家做了大量的努力,發展了一系列計算方法,著名的蒙特卡羅算法以及重正化群算法就是典型代表。但是這些方法并不是通用的,分別有著各自的適用條件。比如蒙特卡羅算法在應用于一些有阻挫系統時會出現符號問題,從而使得算法需要指數級的時間;而密度矩陣重正化群算法一般僅適用于一維低糾纏熵系統。
在人工智能領域中,一個類似的問題是維度災難(curse of dimensionality)。維度災難最早是由動態規劃先驅、著名應用數學家 Richard E. Bellman提出,描述了高維與低維數據集截然不同的性質對計算問題帶來的影響[8]:隨著數據維度增加,有限規模的數據在空間中的分布會逐漸稀疏,從而失去統計意義。這就要求在一般情況下,我們需要非常大的數據規模來獲得數據集的統計特征,但是這會對計算資源帶來嚴重負擔。經過多年的發展,人工智能領域提出了許多用于處理高維問題的方法和工具。人工神經網絡就是一個應用非常廣泛的例子,可以在一定程度上緩解維度災難帶來的困難。簡單來說,人工神經網絡可以看成是一個普適的函數擬合器。通過調節網絡參數,它可以用來擬合任何光滑函數[9]。
由于指數墻困難和維度災難的相似性,一個自然的想法是可以用神經網絡處理復雜的量子問題。如可以用神經網絡識別不同的量子物態以及研究它們之間的相變 (參見《物理》2017年第9期蔡子的專題文章)。另一方面,我們也可以用神經網絡來表示量子態,其主要思想是把神經網絡當成變分波函數,通過調節網絡參數來逼近目標波函數(如多體系統的基態),進而求解所關心的物理問題。傳統的量子多體變分波函數方法需要物理學家針對所求解的問題設計特定的變分函數,而神經網絡量子態方法可以使用相對普適的結構,對于先驗知識的依賴程度較低。此外,人工智能領域里發展的一些優化神經網絡的方法也可以用于神經網絡量子態,提高算法效率。
近年來,通過神經網絡量子態的方法求解量子多體問題受到了廣泛關注[10—12]。當前,這是一個非常活躍的前沿研究方向。本文將介紹不同神經網絡量子態的物理性質與典型應用場景,以及此方向的最新進展。所涉及的神經網絡包括受限玻爾茲曼機,深度玻爾茲曼機,前饋神經網絡,與循環神經網絡等。典型應用包括:求解量子多體系統的基態及動力學演化,探測量子非定域性,量子層析,以及計算交錯時序關聯函數等。希望通過本文的討論,讀者能感受到神經網絡量子態的魅力。眾所周知,基于神經網絡的智能程序 AlphaGo[13]與 AlphaFold[14]分別在圍棋與預測蛋白質結構方面取得了里程碑式的突破。我們期望神經網絡量子態能把這些突破延續到解決復雜的量子多體問題中來。
02 量子態的神經網絡表示
在量子力學中,一個封閉的、不與外界產生關聯的物理系統的全部可能狀態組成一個希爾伯特空間,每個特定的物理狀態由該空間中的一個矢量描述。希爾伯特空間在數學上是線性空間,因此在確定其基矢之后,每一個物理狀態對應的矢量可以表示為選定基矢量的線性疊加。在實際物理問題中,我們經常需要處理包含多個子系統的情況,系統的希爾伯特空間維數為各子系統對應空間維數的乘積[15]。比如,假設我們需要描述包含N個自旋粒子的量子系統,每一個粒子自旋可以取上下兩種可能,其對應希爾伯特空間維數為 2,那么整個系統的自旋狀態就有 2N 種可能,從而總希爾伯特空間維數為 2N。因此,表示最一般情況下的波函數需要指數量級的計算資源。這給數值求解量子多體問題帶來了極大挑戰。
幸運的是,人們關心的物理狀態一般還受到某些限制,比如對稱性的限制或者是某些物理觀測量的限制,每一個子系統并不是完全獨立的,子系統狀態會互相影響,從而整體系統可能的狀態只占據了希爾伯特空間中的很小一部分。原則上可以針對不同的物理系統,利用具有特定結構的表示方法,在使用相對較少的計算資源情況下表示這些物理狀態[5]。著名的張量網絡就是一個典型的例子[16]。物理中一般使用糾纏熵(entanglement entropy)來刻畫量子系統之間的關聯強度。張量網絡可以有效表示糾纏熵滿足面積定律(即糾纏熵與子系統的表面積成正比)的物理狀態[17]。在這里,“有效”指的是只需要多項式量級的計算資源。另一個例子就是本文將要重點介紹的神經網絡量子態。
圖1 神經網絡量子態示意圖 (a) 生物大腦中的神經元;(b)感知機;(c)生物神經網絡;(d) 人工神經網絡;(e) 量子態的神經網絡表示
神經網絡由大量的節點(神經元)及它們之間的相互連接構成,如圖1所示。每個節點包含一種特定的輸出函數,稱為激活函數。每兩個節點間的連接代表對于通過該連接信號的加權值,稱為權重。神經網絡就是通過這種方式來簡單模擬人類的大腦。網絡的輸出則取決于網絡的結構、連接方式、權重和激活函數。神經網絡中的神經元通常被排列成層狀結構,第一層被稱為輸入層,數據由這一層輸入。最后一層被稱為輸出層,中間層被稱為隱藏層。如果一個神經網絡有多于兩層的結構,我們通常稱其為深度神經網絡,基于此構建的機器學習模型稱為深度學習。依據具體網絡結構和信息傳播方向的不同,神經網絡又可以分為很多種。常見的神經網絡有前饋神經網絡、卷積神經網絡、玻爾茲曼機、循環神經網絡等。本質上,量子波函數是一個函數,而神經網絡是一個普適的函數擬合器。因此,我們可以用神經網絡表示量子態。
2.1受限玻爾茲曼機
受限爾茲曼機(restricted Boltzmann machine,RBM)是一類應用非常廣泛的神經網絡,其在數據降維、特征學習、圖片生成、自然語言處理等場景中都有重要應用[18]。它是一個兩層的神經網絡,其中一層稱為可視層,另一層稱為隱藏層。可視層中的神經元可以連接到隱藏層,而同層神經元之間不能相連。
考慮一個由N個量子比特組成的系統,其量子態的一般形式為
, 其中σ= (σ1,σ2,?,σN) 表示一個可能的構型。ψ(σ) 可以看成是一個函數,輸入為σ,輸出為一個復數ψ(σ),表示分量對應的振幅和相位信息。如圖2所示,可以用一個可視層有N個神經元(對應N個量子比特),隱藏層有M個神經元的RBM來表示 ψ(σ) [19]
其中
表示隱藏神經元的可能構型,每個神經元有兩個可能的取值 σi = ±1 和 hj = ±1,ai,bj與 wij 分別表示網絡的偏置和連接參數。為簡單起見,我們稱由受限玻爾茲曼機所表示的量子態為RBM態。
圖2 量子態的受限玻爾茲曼機表示
數學上可以證明,當M取值足夠大時,受限玻爾茲曼機可以以任意精度逼近任何光滑函數。因此,原則上量子態的受限玻爾茲曼機表示是完備的,任何量子態都可以用受限玻爾茲曼機表示。實際應用中,M一般隨N多項式增大,所以RBM表示量子態所需要的參數個數也是隨N多項式增加,而不是指數增加。如此,RBM態在解決某些量子多體問題的時候就可能可以繞過“指數墻”困難。
與張量網絡表示不同,受限玻爾茲曼機可以有效表示具有大糾纏熵的量子態[20]。這得益于可視神經元與隱藏神經元的長程連接。事實上,我們可以解析構造一個滿足糾纏熵體積定律(即糾纏熵與子系統體積成正比)的RBM態,其所包含的參數個數隨N僅為線性增加。而如果用常規的張量網絡表示同樣的量子態,所需的參數個數隨N是指數增加的。這體現了神經網絡在表示大糾纏熵的量子態方面的獨特優勢。
如果我們限制只有近鄰的可視神經元能連接到同一個隱藏神經元,這樣可以進一步降低參數規模及優化難度,所得到的量子態稱為短程RBM態。由于這個限制,任意可視神經元只關聯到其附近的神經元。因此,所有短程RBM態都滿足糾纏熵面積定律。
圖3 受限玻爾茲曼機表示拓撲態 (a)環曲面碼哈密頓量;(b)基態的RBM表示;(c)含4個準粒子的激發態
短程RBM可以嚴格表示一些有趣的奇異量子態,如拓撲態、超圖態等。拓撲態的一個重要例子是環曲面碼態(toric-code state)[21],它是 Alexei Kitaev 提出的環曲面碼哈密頓量(圖3(a))的基態,在拓撲量子計算[22]與量子糾錯中極為重要。圖3(b)簡要描述了環曲面碼態的短程RBM表示。在環曲面碼態的基礎上,作用弦算符(即由不同格點泡利矩陣張量積所得算符)可以得到系統的激發態。如圖3(c)所示,此激發態含有4個準粒子,分別位于弦算符 P1x 與 P1z兩端。有意思的是,這些激發態都可以用短程RBM 嚴格表示,且所需要的參數個數只隨系統規模線性增加[23]。基于此,我們有一個直接推論,由短程 RBM 表示的環曲面碼態及其激發態都滿足糾纏熵面積定律。而傳統方法證明此結論需要涉及比較復雜的數學工具(如商群)。
以上,我們討論了量子系統純態的 RBM 表示。實際中的量子系統不可避免地受到環境的干擾,其狀態是一個混合態,需要用密度矩陣算符來描述。受限玻爾茲曼機也可以用來表示混合態[24]。需要指出的是,為滿足密度矩陣半正定性的要求,表示混合態時受限玻爾茲曼機的參數需要滿足特定的條件。此外,通過附加行列式或使用 Grassmann 代數的方法,受限玻爾茲曼機也可以用來表示費米子系統的量子態[25,26]。
2.2 深度玻爾茲曼機
受限玻爾茲曼機可以有效表示一些有趣的量子態,但其表示能力有限。例如,它不能有效表示一些可以展示量子優勢(quantum supremacy)的態,如二維團簇態通過特殊幺正變化所得的態[27]。這個結論可以從直觀上理解,由于受限玻爾茲曼機簡單的結構,其所表示的量子態可以通過有效算法求得。假設其能有效表示可以展示量子優勢的態,這就意味著經典計算機可以有效模擬這個量子態,這與此量子態可以展示量子優勢是矛盾的。
為加強受限玻爾茲曼機的表達能力,可以在原有網絡上再加一層隱藏層,所得網絡稱為深度玻爾茲曼機(deep Boltzmann machine,DBM)。在計算復雜度理論中,一個被普遍接受但至今無法證明的猜想是復雜度的多項式層級不會塌縮,著名的 P ≠NP 猜想是這個猜想的一個特例。在假設以上猜想成立的情況下,可以證明:DBM相比RBM在表達能力上可以有指數級的優勢。存在一些量子態,如果用RBM表示需要指數級的參數, 而DBM只需要多項式規模的參數[28]。
2.3 前饋神經網絡
前饋神經網絡是研究最早和最簡單的神經網絡之一,也是目前應用最廣泛,發展最迅速的人工神經網絡之一[18]。其神經元分層排列,每個神經元只與前一層神經元相連。信息從輸入層逐層傳遞到輸出層,單向傳播無反饋。與受限玻爾茲曼機一樣,前饋神經網絡也可以用來表示量子態[29]。其輸入層所含神經元數目對應所考慮量子系統的粒子數,輸出層為單個神經元,輸出一個復數,表示量子態對應分量的振幅和相位信息。
對于非常復雜的量子態,我們可以將波函數分作兩個部分:波函數絕對值與對應的符號,并分別使用兩個前饋神經網絡表示。在實際應用中可以觀察到,對于簡單的量子態,前饋神經網絡可以準確學習到其對應的符號規則;對于一些復雜的量子態前饋神經網絡也能學習到比較高的精度,這證實了利用前饋神經網絡處理量子態的有效性[29]。
2.4 其他神經網絡
人工智能領域針對不同的問題設計了多種多樣的神經網絡,原則上所有類型的神經網絡都可以用于表示量子態。不同的網絡有不同的結構,能有效表示的量子態以及網絡訓練的時間復雜度也不盡相同。在實際應用中,我們可以根據具體問題選擇不同的神經網絡[18]。比如循環神經網絡(recurrent neural network,RNN)非常適合處理序列數據,在機器翻譯、語音識別以及文本生成等領域有著廣泛的應用。可以將多體系統中量子比特構型視為序列數據,從而利用循環神經網絡來表示量子多體態[30]。卷積神經網絡(convolutional neural network,CNN)則是另一類被廣泛使用的深度神經網絡,適合圖像處理、行為認知、遷移學習等場景。文獻[31]表明,卷積神經網絡也可以用來表示量子態,如前面提到的環曲面碼態。
03 神經網絡量子態的應用 制備方法
如前所述,人工神經網絡可以非常有效地表示多體量子態,其在量子物理,尤其是解量子多體問題中有很廣泛的應用。圖4歸納了當前神經網絡量子態的主要應用。接下來,我們簡要介紹部分近期的相關工作,主要側重于RBM量子態的應用。
圖4 神經網絡量子態的應用
3.1 求解量子系統基態和動力學演化
一個孤立封閉的量子系統可以由哈密頓量描述,其演化過程滿足薛定諤方程。求解給定哈密頓量的基態和動力學演化是量子物理中常見的基本問題。對于少數特殊的模型,如一維伊辛模型(Ising model),其基態和動力學可以通過解析的方法嚴格求解。然而,實際研究中能夠解析求解基態和動力學的情況很少,我們需要依賴數值方法。
利用神經網絡求解基態和動力學的核心想法是把神經網絡量子態看成變分函數,通過梯度下降算法優化網絡參數求解相應問題。以受限玻爾茲曼機為例,G. Carleo 和 M. Troyer 首先求解了幾個典型的量子磁性模型(如伊辛模型、海森伯模型)的基態及動力學,并與傳統的密度矩陣重正化群等方法進行了比較[19]。結果表明,神經網絡的方法使用較少的參數就得到了相近精度的基態能量和動力學演化,這在一定程度上展示了神經網絡方法的優越性。
值得指出的是,對于最一般情形求解基態和動力學演化可以證明是NP問題。因此,神經網絡的方法也不能有效求解所有量子系統的基態和演化。當前的研究表明,其在解決涉及大量子糾纏與高維系統的問題中相比傳統方法可能有優勢,但是這一優勢還沒有得到確切的證明。如何判斷給定哈密頓量的基態和動力學是否可以通過神經網絡的方法有效求解是此領域里一個亟待解決的重要問題。這一問題的解決可能需要發展新的物理概念和數學工具。
3.2 交錯時序關聯函數
交錯時序關聯函數(out-of-time ordered correlator,OTOC)最早由A. Larkin與 Y. Ovchinnikov在1969年研究超導理論時提出[32]。經過幾十年的發展,OTOC在表征量子混沌,量子信息置亂(information scrambling),動力學相變等研究中都有重要應用。此外,其還可以給通過Ads/CFT對偶研究量子引力與黑洞帶來新的啟示。最近,實驗測量OTOC也在離子阱、固態自旋、玻色—愛因斯坦凝聚等系統中實現。
考慮量子多體系統中在空間上分開的兩個局域算符 W 與 V ,其對應的OTOC定義為
其中
為W在海森伯繪景中的時間演化算符。不難看出,OTOC的物理意義是描述一個局域擾動傳播一段時間后,在另一個地方被探測到的物理現象。數值上,計算多體系統的OTOC是非常困難的,其復雜程度要大于基態或動力學演化的求解。文獻[33]提出了 OTOC 的神經網絡求解辦法,其核心思想是把OTOC看成是兩個隨時間演化量子態的交疊,從而通過計算態的演化與交疊來求解。
3.3 量子非定域性
非定域性是量子系統一個非常奇特的性質,是量子物理與經典物理最核心的區別之一[34]。它描述比量子糾纏更強的關聯——任何表現非定域性的量子態一定是糾纏的,反之則不一定成立。在實際應用中,量子非定域性是構建設備無關量子技術,如無條件安全量子密鑰分配、自認證隨機數產生器等,不可或缺的資源。對量子非定域性的思考和研究最早可以追溯到20世紀初發生在愛因斯坦和玻爾之間關于“上帝是否會擲骰子”著名爭論[35]。1964年,約翰·斯圖爾特·貝爾(John Stewart Bell,圖5)提出了著名的貝爾不等式[36]。從此,量子非定域性可以通過實驗測試貝爾不等式的破壞來定量刻畫。
圖5 約翰·斯圖爾特·貝爾(John Stewart Bell,1928.6.28—1990.10.1)。圖片來源于網絡
然而,由于存在指數墻困難,在量子多體系統中研究非定域性變得極為不易。在文獻[37] 中,本文作者之一把機器學習的方法引入到了量子多體非定域性的研究中。其核心思想是把在量子多體系統中探測非定域性的問題轉化為求解哈密頓量基態能量問題,從而可以利用上述神經網絡量子態的方法處理。具體來說,對于給定的量子多體系統,其所有可能的經典關聯組成一個高維空間的多面體,多面體的每一個面對應一個貝爾不等式,如圖6所示。初始時,我們隨機產生一個RBM量子態,其對于給定的觀測量一般只表現出經典關聯。通過不斷地優化RBM的參數,其所表示的量子態逐漸超越多面體的一個面(即破壞對應的貝爾不等式),展示出量子非定域性。值得指出的是,神經網絡量子態在探測多體非定域性問題中有獨特優勢,可以解決一些用傳統方法無法解決或極為困難的問題,比如計算隨機全關聯系統貝爾不等式最大破壞值。
圖6 神經網絡探測貝爾非定域性
3.4求解開放系統穩態和動力學
孤立量子系統演化過程遵循薛定諤方程,而實際系統往往不可避免地與環境發生作用,因此很多情況下并不能當作孤立系統處理。對于與環境弱耦合的開放系統,其狀態的演化可以近似認為僅與當前狀態相關,而與之前的演化過程無關,從而通過玻恩—馬爾可夫近似,可以導出開放系統所滿足的演化方程,即Lindblad主方程[38]:
其中L 為劉維爾超算符,H 表示系統哈密頓量,ρ 為密度矩陣,cj 與γj分別表示耗散算符與耗散強度。
與孤立系統類似,神經網絡的方法也可以用來求解開放量子系統的穩態與動力學演化,此時需要使用密度矩陣的神經網絡表示[24]。與孤立系統不同的是,開放量子系統的能量不再是守恒量,因此不能通過對能量的變分來求解。但是,我們可以考慮優化變分近似演化與精確演化之間的距離或者通過 Choi—Jamio?kowski 同構把主方程轉化為有效哈密頓量方程來求解。與之相關地,我們在文獻[39]中進一步把神經網絡的方法推廣到了劉維爾能隙的求解中。
3.5 量子態層析
量子態層析(quantum tomography)是通過對很多份相同量子態的測量來估計一個未知的量子態[15]。它是校準量子系統,檢驗量子操作的重要技術。同樣的,由于希爾伯特空間維度隨系統規模指數增大,多體系統的量子態層析也變得極為困難。以谷歌公司2019年實現量子優勢的實驗為例[40],其量子線路涉及53個量子比特,對如此大規模的量子態層析最直接的方法需要確定 253 ≈1016個參數,即使是存儲這些參數也至少需要 105 TB 的存儲空間,遠大于當前世界上最先進的超級計算機的內存空間。
神經網絡可以有效表示部分量子態,其所需參數個數只隨系統規模多項式增加。因此,通過神經網絡的方法進行量子態層析只需要確定多項式規模的參數,可極大地減少所需資源。事實上,神經網絡量子態層析已經被多篇論文提出[30,41],并得到了較多關注。最近,部分相關的理論方案也在實驗上得到了驗證[42]。
04 展 望
神經網絡量子態是最近幾年蓬勃發展的交叉前沿方向。當前,這個方向的研究已經取得了一些令人興奮的成果。然而,總體來說其發展還處于初級階段,很多重要基本問題亟待解決。首先,神經網絡表達量子態為何有效及其局限性并未被完全理解。給定一個量子態,我們無法有效判斷它是否可以用某個神經網絡有效表達。這與矩陣直積態或更廣的張量網絡態在早期的發展相似。由于量子信息領域的飛速發展,現在我們知道量子糾纏是張量網絡有效表示量子態的關鍵,也是判斷具體問題能否用相關算法有效解決的前提。然而,量子糾纏并不是神經網絡表達量子態的核心要素,理解神經網絡有效性及局限性可能需要發展新的物理概念與數學工具。其次,神經網絡量子態的“殺手級應用”還未發現。當前已有的研究大多數還處在原理演示階段。人們發現了很多問題可以用神經網絡解決,但這些問題大多數也可以用傳統方法處理,神經網絡并不是唯一解決途徑。再次,如何利用神經網絡方法有效解決強阻挫量子磁性系統或強相互作用費米子系統相關問題仍是未解之謎。這些問題是量子多體物理中極為重要,卻最具挑戰性的問題。
總之,神經網絡量子態在機器學習與量子物理之間架設了新的橋梁。這個方向的研究有利于不同學科之間的交叉融通,對機器學習與量子物理的發展都大有裨益。當前,這個方向正在蓬勃發展,挑戰與機遇并存。鑒于AlphaGo與AlphaFold的成功,我們有理由期待未來神經網絡量子態在解決復雜的量子多體問題中取得重要突破,大放異彩。
原文標題:神經網絡量子態及其應用
文章出處:【微信公眾號:中科院長春光機所】歡迎添加關注!文章轉載請注明出處。
責任編輯:haq
-
神經網絡
+關注
關注
42文章
4808瀏覽量
102817 -
人工智能
+關注
關注
1804文章
48726瀏覽量
246620 -
機器學習
+關注
關注
66文章
8492瀏覽量
134117
原文標題:神經網絡量子態及其應用
文章出處:【微信號:cas-ciomp,微信公眾號:中科院長春光機所】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
谷歌Gemini API最新進展
京東方華燦光電氮化鎵器件的最新進展
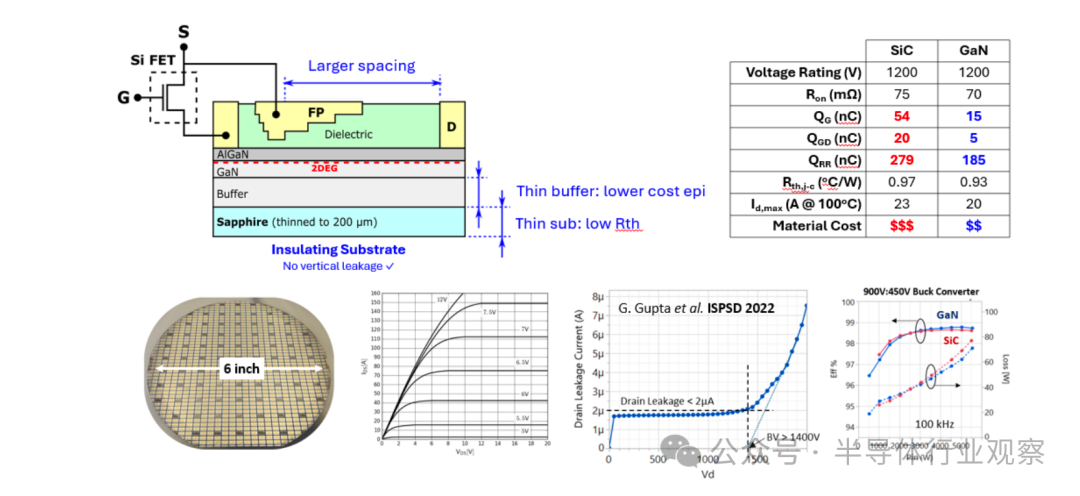
垂直氮化鎵器件的最新進展和可靠性挑戰
FF將發布FX品牌最新進展
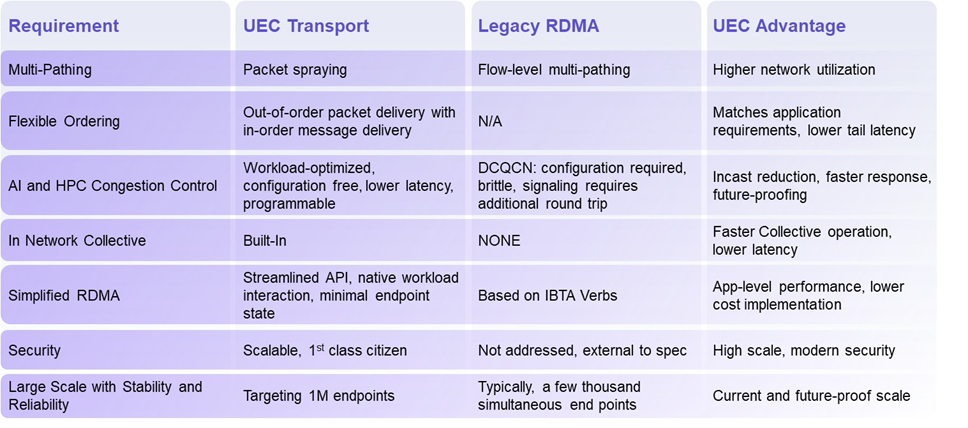
揭秘超以太網聯盟(UEC)1.0 規范最新進展(2024Q4)





 不同神經網絡量子態的最新進展以及面臨的挑戰
不同神經網絡量子態的最新進展以及面臨的挑戰










評論