二階零極點

我們先重新學習二次函數的根的表達式。我們在高中學的二次函數根長這樣：

但是問題是，這樣的表達式是高熵的，比如某一個傳輸函數的分母的根按照傳統高中學過的表達式，長這樣：

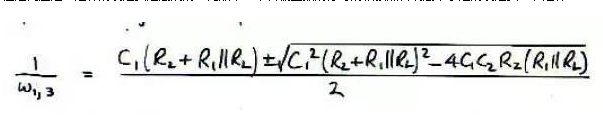
你看這個表達式，長得這么丑，看著就渾身難受。除非你用一個繪圖軟件，并把所有R C的值帶入，否則你沒有辦法快速找出這兩個根的關系，沒法根據這個表達式快速繪出頻率響應。更重要的是，你沒有辦法從這個表達式快速看出要怎樣設計R C以達到你的目的。

所以Prof. Abidi（原引Prof. Middlebrook）教育我們要用適合電路設計的二次函數根式。

回去看高中根式，其實這個根式用的是兩根之和等于-b/a 的性質。但是二次函數兩根之積還等于c/a，新根式正是運用了兩根之積性質。換句話說，高中公式看的是兩根的算術平均，新根式看的是兩個的幾何平均。不要忘了在對數刻度中，幾何平均比算術平均更加有意義，因為兩個刻度的中點是幾何平均。

新根式如下：

注意看新根式的對稱性！拿到一個二階表達式，我們只要算Q和ω0就可以了。有同學會問，那F怎么辦，F不是還是亂糟糟么？其實不然，我們把F和Q的關系畫一下：

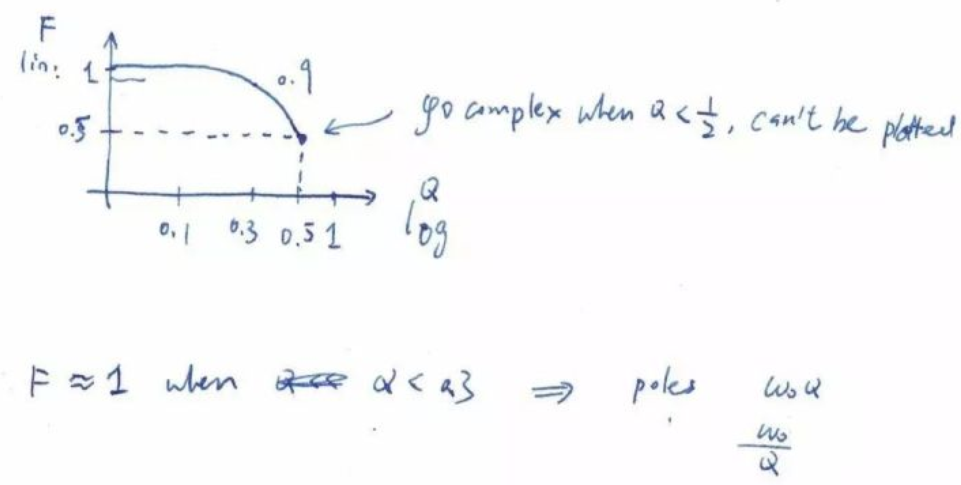
你看，當Q小于0.3的時候，F約等于1。所以我們只要根據Q的表達式，估計Q值，如果遠小于0.3，那么就是兩個實根，一個是-ω0Q，另一個-ω0/Q 啦！

有同學會問，那Q 在0.3和0.5中間時候怎么辦呢？很簡單，把他們近似成兩個重實根就好了。

如果Q大于0.5，我們就有復數根（共振）了。

這樣的表達式利于具體的電路設計。我們可以分析電路模型，把ω0和Q用電路元件的參數表達出來。之后比如我們可以設計 ω0以達到帶寬要求。設計Q 以達到穩定性要求。