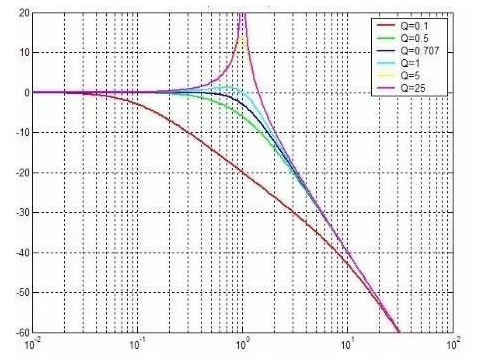
零點和極點對頻率響應的影響可以總結為：

*當頻率遠小于某零點/極點的模時，該零點/極點對頻率響應的影響可以忽略。

*當頻率接近某極點的模時，該極點的效果漸漸體現。當頻率遠大于該極點時，該極點使得頻率響應的幅度以20dB/dec的速度衰減，而相位相對DC產生-π/2的變化。

*共軛極點是一種特殊的極點，它們總是成對出現且共軛極點對的模都相等，因此當頻率遠大于一對共軛極點的模的時候，該共軛極點對會使頻率響應的幅度以40dB/dec的速度衰減，而相位相對DC產生-π的變化。而在頻率接近共軛極點對的模的時候，頻率響應曲線的變化取決于共軛極點對的位置（詳見下文）。

*當頻率接近某零點的模時，該零點的效果漸漸體現。當頻率遠大于該零點時，該零點使得頻率響應的幅度以20dB/dec的速度增加。而相位相對DC產生π/2（當零點在左半平面）或-π/2（當零點在右半平面）的變化。

*頻率響應的總體幅度/相位取決于所有零點和極點對幅度/相位的貢獻。

共軛極點對

共軛極點對是一類特殊的極點。一對共軛極點（s-p）（s-p*）可以寫作

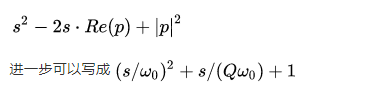其中ω0為共軛極點的諧振頻率，Q稱作共軛極點的品質因數。

共軛極點對模型最初來源于LC諧振電路，如下圖中的RLC串聯電路。

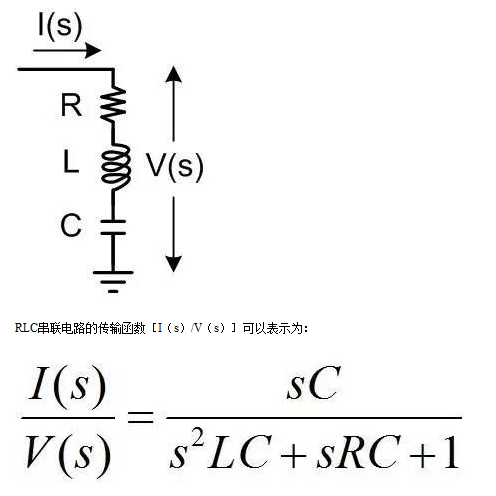
其中共軛極點的諧振頻率ω0=1/√LC即LC tank的諧振頻率，品質因數Q=（1/R）?√（L/C）即為LC tank的品質因數，表示在諧振頻率附近每周期LC tank存儲的能量與耗散能量的比值。共軛極點可以由LC tank形成，也可由反饋通路形成。

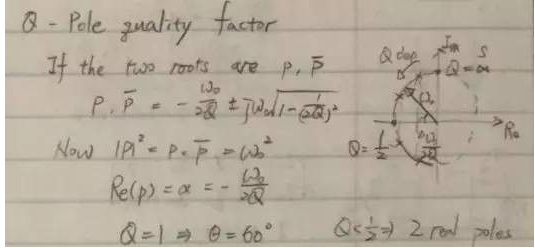
共軛極點對的Q值由共軛極點的位置決定。當共軛極點的諧振頻率固定而改變品質因數（即固定L和C而改變R）時，共軛極點對的軌跡在以原點為圓心，半徑為ω0的圓上。當共軛極點對靠近縱軸時，品質因數變大；而當共軛極點對靠近橫軸時，品質因數變小。共軛極點對的品質因數必須大于等于1/2，當Q小于1/2時共軛極點對退化為兩個實極點。

對于傳輸函數具有共軛極點對的系統，系統的自然響應中含有包絡指數衰減的正弦波。有時候在放大器的瞬時響應中會看到衰減震蕩的現象，這種現象就是由共軛極點造成的。

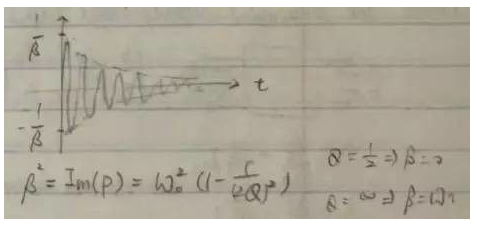
正弦波的頻率接近諧振頻率ω0，而包絡的衰減速度取決于Q。Q值約等于包絡衰減到初始值的1/e時所需要的諧振周期。Q值大時包絡衰減較慢，反之Q值小時包絡衰減較快。在放大器設計中我們往往希望看到settling time比較小的瞬時響應，因此應該避免高Q值得共軛極點對。

共軛極點對另一個重要性質是它會引起頻率響應的尖峰（peaking）。這一點可以從零極點圖來理解。

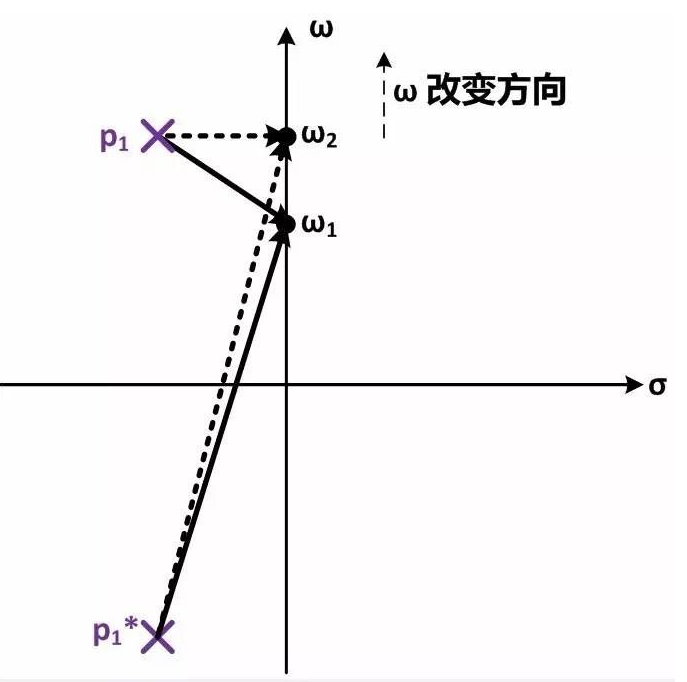
在零極點圖上，有共軛極點p1和p1*，位置在σ±jω0。當頻率從ω1（略小于ω0）移動到ω2（等于ω0）時，連接到極點p1*的極點向量長度基本不變，但連接到極點p1的極點長度顯著變短了。因此頻率響應在諧振頻率（ω=ω0）處會產生一個尖峰，尖峰的高度隨Q值變大而變大。極端情況是Q值無窮大時，此時p1和p1*都在ω軸上，因此當ω=ω0時，連接p1和ω的極點向量長度為0，這樣頻率響應的幅度變為無窮大，所以就產生了高度無窮大的尖峰。在設計需要較小settling time的放大器時我們希望避免明顯的頻率響應尖峰（頻率響應尖峰明顯=》共軛極點對Q值大=》瞬時響應中衰減震蕩持續時間較長=》settling time較長）；但另一方面在設計寬帶放大器（例如在CML電路中）時我們往往會故意引入頻率響應尖峰以增加帶寬。