航跡起始作為空間飛行器跟蹤領域的重要課題，多年來被國內外很多學者研究探討。本文提出的算法根據新測量點在默認關聯波門中的實際情況，采用自適應的可變波門和點關聯判斷準則，實現了在不顯著增加算法復雜度的情況下，同時快速起始直線和曲線航跡的目的。

可變邏輯算法綜述
1 文章符號
zj(i)：第i個雷達掃描周期的第j個測量值。
其中，j∈{1,2,…,m(i)}，m(i)表示傳感器在i時刻收到的測量總數。
v(n)：第n個雷達掃描周期的速度估計。
ts：雷達掃描周期。
z(k)：第k周期的目標位置估計。
α(k)：第k周期的目標加速度估計。

2可變邏輯航跡起始算法
在綜合考慮航跡起始的實際情況前提下，我們得出以下幾個基本假設。

● 空間航跡的運動形態中，目標直線運動的概率Pl遠大于曲線運動的概率Pc。

● 各個空間目標之間是相互獨立的。

由此，本文提出的可變邏輯航跡起始算法流程如下。
①前兩個周期的測量相互配對分別得到各自的速度估計：v(2)=[zk(2)-zj(1)]/ts，滿足vmin‖v(2)‖＜Vmax的測量對成為過渡航跡。對第3周期的目標位置估計為z(3)=zk(2)+v(2)ts。

②以z(3)為中心建立圓形的關聯門1，根據v(2)的大小確定角度約束值σ（σ的值與測量誤差有關）；再根據約束值，重新確定角度關聯門2。在該周期，如果有單個點落入關聯門2內的測量zm(3)，則直接確定該點為新關聯點，如果有多個點落入，則選擇與z(3)距離最近的點作為新關聯點。過渡航跡點數加1，然后根據 v(3)=[zm(3)-zj(2)]/ts，α(3)=[v(3)-v(2)]/ts，得到下一個周期的位置估計z(4)=zm(3)+tsv(3)+1/2ts2α(3)。

③如果在關聯門2中沒有點落入，則檢測關聯門1內有無新點落入。設新點落入個數為Nnew，有：
A Nnew=0，沒有新點落入，則該行跡在該周期沒有關聯點。

B Nnew≥1，有新點落入。以其中一點zm(3)為例，我們認為此點的可靠性較差，需要延遲一步檢測。此時，針對zm(3)的第四周期位置是z(4)=zm(3)+tsv(3)+1/2ts2α(3)。以z(4)為中心， v(3)+α(3)ts為半徑作圓形關聯門。如果有新點落入該關聯門，則選取離z(4)最近的點作為新關聯點，同時認定zm(3)是有效的關聯點。如果沒有新的關聯點落入，認為zm(3)是無關點。

④沒有與任何航跡配對的新點重復步驟①。

3 航跡檢測概率和可變邏輯算法特性
本文算法中，如果航跡是直線型或近似直線型，包括勻速和勻加速直線運動，本文算法實際上就是修正的邏輯航跡起始方法。不同的是在第二個雷達掃描周期，用到了加入修正值的速度門。如果航跡出現轉彎，那么，關聯門1替代關聯門2進行跟蹤，用到了延遲算法。

下面是利用統計學的觀點對延遲算法的航跡檢測概率和假航跡起始概率進行推導。為了不造成混亂，我們只考慮圓關聯門的延遲算法。

首先，我們作如下假設。
①各個空間目標之間是相互獨立的。

②為便于計算，本部分所關注的目標在x方向作勻速直線運動，速度為v，目標在x，y方向上的誤差服從正態分布：N（0，σ2）。

③所用的延遲航跡起始算法前兩點的獲取與前述方法相同，假設第3周期，有一個點zm(3)滿足與預測點z(3)=zk(2)+v(2)ts的距離小于固定門限，判斷第4周期有無新點zm(4)落入以z(4)=zm(3)+tsv(3)+1/2ts2α(3)為中心，半徑為R的圓內，有則認為zm(3)，zm(4)關聯成功，航跡起始成功；否則，認為此條過渡航跡為虛假航跡而從系統刪除。

4 航跡檢測概率（Pd）
由假設可知，目標在第周期的測量為
xi=(i-1)tsv+ξi，yi=ζi??? （1）
其中，ξi，ζi為測量誤差。

傳統的邏輯法采用單步檢測的方法，Pdi為第i個掃描周期的目標檢測概率，在4/4起始邏輯下，Pd=Pd2Pd3Pd4。

基于一步延遲的航跡起始方法是將后兩個掃描周期的點同時考慮，只有兩點同時關聯，才能保證前一個周期點起始成功。設為第i個掃描周期的目標檢測概率（右上標Y表示延時），為航跡檢測概率。
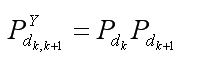????????????? （2）
在m/m邏輯下，對于普通邏輯算法：
Pd=Pd2Pd3Pd4…Pdm????????? （3）
對于一步延遲算法，由于第k周期的點監測成功后，第k+1周期一定有點，

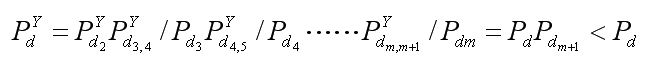?????????????????? （4）
所以，一步延遲算法的航跡檢測概率，在m/m邏輯下是標準算法的航跡起始概率與第m+1步的航跡點檢測概率的乘積。可見，基于一步延遲思想的起始算法的航跡起始概率要低于普通的邏輯法。但是，由于真實航跡的點符合線性相關性（第k周期的點在以k-1和k-2周期點外推的關聯域內），所以大多數情況下，接近1，不會明顯降低航跡的檢測概率。
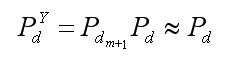??????????? （5）
5 假航跡起始概率（Pf）
假航跡起始的原因是由于空間雜波點的原因，我們通常認為，每個周期的雜波數量服從泊松分布，雜波點位置在觀測域內均勻分布。

Pf為虛假航跡檢測概率，為第i個掃描周期的雜波檢測概率。我們約定，為一步延遲算法下虛假航跡的起始概率，為第k周期雜波點的檢測概率。
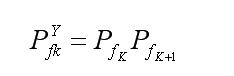????????????? 　（6）

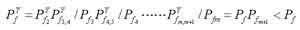????????????????? （7）
第k周期（k>2）的關聯門雜波點的檢測概率為
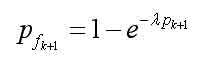????????????? （8）
其中，。
可知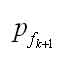，不接近1，可以利用其在一定程度上降低假航跡起始概率。

實驗仿真
1具體環境
（１）監視域范圍：x∈[-4km，4km]，y∈[-4km，4km]的正方形區域。
（2）監視域內虛警數量：在單位周期內，數量服從參數為λ的泊松分布，在整個監視域均勻分布。
（3）采樣間隔T=1s。
（4）航跡模型有如下兩種。
①直線運動（CV和CA）
②勻轉彎角速度運動(CT)。

2 仿真一
本仿真的待起始航跡為4條直線航跡和2條CT航跡。其中，CT航跡的角速度為0.1rad/s和0.2rad/s。
在上述待起始航跡中，每周期加入參數為10的泊松分布噪聲，即期望個數為10/km2。圖2為5/5基本邏輯法的起始結果，圖3為本文的算法起始結果。可見本文算法一定程度上降低了假航跡檢測概率，而真航跡檢測概率未受大的影響。

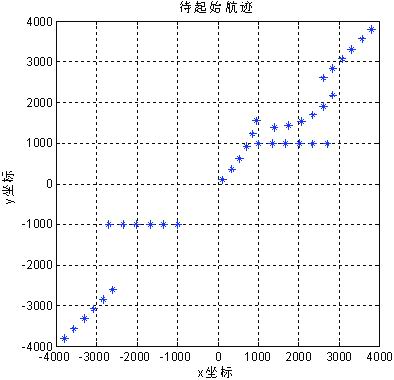
圖1 實驗用待起始航跡

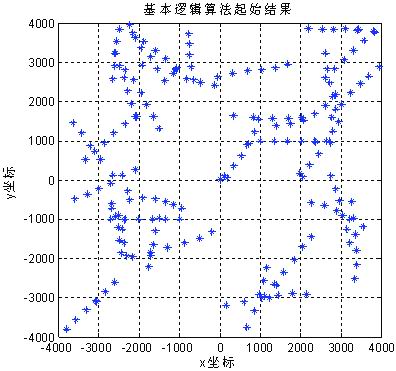
圖2 基本邏輯法起始結果

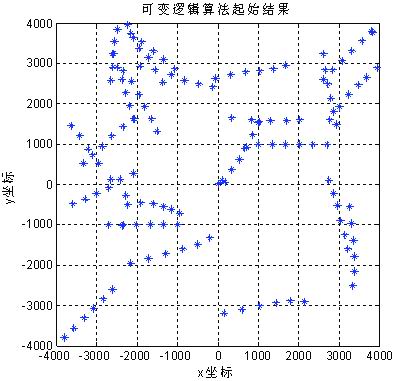
圖3 文章算法起始結果

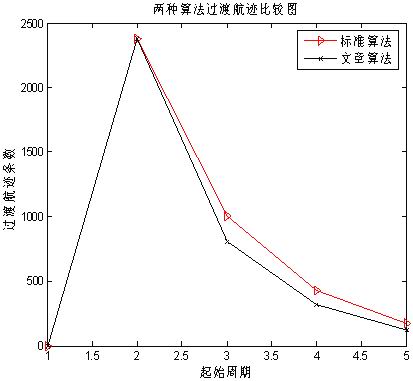
圖4 兩種算法過渡航跡數比較

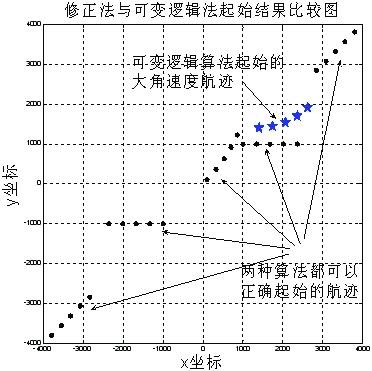
圖5 修正法與可變邏輯法起始結果比較圖

3 過渡航跡數的抑制
盡管在m/m邏輯下，文章算法相比于基本算法的航跡檢測概率改善效果不是很明顯，但是在延遲算法中，每個周期內的點的確定需要下個周期測量結果的確認，則過渡航跡數量會明顯降低。

以第三周期為例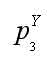，為延遲算法三個點的過渡航跡檢測概率，P3為普通算法的三個點的過渡航跡檢測概率，可得：
P3＝Pd2Pd3??????????????? （9）
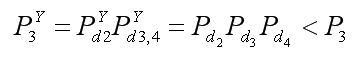?? （10）
同理，在m周期內的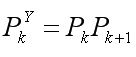，所以本文的一步延遲算法可以明顯降低過渡航跡數。

4 仿真二
在仿真一待起始航跡中，每周期加入參數為20的泊松分布噪聲，即期望個數為20/km2。圖4為5/5標準邏輯法和本文算法的過渡航跡數。
由仿真可以看出，本文算法比基本算法的過渡航跡數明顯降低。

5 大角度航跡的檢測效果
由修正算法的角度關聯門定義可知，如果需要對大角速度的航跡進行檢測，則需要擴大對航跡角度的限制。

在實際情況中，空間航跡呈直線型的概率遠遠大于曲線型，為了檢測到大角度航跡，擴大角度的限制，會造成過渡航跡過多，增大了假航跡起始概率。

可變邏輯的算法，首先檢測目標直線運動的可能性，對于直線起始成功的，就不做曲線判斷；否則，擴大關聯區域進行檢測。其可以在不提高算法復雜度的情況下，對大角度航跡進行監測。

6 仿真三
在仿真一待起始航跡中，每周期加入參數為1的泊松分布噪聲，即期望個數為1/km2。圖5為5/5修正邏輯法（角度限制為0.11rad/s）和本文算法（角度限制為0.05rad/s）的檢測結果。由圖5可知，對于角速度為0.2rad/s的航跡，本文算法可以順利檢測，而修正算法不能檢測。

結論
可變邏輯的航跡起始算法，可以根據不同情況采用相應檢測邏輯。在降低過渡航跡數的同時，提高對大角度航跡的檢測概率。數學推導和仿真均證實了該方法的優勢。