K-means算法是最簡單的一種聚類算法。算法的目的是使各個樣本與所在類均值的誤差平方和達(dá)到最小（這也是評價K-means算法最后聚類效果的評價標(biāo)準(zhǔn)）

　　K-means聚類算法的一般步驟：

　　初始化。輸入基因表達(dá)矩陣作為對象集X，輸入指定聚類類數(shù)N，并在X中隨機(jī)選取N個對象作為初始聚類中心。設(shè)定迭代中止條件，比如最大循環(huán)次數(shù)或者聚類中心收斂誤差容限。

　　進(jìn)行迭代。根據(jù)相似度準(zhǔn)則將數(shù)據(jù)對象分配到最接近的聚類中心，從而形成一類。初始化隸屬度矩陣。

　　更新聚類中心。然后以每一類的平均向量作為新的聚類中心，重新分配數(shù)據(jù)對象。

　　反復(fù)執(zhí)行第二步和第三步直至滿足中止條件。

　　K-均值聚類法的概述

　　之前在參加數(shù)學(xué)建模的過程中用到過這種聚類方法，但是當(dāng)時只是簡單知道了在matlab中如何調(diào)用工具箱進(jìn)行聚類，并不是特別清楚它的原理。最近因?yàn)樵趯W(xué)模式識別，又重新接觸了這種聚類算法，所以便仔細(xì)地研究了一下它的原理。弄懂了之后就自己手工用matlab編程實(shí)現(xiàn)了，最后的結(jié)果還不錯，嘿嘿~~~

　　簡單來說，K-均值聚類就是在給定了一組樣本（x1， x2， 。。.xn） （xi， i = 1， 2， 。。。 n均是向量） 之后，假設(shè)要將其聚為 m（《n） 類，可以按照如下的步驟實(shí)現(xiàn)：

　　Step 1： 從 （x1， x2， 。。.xn） 中隨機(jī)選擇 m 個向量（y1，y2，。。.ym） 作為初始的聚類中心（可以隨意指定，不在n個向量中選擇也可以）;

　　Step 2： 計算 （x1， x2， 。。.xn） 到這 m 個聚類中心的距離（嚴(yán)格來說為 2階范數(shù)）;

　　Step 3： 對于每一個 xi（i = 1，2，。。.n）比較其到 （y1，y2，。。.ym） 距離，找出其中的最小值，若到 yj 的距離最小，則將 xi 歸為第j類;

　　Step 4： m 類分好之后， 計算每一類的均值向量作為每一類新的聚類中心;

　　Step 5： 比較新的聚類中心與老的聚類中心之間的距離，若大于設(shè)定的閾值，則跳到 Step2; 否則輸出分類結(jié)果和聚類中心，算法結(jié)束。

　　單介紹下kmeans算法流程：

　　假設(shè)要把樣本集分為c個類別，算法描述如下：

　　（1）適當(dāng)選擇c個類的初始中心；

　　（2）在第k次迭代中，對任意一個樣本，求其到c各中心的距離，將該樣本歸到距離最短的中心所在的類；

　　（3）利用均值等方法更新該類的中心值；

　　（4）對于所有的c個聚類中心，如果利用（2）（3）的迭代法更新后，值保持不變，則迭代結(jié)束，否則繼續(xù)迭代。

　　該算法的最大優(yōu)勢在于簡潔和快速。算法的關(guān)鍵在于初始中心的選擇和距離公式。

　　matlab實(shí)現(xiàn)：

　　function ［ class count］=k_means（data，k）;

　　%clear

　　%load testdata.mat

　　%k=2;

　　sum=size（data，1）;

　　for i=1:k

　　centroid（i，：）=data（floor（sum/k）*（i-1）+1，：）;

　　end

　　tic

　　ck=0;

　　while 1

　　temp=zeros（1，2）;;

　　count=zeros（1，k）;

　　ck=ck+1

　　for i=1:sum

　　for j=1:k

　　dist（j）=norm（data（i，：）-centroid（j，：））;

　　end

　　［a min_dist］=min（dist）;

　　count（min_dist）=count（min_dist）+1;

　　class（min_dist，count（min_dist））=i;

　　end

　　%重新計算類中心

　　for i=1:k

　　for j=1:count（i）

　　temp=temp+data（class（i，j），：）;

　　end

　　temp_centroid（i，：）=temp/（count（i））;

　　temp（1，：）=0;

　　% temp_centroid（i，：）=re_calculate（class（i，：），count（i），tdata）;

　　end

　　%計算新的類中心和原類中心距離centr_dist;

　　for i=1:k

　　centr_dist（i）=norm（temp_centroid（i，：）-centroid（i，：））;

　　end

　　if max（centr_dist）《=0

　　break;

　　else

　　for i=1:k

　　centroid（i，：）=temp_centroid（i，：）;

　　%重新進(jìn)行前倆不

　　end

　　end

　　end

　　toc

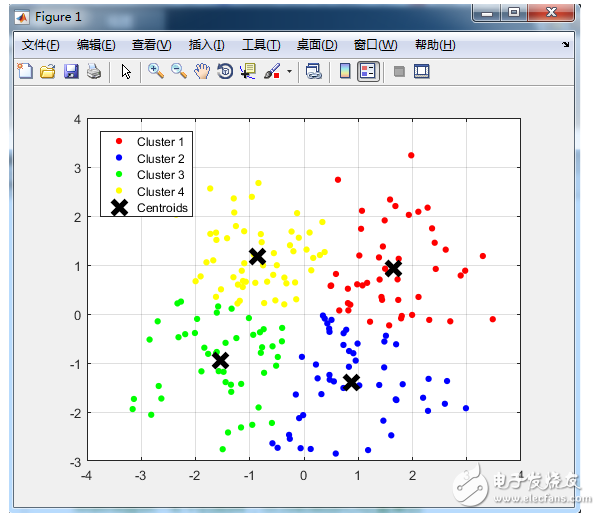
　　數(shù)據(jù)點(diǎn)是鼠標(biāo)插進(jìn)去的，通過界面可以很清晰的看到分類過程，功能截圖如下：

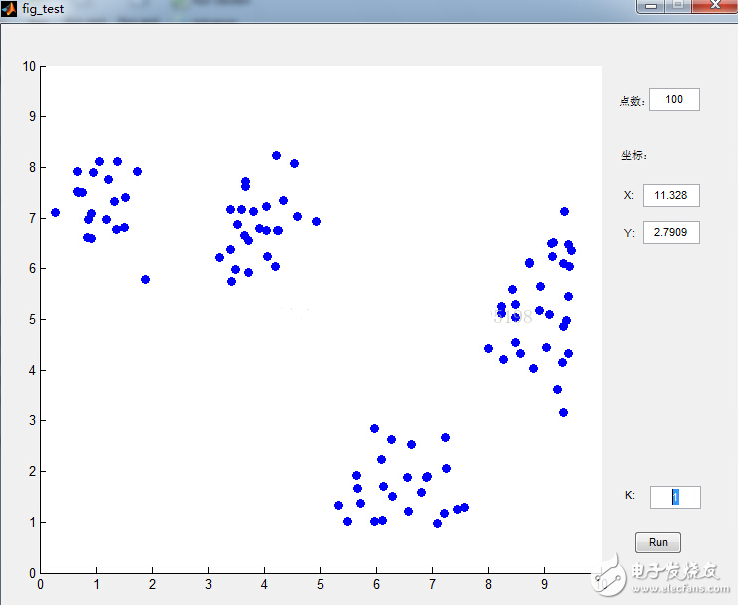
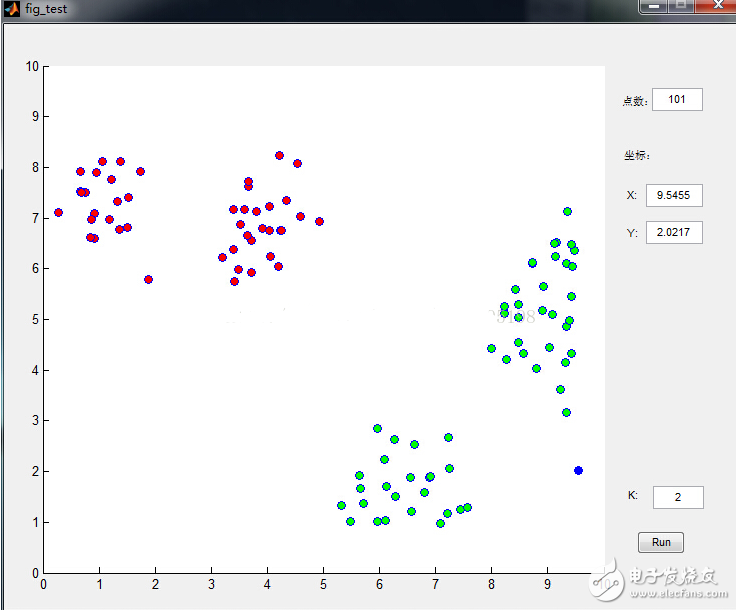
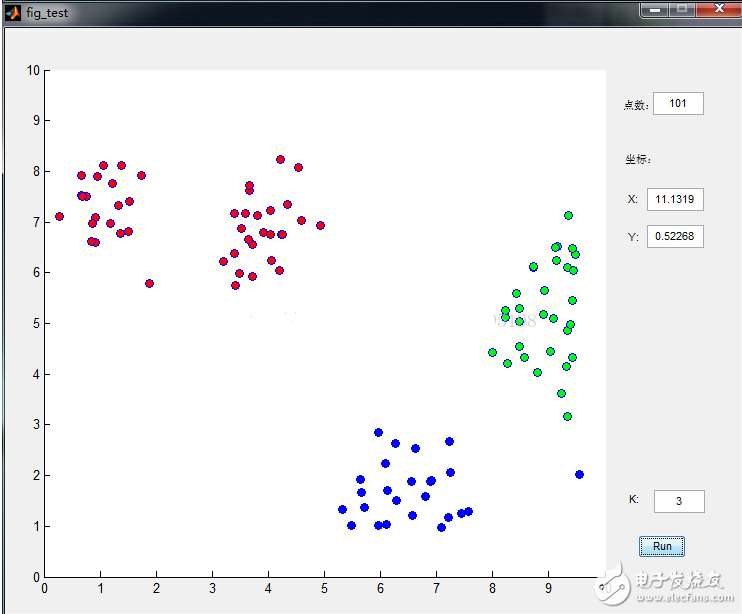
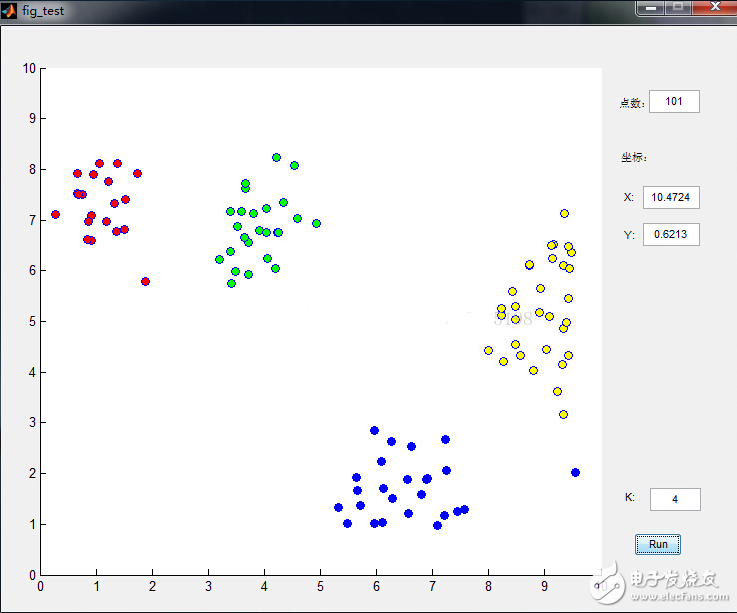
　　下面來看看K-means是如何工作的：

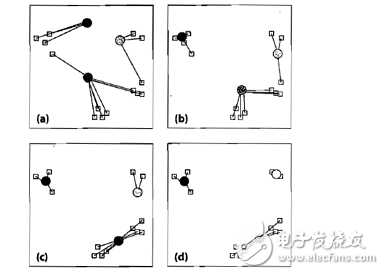
　　圖中圓形為聚類中心，方塊為待聚類數(shù)據(jù)，步驟如下：

　　（a）選取聚類中心，可以任意選取，也可以通過直方圖進(jìn)行選取。我們選擇三個聚類中心，并將數(shù)據(jù)樣本聚到離它最近的中心；

　　（b）數(shù)據(jù)中心移動到它所在類別的中心；

　　（c）數(shù)據(jù)點(diǎn)根據(jù)最鄰近規(guī)則重新聚到聚類中心；

　　（d）再次更新聚類中心；不斷重復(fù)上述過程直到評價標(biāo)準(zhǔn)不再變化

　　評價標(biāo)準(zhǔn)：

　　假設(shè)有M個數(shù)據(jù)源，C個聚類中心。μc為聚類中心。該公式的意思也就是將每個類中的數(shù)據(jù)與每個聚類中心做差的平方和，J最小，意味著分割的效果最好。

　　K-means面臨的問題以及解決辦法：

　　1.它不能保證找到定位聚類中心的最佳方案，但是它能保證能收斂到某個解決方案（不會無限迭代）。

　　解決方法：多運(yùn)行幾次K-means，每次初始聚類中心點(diǎn)不同，最后選擇方差最小的結(jié)果。

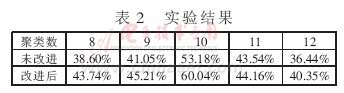
　　2.它無法指出使用多少個類別。在同一個數(shù)據(jù)集中，例如上圖例，選擇不同初始類別數(shù)獲得的最終結(jié)果是不同的。

　　解決方法：首先設(shè)類別數(shù)為1，然后逐步提高類別數(shù)，在每一個類別數(shù)都用上述方法，一般情況下，總方差會很快下降，直到到達(dá)一個拐點(diǎn)；這意味著再增加一個聚類中心不會顯著減少方差，保存此時的聚類數(shù)。

　　MATLAB函數(shù)Kmeans

　　使用方法：

　　Idx=Kmeans（X，K）

　　［Idx，C］=Kmeans（X，K）

　　［Idx，C，sumD］=Kmeans（X，K）

　　［Idx，C，sumD，D］=Kmeans（X，K）

　　［…］=Kmeans（…，’Param1’，Val1，’Param2’，Val2，…）

　　各輸入輸出參數(shù)介紹：

　　X： N*P的數(shù)據(jù)矩陣，N為數(shù)據(jù)個數(shù)，P為單個數(shù)據(jù)維度

　　K： 表示將X劃分為幾類，為整數(shù)

　　Idx： N*1的向量，存儲的是每個點(diǎn)的聚類標(biāo)號

　　C： K*P的矩陣，存儲的是K個聚類質(zhì)心位置

　　sumD： 1*K的和向量，存儲的是類間所有點(diǎn)與該類質(zhì)心點(diǎn)距離之和

　　D： N*K的矩陣，存儲的是每個點(diǎn)與所有質(zhì)心的距離

　　［…］=Kmeans（…，‘Param1’，Val1，‘Param2’，Val2，…）

　　這其中的參數(shù)Param1、Param2等，主要可以設(shè)置為如下：

　　1. ‘Distance’（距離測度）

　　‘sqEuclidean’ 歐式距離（默認(rèn)時，采用此距離方式）

　　‘cityblock’ 絕度誤差和，又稱：L1

　　‘cosine’ 針對向量

　　‘correlation’ 針對有時序關(guān)系的值

　　‘Hamming’ 只針對二進(jìn)制數(shù)據(jù)

　　2. ‘Start’（初始質(zhì)心位置選擇方法）

　　‘sample’ 從X中隨機(jī)選取K個質(zhì)心點(diǎn)

　　‘uniform’ 根據(jù)X的分布范圍均勻的隨機(jī)生成K個質(zhì)心

　　‘cluster’ 初始聚類階段隨機(jī)選擇10%的X的子樣本（此方法初始使用’sample’方法）

　　matrix 提供一K*P的矩陣，作為初始質(zhì)心位置集合

　　3. ‘Replicates’（聚類重復(fù)次數(shù)） 整數(shù)

　　使用案例：

　　data=

　　5.0 3.5 1.3 0.3 -1

　　5.5 2.6 4.4 1.2 0

　　6.7 3.1 5.6 2.4 1

　　5.0 3.3 1.4 0.2 -1

　　5.9 3.0 5.1 1.8 1

　　5.8 2.6 4.0 1.2 0

　　［Idx，C，sumD，D］=Kmeans（data，3，‘dist’，‘sqEuclidean’，‘rep’，4）

　　運(yùn)行結(jié)果：

　　Idx =

　　1

　　2

　　3

　　1

　　3

　　2

　　C =

　　5.0000 3.4000 1.3500 0.2500 -1.0000

　　5.6500 2.6000 4.2000 1.2000 0

　　6.3000 3.0500 5.3500 2.1000 1.0000

　　sumD =

　　0.0300

　　0.1250

　　0.6300

　　D =

　　0.0150 11.4525 25.5350

　　12.0950 0.0625 3.5550

　　29.6650 5.7525 0.3150

　　0.0150 10.7525 24.9650

　　21.4350 2.3925 0.3150

　　10.2050 0.0625 4.0850