根據全加器的定義可知：

輸入為：A，B，Ci其中A，B為被加數和加數，Ci為低位進位數。

輸出為：S，Co，其中S為本位和數，Co為高位進位數。

其邏輯關系為：

S=A⊕B⊕Ci

Co=AB+（A⊕B）Ci

計算后，結果用最小項表示為：

S=m1+m2+m4+m7

Co=m3+m5+m6+m7

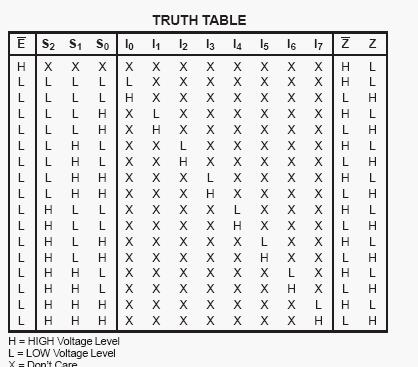
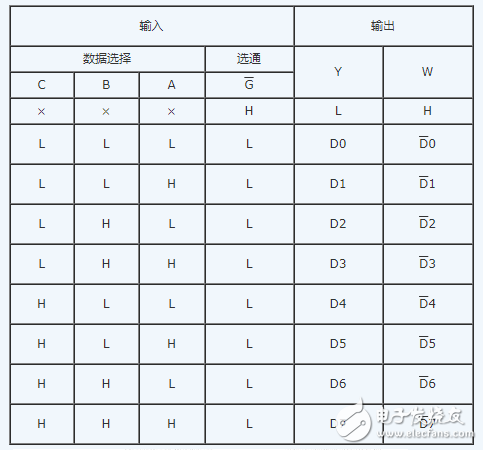
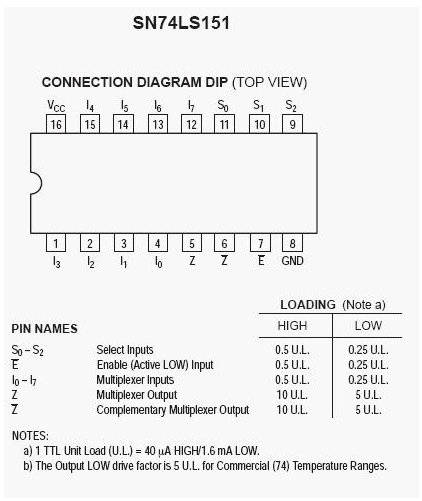
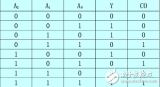
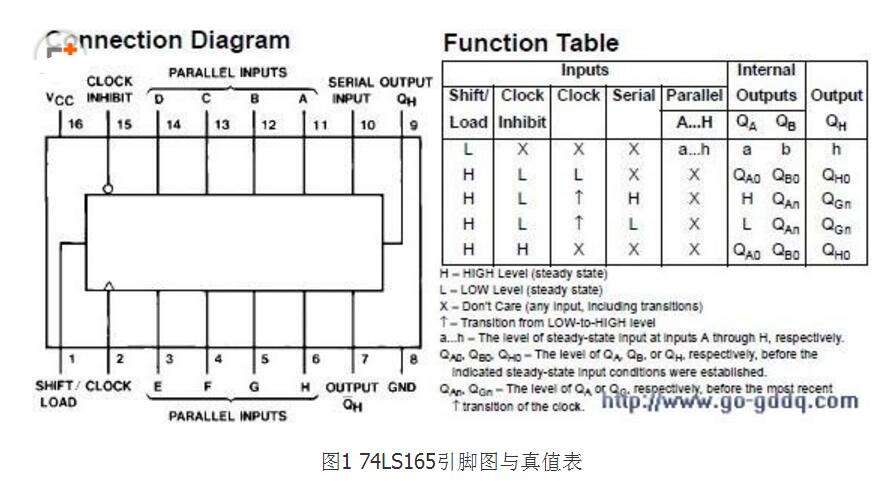
查詢74LS151和74LS138的真值表可知：

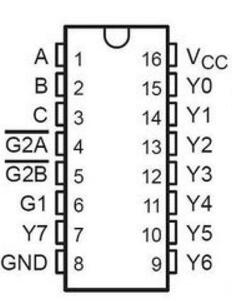
（一）74LS138

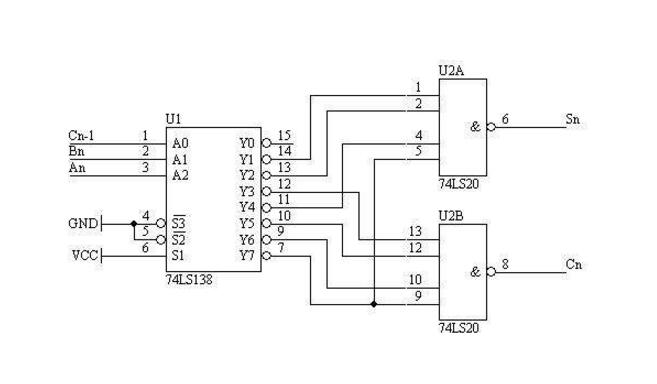
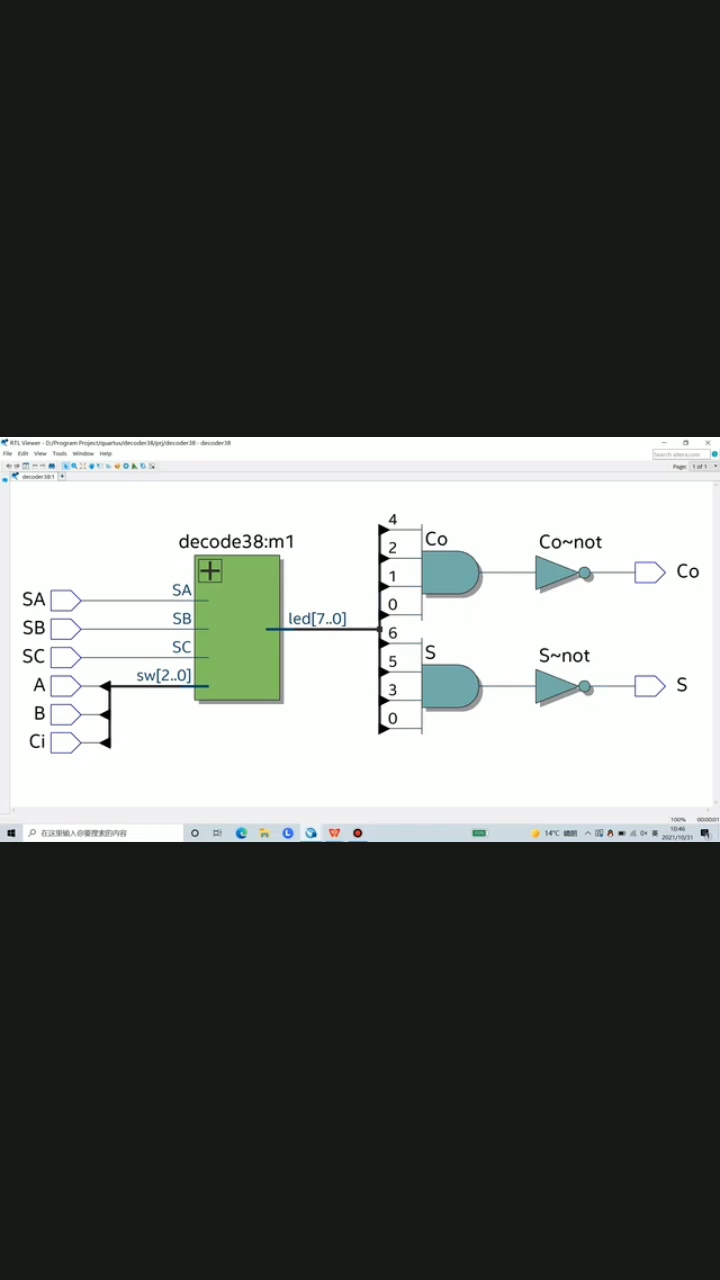
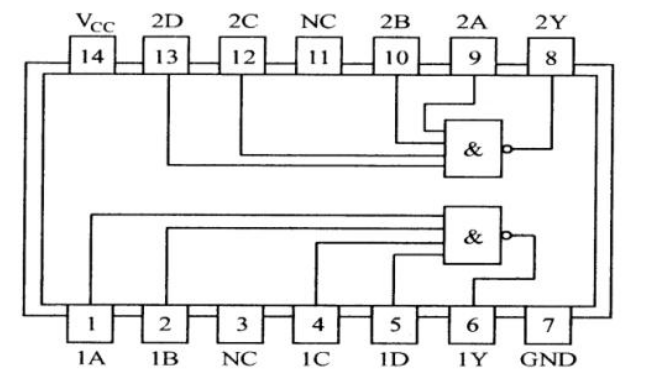
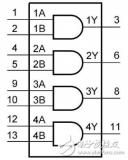
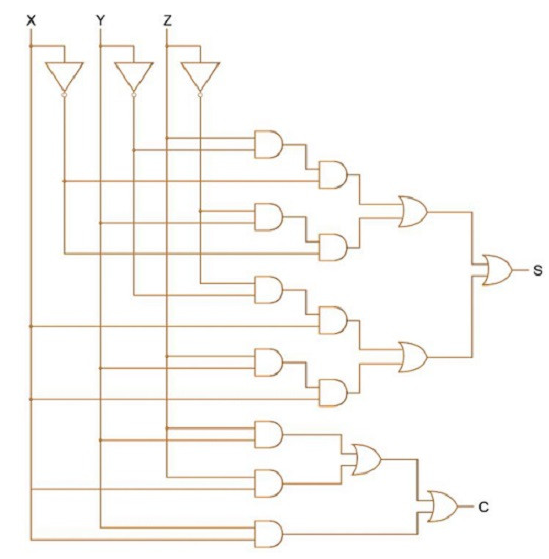
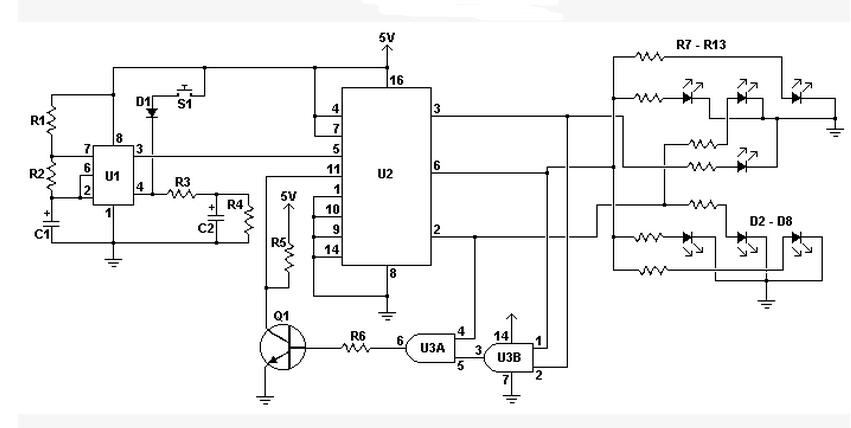
那么利用74LS138可以得到地址端A，B，Ci對應的所有最小項，然后用兩個4輸入與非門（74LS20）取得與上面計算得到的對應的最小項和，就能得到想要的結果。可以設計如圖1所示電路：

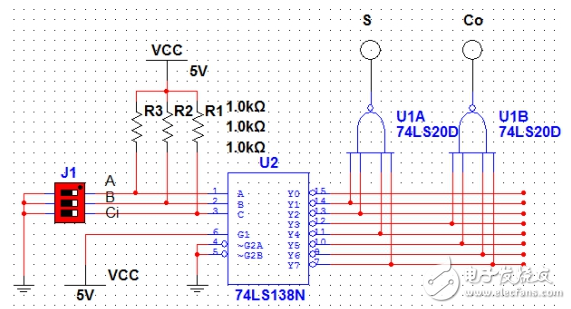
圖1

圖中，三位撥碼開關分別代表A，B和Ci。S和Co是兩個燈，代表S和Co的狀態，為“1”

時亮，為“0”時不亮。

下面給出｛A=1，B=0，Ci=0｝；｛A=0，B=1，Ci=0｝；｛A=1，B=1，Ci=0｝和｛A=1，B=1，Ci=1｝四種輸入狀態下的S和Co狀態。

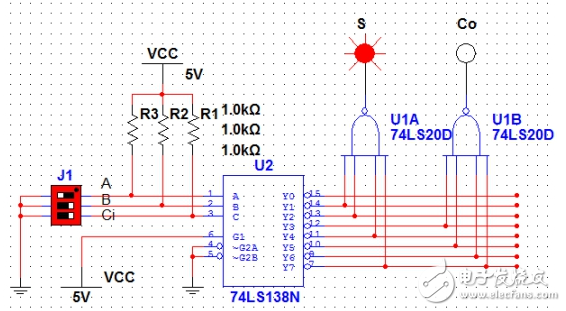
圖2（A=1，B=0，Ci=0）

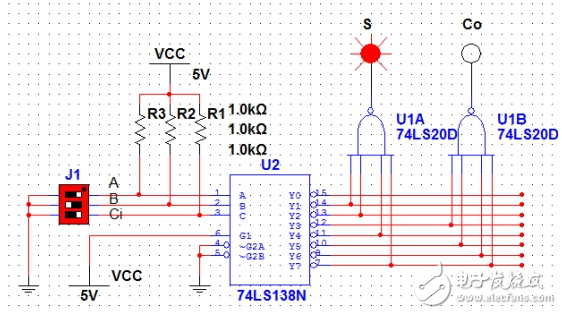
圖3（A=0，B=1，Ci=0）

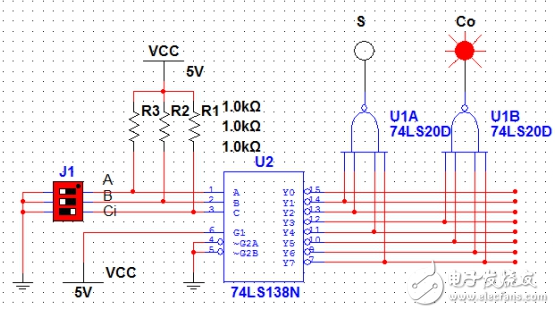
圖4（A=1，B=1，Ci=0）

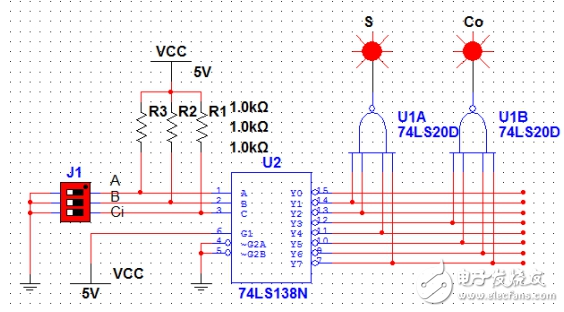
圖5（A=1，B=1，Ci=1）

可以看出電路的邏輯關系是正確的。

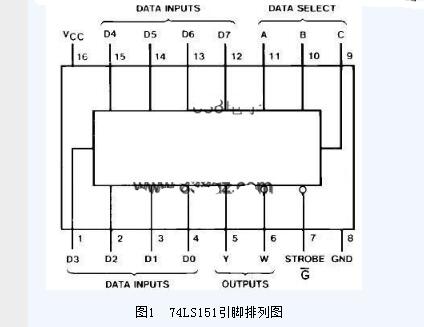
（2）74LS151

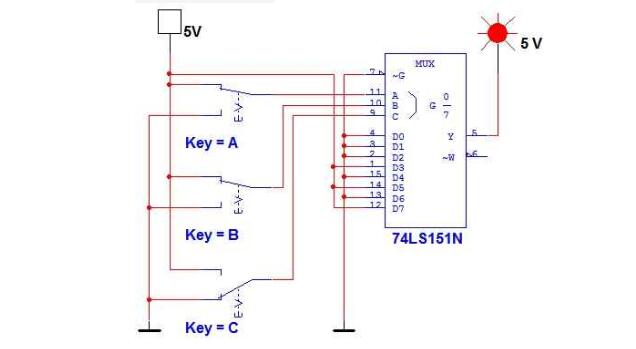
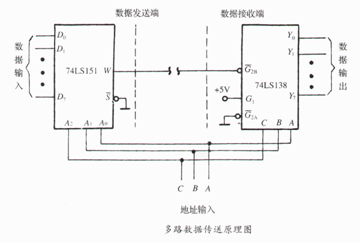
利用74LS151數據選擇器可以設計如圖6所示電路：

兩個74LS151分別得到S和Co；其中U1的數據端配置為D1=D2=D4=D7=1，其余為0；

U2配置為D3=D5=D6=D7=1，其余為0.

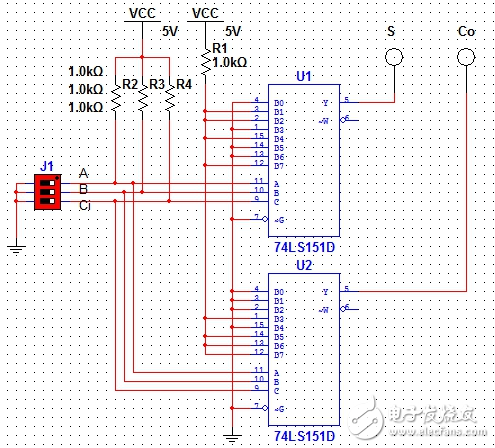
圖6

同樣，下面也給出{A=1，B=0，Ci=0}；｛A=0，B=1，Ci=0｝；｛A=1，B=1，Ci=0｝和｛A=1，B=1，Ci=1｝四種輸入狀態下的S和Co狀態。

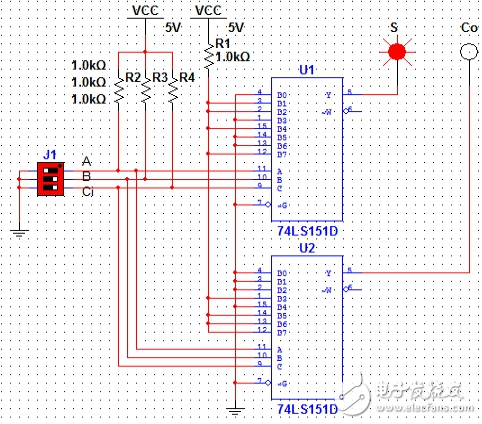
圖7（A=1，B=0，Ci=0）

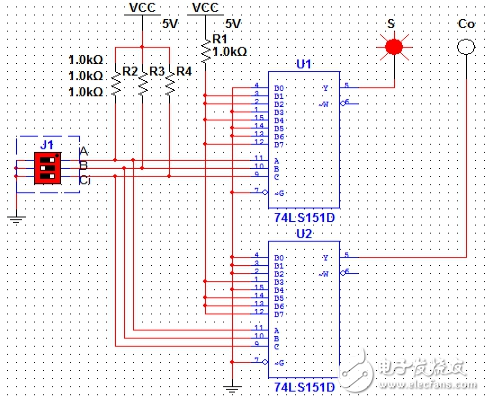
圖8（A=0，B=1，Ci=0）

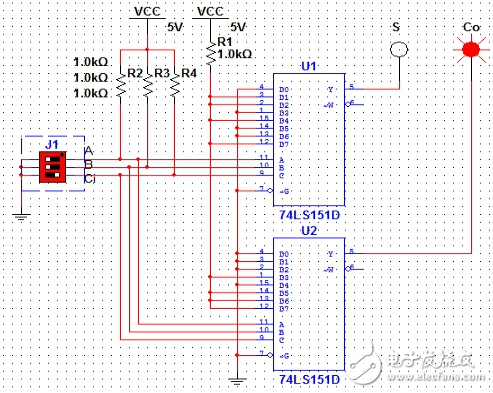
圖9（A=1，B=1，Ci=0）

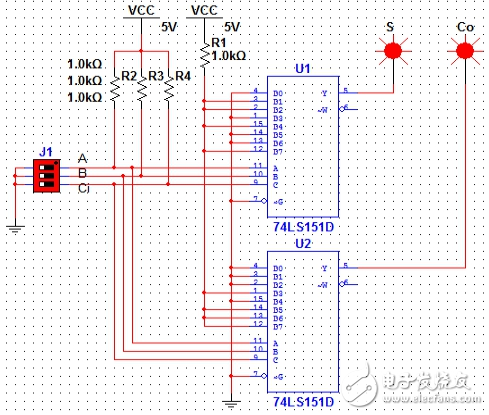
圖10（A=1，B=1，Ci=1）

可以看出，電路的邏輯關系也是正確的。