| 如前所述,頻率特性法是一種工程方法,主要采用的是一種圖解法。常用的頻率特性圖示方法分兩種:極坐標圖示法、對數坐標圖示法。本節介紹極坐標圖示法。
由于頻率特性 是一個復數,因而可在復平面上用直角坐標形式表示:
同樣也可用極坐標形式寫成:
式中,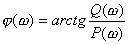 。這樣, 可用幅值為 、相角為 的向量來表示。當輸入信號的頻率ω由 變化時,向量 的幅值和相位也隨之作相應的變化,其端點在復平面上移動而形成的軌跡曲線,稱為極坐標圖,又稱為 。這樣, 可用幅值為 、相角為 的向量來表示。當輸入信號的頻率ω由 變化時,向量 的幅值和相位也隨之作相應的變化,其端點在復平面上移動而形成的軌跡曲線,稱為極坐標圖,又稱為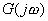 的幅相特性或奈奎斯特(Nyquist)曲線,簡稱奈氏圖。 的幅相特性或奈奎斯特(Nyquist)曲線,簡稱奈氏圖。
5.2.1 典型環節的奈氏曲線
為了便于對頻率特性作圖,本章中的開環傳遞函數均以時間常數形式表示。具有這種形式的開環頻率特性 一般由下列五種典型環節組成。
1)比例環節K;
2)一階環節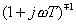 ; ;
3)積分和微分環節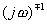 ; ;
4)二階環節  ; ;
5)延遲環節 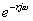 。 。
1.比例環節
比例環節的頻率特性為
由于K是一個與ω無關的常數,它的相角為零度,因而它的奈氏圖為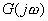 復平面實軸上的一個定點,如圖5-5所示。 復平面實軸上的一個定點,如圖5-5所示。
2.積分和微分環節
積分環節的頻率特性為
由上式可見,積分環節的幅值與ω成反比,相角恒為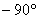 ,其奈氏圖如圖5-6a所示。顯然積分環節是一個相位滯后環節,每當信號經過一個積分環節后,其相位滯后 ,其奈氏圖如圖5-6a所示。顯然積分環節是一個相位滯后環節,每當信號經過一個積分環節后,其相位滯后 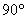 。 。
對于微分環節,其頻率特性為
它的奈氏圖應如圖5-6b所示。由圖可見,微分環節是一個相位超前環節,每當系統增加一個微分環節,將使相位增加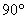 。 。
比較積分環節和微分環節可以發現,它們的幅值特性和相位特性均剛剛相反。
3.一階慣性環節
一階慣性環節的頻率特性為
式中, 
若將上式寫成實頻特性和虛頻特性的形式:
式中
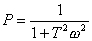 , ,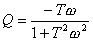 |
于是得
也即
顯然上式是一個圓的方程,其圓心為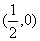 ,半徑為 ,半徑為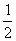 ,如圖5-7a所示。可見,一階慣性環節是一個相位滯后環節,其最大滯后角為 ,如圖5-7a所示。可見,一階慣性環節是一個相位滯后環節,其最大滯后角為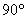 ,此時頻率為無窮大。 ,此時頻率為無窮大。
一階微分環節的頻率特性為
式中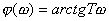 。當 。當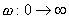 時,其幅值從 時,其幅值從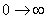 ,相角 ,相角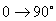 ,因此它是一個相位超前環節。圖5-7b為它的奈氏圖。 ,因此它是一個相位超前環節。圖5-7b為它的奈氏圖。
4.二階振蕩環節和二階微分環節
根據第三章內容,典型二階振蕩環節的頻率特性可寫為
式中
由式(5-28)可知,振蕩環節奈氏圖的低頻段和高頻段分別為
當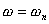 時, 時,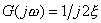 ,其相角為 ,其相角為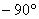 。 。
當ξ值已知,則由式(5-28)可求得對應于不同ω值時的 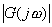 和 和 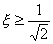 值。圖5-8為式(5-28)在不同ξ值下用Matlab繪制的奈氏曲線。當 值。圖5-8為式(5-28)在不同ξ值下用Matlab繪制的奈氏曲線。當 時,在奈氏曲線上距原點最遠的點所對應的頻率就是振蕩環節的諧振頻率 時,在奈氏曲線上距原點最遠的點所對應的頻率就是振蕩環節的諧振頻率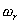 ,其諧振峰值 ,其諧振峰值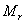 用 用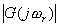 與 與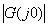 之比來表示。 之比來表示。
由第三章的討論可知,當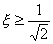 時,振蕩環節不產生諧振, 時,振蕩環節不產生諧振, 向量的長度將隨著ω的增加而單調地減小。當 向量的長度將隨著ω的增加而單調地減小。當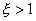 時, 時, 有兩個相異的實數極點。如果ξ值足夠大,則其中一個極點靠近s平面的坐標原點,另一個極點遠離虛軸。顯然,遠離虛軸的這個極點對瞬態響應的影響很小,此時式(5-28)的特性與一階慣性環節相類同,它的奈氏圖近似于一個半圓。 有兩個相異的實數極點。如果ξ值足夠大,則其中一個極點靠近s平面的坐標原點,另一個極點遠離虛軸。顯然,遠離虛軸的這個極點對瞬態響應的影響很小,此時式(5-28)的特性與一階慣性環節相類同,它的奈氏圖近似于一個半圓。
二階微分環節的頻率特性為
式中
圖5-9為二階微分環節的奈氏圖。
5.時滯環節
時滯環節的頻率特性為
由于時滯環節的幅頻值恒為1,而其相位與ω成比例變化,因而它的奈氏圖是一個單位圓,如圖5-10所示。在低頻區,時滯環節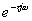 和慣性環節 和慣性環節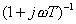 的頻率特性很接近,如圖5-11所示。因為 的頻率特性很接近,如圖5-11所示。因為
當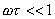 時,上式可近似為 時,上式可近似為
| 圖5-11時滯環節與下一階慣性環節在低頻段的等效性 |
因此當 時,時滯環節通常近似地可用慣性環節表示。 時,時滯環節通常近似地可用慣性環節表示。
5.2.2 開環系統的奈奎斯特圖
在采用頻率特性法對控制系統進行分析時,一般采用兩種方法:一種是直接采用開環頻率特性分析閉環系統的性能,另外一種是根據開環頻率特性曲線繪制閉環頻率特性,然后用閉環頻率特性分析閉環系統的性能。但不論采用哪一種方法,在用極坐標圖進行分析時,首先應作出極坐標形式的開環幅值特性和開環相位特性曲線。
對于如圖5-12的閉環控制系統,其開環傳遞函數為 ,把開環頻率特性寫作如下的極坐標形式或直角坐標形式: ,把開環頻率特性寫作如下的極坐標形式或直角坐標形式:
當ω由 變化時,逐點計算相應的 和 的值,可畫出開環系統的奈氏圖。在控制工程中,一般只需畫出奈氏曲線的大致形狀和幾個關鍵點的位置,如與實軸相交點、與慮軸相交點及曲線的旋轉方向等,即可對控制系統進行分析。
例5-2 試繪制下列開環傳遞函數的奈奎斯特曲線:
試繪制下列開環傳遞函數的奈奎斯特曲線:
解:該開環系統由三個典型環節串聯組成:一個比例環節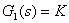 、兩個一階慣性環節 、兩個一階慣性環節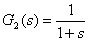 和 和 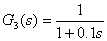 。這三個環節的幅、相頻率特性分別為: 。這三個環節的幅、相頻率特性分別為:
因而開環系統的幅頻特性:
相頻特性:
取不同的頻率 值,可得到對應的幅值和相角,根據這些值可繪制出開環系統的奈氏圖如圖5-13。
事實上,在Matlab中,有專門的函數用于繪制開環系統的極坐標圖:Nyquist。關于該命令的詳細說明,可見第九章說明。對于本題,可用如下命令:
g=tf(10,conv([1,1],[0.1,1]))
Transfer function:
10
-------------------
0.1 s^2 + 1.1 s + 1
nyquist(g)
在實際的控制系統中,開環傳遞函數常常由若干典型環節串聯而成,因此通過對典型系統的奈氏圖的繪制將有助于用奈氏圖分析和設計控制系統。下面通過對不同類型系統的奈氏圖在 和 時特征的分析,簡要研究控制系統的靜態和動態性能。
1.0型系統
設0型系統的開環頻率特性為
當 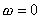 時, 時,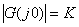 、 、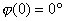 ,即為實軸上的一點(K,0),它是0型系統奈氏圖的始點。當 ,即為實軸上的一點(K,0),它是0型系統奈氏圖的始點。當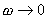 時, 時,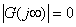 、 、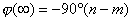 。當 。當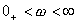 時,奈氏曲線的具體形狀由開環傳遞函數所含的具體環節和參數所確定。 時,奈氏曲線的具體形狀由開環傳遞函數所含的具體環節和參數所確定。
2.I型系統
設I型系統的開環頻率特性為
由上式不難看出,當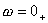 時, 時,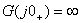 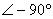 ;當 ;當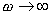 時, 時,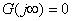 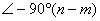 。 。
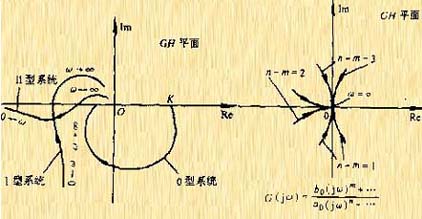
| 圖5-14a 0型、1型和II型系統的奈氏圖 |
圖5-14b 開環系統高頻段的奈氏圖 |
? | | |
3、Ⅱ型系統
設Ⅱ型系統的開環頻率特性為
由式(5-36)可知,當 時, 時,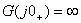 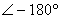 ;當 ;當 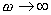 時, 時,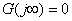 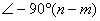 。 。
綜上所述,開環系統極坐標圖的低頻部分是由因式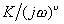 確定的。對于0型系統, 確定的。對于0型系統,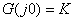 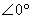 ;而對于I型和I型以上的 型系統, ;而對于I型和I型以上的 型系統,
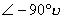 。如果 。如果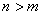 ,當 ,當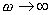 時, 時,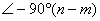 , ,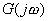 曲線以順時針方向按 的角度趨向于坐標原點,如果(n-m)是偶數,則曲線與橫軸相切;反之,若是奇數,則曲線與虛軸相切。圖5-14a為0型、I型和Ⅱ型系統的奈氏圖。圖5-14b為高頻段的奈氏圖。 曲線以順時針方向按 的角度趨向于坐標原點,如果(n-m)是偶數,則曲線與橫軸相切;反之,若是奇數,則曲線與虛軸相切。圖5-14a為0型、I型和Ⅱ型系統的奈氏圖。圖5-14b為高頻段的奈氏圖。
例5-3 已知0型系統、I型系統和II型系統的開環傳遞函數分別為....
已知0型系統、I型系統和II型系統的開環傳遞函數分別為
試繪制它們對應的奈氏圖。
解 (1)0型系統的頻率特性為
| 式中, |
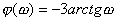 , , |
分別取 ,由上述兩式,計算不同ω值時的 和 。據此,可得到圖5-15所示的奈氏圖。根據第三章勞斯判據可知,當 ,閉環系統穩定,表現在奈氏圖上是極坐標圖不包圍(-1,j0),這與后面將介紹的奈氏穩定判據是一致的。
(2)I型系統的頻率特性為
| 其中 |
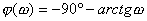 , , |
把上式改寫為
上式中,當 時, ,即 ;當 時, 。據此畫出圖5-16所示的奈氏圖。
(3)該Ⅱ型系統的開環頻率特性為
據此畫出圖5-17所示的奈氏圖。
由于采用了Matlab,對于I、II型系統,在無窮遠處的極坐標無法在圖中標明,但從圖中同樣可以看到,當頻率接近零時,極坐標曲線漸近于平行于虛軸的-10,這一點可將幅值頻率特性寫成實頻、虛頻形式得到驗證。
|  電子發燒友App
電子發燒友App

 硬聲App
硬聲App

 56
56
 93
93
 201
201
 354
354
 2199
2199
 599
599
 235
235
 19
19 4849
4849
 12
12 9018
9018
 3501
3501
 7225
7225
 19225
19225 2677
2677
 70420
70420
 45632
45632
 12517
12517
 15413
15413
 26893
26893
 4
4 732
732 9966
9966 31
31 16
16 78
78 2197
2197 1578
1578
 31
31 23
23 2093
2093
評論