Kirchhoffs電路法允許我們通過為電路周圍的電壓和電流定義一組基本網(wǎng)絡(luò)定律和定理來解決復(fù)雜的電路問題。

我們在電阻器教程中看到了一個當(dāng)兩個或多個電阻串聯(lián)，并聯(lián)或兩者結(jié)合在一起時，可以找到等效電阻（R T ），并且這些電路符合歐姆定律。

然而，有時在橋接或T網(wǎng)絡(luò)等復(fù)雜電路中，我們不能單獨使用歐姆定律來找到電路中循環(huán)的電壓或電流。對于這些類型的計算，我們需要一些允許我們獲得電路方程的規(guī)則，為此我們可以使用Kirchhoffs電路定律。

1845年，德國物理學(xué)家，Gustav Kirchhoff制定了一對或一套規(guī)則或法律，用于處理電路內(nèi)電流和能量的守恒。這兩個規(guī)則通常被稱為：基爾霍夫電路定律，其中一個基爾霍夫定律涉及在閉合電路周圍流動的電流，基爾霍夫電流定律，（KCL）法律涉及閉合電路中存在的電壓源，基爾霍夫電壓定律，（KVL）

基爾霍夫第一定律 - 現(xiàn)行定律，（KCL）

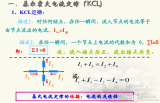
基爾霍夫電流定律或KCL，指出“進入結(jié)點或節(jié)點的總電流或電荷與離開節(jié)點的電荷完全相同，因為它沒有其它地方可去離開，因為節(jié)點內(nèi)沒有任何費用“。換句話說，進入和離開節(jié)點的所有電流的代數(shù)和必須等于零，I （退出） + I （進入） = 0。基爾霍夫的這個想法通常被稱為充電守恒。

基爾霍夫現(xiàn)行法

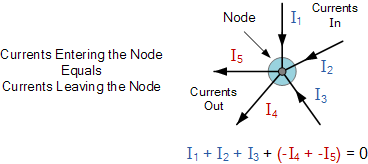
這里，三個電流進入節(jié)點， I 1 ，I 2 ，I 3 值均為正值，離開節(jié)點的兩個電流 I 4 且I 5 值為負值。那么這意味著我們也可以將等式重寫為：

I 1 + I 2 + I 3 -I 4 -I 5 = 0

電路中的術(shù)語節(jié)點一般是指兩個或多個載流路徑或元件（例如電纜和元件）的連接或連接。同樣，為了使電流流入或流出節(jié)點，必須存在閉合電路路徑。我們可以在分析并聯(lián)電路時使用基爾霍夫電流定律。

基爾霍夫第二定律 - 電壓定律，（KVL）

基爾霍夫電壓定律或KVL，狀態(tài)“在任何閉環(huán)網(wǎng)絡(luò)中，環(huán)路周圍的總電壓等于同一環(huán)路內(nèi)所有電壓降的總和”，也等于零。換句話說，環(huán)路內(nèi)所有電壓的代數(shù)和必須等于零。基爾霍夫的這個想法被稱為能量守恒。

基爾霍夫電壓定律

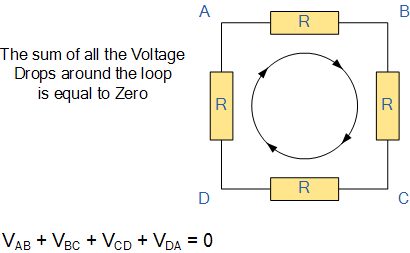
從循環(huán)中的任何一點開始繼續(xù)沿相同方向注意所有電壓下降的方向，無論是正還是負，并返回到相同的起點點。重要的是順時針或逆時針保持相同的方向，否則最終的電壓總和不會等于零。在分析串聯(lián)電路時，我們可以使用基爾霍夫電壓定律。

當(dāng)使用基爾霍夫電路定律分析直流電路或交流電路時，使用了許多定義和術(shù)語來描述部分電路。被分析的電路，例如：節(jié)點，路徑，分支，循環(huán)和網(wǎng)格。這些術(shù)語經(jīng)常用于電路分析，因此了解它們非常重要。

常見的直流電路理論術(shù)語：

?電路 - 電路是電流流過的閉環(huán)導(dǎo)電路徑。

?路徑 - 一行連接元件或源。

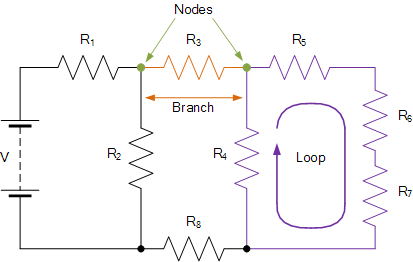
?節(jié)點 - 節(jié)點是電路中的連接點，連接或終端，兩個或多個電路元件連接或連接在一起，在兩個或多個分支之間提供連接點。節(jié)點由點表示。

?分支 - 分支是連接在兩個節(jié)點之間的單個或一組組件，如電阻器或源。

?循環(huán) - 循環(huán)是電路中的一個簡單閉合路徑，其中不會遇到多次電路元件或節(jié)點。

?網(wǎng)格 - 網(wǎng)格是一個沒有封閉路徑的開環(huán)。網(wǎng)格內(nèi)沒有任何組件。

請注意：

如果相同的當(dāng)前值，則稱組件在系列中連接在一起流過所有組件。

如果組件的電壓相同，則稱組件并聯(lián)連接在一起。

典型的直流電路

Kirchhoffs電路定律示例No1

查找40Ω電阻中的電流， R 3

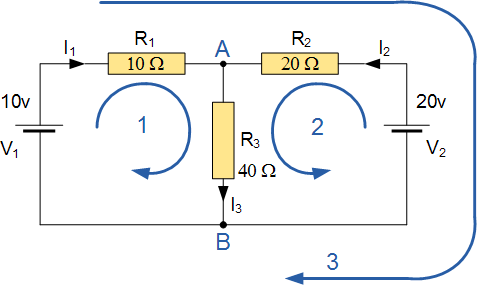
該電路有3個分支，2個節(jié)點（ A 和 B ）和2個獨立循環(huán)。

使用基爾霍夫電流定律，KCL，方程式如下：

節(jié)點 A ： I 1 + I 2 = I 3

在節(jié)點 B ： I 3 = I 1 + I 2

使用基爾霍夫電壓定律，KVL方程式如下：

循環(huán)1的給出如下： 10 = R 1 I 1 + R <子> 3 I <子> 3 = 10I <子> 1 + 40I <子> 3

循環(huán)2的給出如下： 20 = R 2 I 2 + R 3 I 3 = 20I 2 + 40I 3

循環(huán)3的給出如下： 10-20 = 10I 1 -20I 2

as I 3 是<的總和span> I 1 + I 2 我們可以將方程重寫為;

Eq。否1： 10 = 10I 1 +40（I 1 + I 2 ）= 50I 1 + 40I <子> 2

等式No 2： 20 = 20I 2 +40（I 1 + I 2 ）= 40I 1 + 60I 2

我們現(xiàn)在有兩個“聯(lián)立方程式”可以減少給我們 I的值 1 和 I 2

I 1 的替代 I 2 為我們提供 I 1 的值為 -0.143 Amps

用 I 1 替換 I 2 給出我們 I 2 的值為 + 0.429Amps

As： I 3 = I 1 + I 2

流入電阻 R 3 的電流給出如下： -0.143 + 0.429 = 0.286Amps

電阻兩端的電壓 R 3 給出為： 0.286x40 = 11.44volts

I 1 的負號表示當(dāng)前的方向最初選擇的流量是wr ong，但從來沒有那么有效。實際上，20v電池正在為10v電池充電。

Kirchhoffs電路法的應(yīng)用

這兩個法則可以實現(xiàn)電流和電壓在要找到的電路中，即電路被稱為“分析”，使用基爾霍夫電路定律的基本程序如下：

1。假設(shè)給出了所有電壓和電阻。 （如果沒有標記它們 V1，V2，... R1，R2，等）

2。用分支電流標記每個分支。 （ I1，I2，I3 等）

3。查找每個節(jié)點的Kirchhoff第一定律方程。

4.找到基爾霍夫電路中每個獨立回路的第二定律方程。

5.根據(jù)需要使用線性聯(lián)立方程來尋找未知電流。

除了使用基爾霍夫電路定律來計算在線性電路周圍循環(huán)的各種電壓和電流，我們還可以使用環(huán)路分析來計算每個電流和電流。獨立循環(huán)，有助于減少使用基爾霍夫定律所需的數(shù)學(xué)量。在下一個關(guān)于直流電路的教程中，我們將研究網(wǎng)狀電流分析。