當(dāng)貝葉斯、奧卡姆和香農(nóng)一起給機(jī)器學(xué)習(xí)下定義,將統(tǒng)計(jì)學(xué)、信息理論和自然哲學(xué)的一些核心概念結(jié)合起來(lái),我們便會(huì)會(huì)發(fā)現(xiàn),可以對(duì)監(jiān)督機(jī)器學(xué)習(xí)的基本限制和目標(biāo)進(jìn)行深刻而簡(jiǎn)潔的描述。
令人有點(diǎn)驚訝的是,在所有機(jī)器學(xué)習(xí)的流行詞匯中,我們很少聽(tīng)到一個(gè)將統(tǒng)計(jì)學(xué)、信息理論和自然哲學(xué)的一些核心概念融合起來(lái)的短語(yǔ)。
而且,它不是一個(gè)只有機(jī)器學(xué)習(xí)博士和專家懂得的晦澀術(shù)語(yǔ),對(duì)于任何有興趣探索的人來(lái)說(shuō),它都具有精確且易于理解的含義,對(duì)于ML和數(shù)據(jù)科學(xué)的從業(yè)者來(lái)說(shuō),它具有實(shí)用的價(jià)值。
這個(gè)術(shù)語(yǔ)就是最小描述長(zhǎng)度(Minimum Description Length)。
讓我們剝繭抽絲,看看這個(gè)術(shù)語(yǔ)多么有用……
貝葉斯和他的理論
我們從托馬斯·貝葉斯(Thomas Bayes)說(shuō)起,順便一提,他從未發(fā)表過(guò)關(guān)于如何做統(tǒng)計(jì)推理的想法,但后來(lái)卻因“貝葉斯定理”而不朽。
Thomas Bayes
那是在18世紀(jì)下半葉,當(dāng)時(shí)還沒(méi)有一個(gè)數(shù)學(xué)科學(xué)的分支叫做“概率論”。人們知道概率論,是因?yàn)閬啿?· 棣莫弗(Abraham de Moievre)寫(xiě)的《機(jī)遇論》(Doctrine of Chances)一書(shū)。
1763年,貝葉斯的著作《機(jī)會(huì)問(wèn)題的解法》(An Essay toward solving a Problem in the Doctrine of opportunities)被寄給英國(guó)皇家學(xué)會(huì),但經(jīng)過(guò)了他的朋友理查德·普萊斯(Richard Price)的編輯和修改,發(fā)表在倫敦皇家學(xué)會(huì)哲學(xué)匯刊。在那篇文章中,貝葉斯以一種相當(dāng)繁復(fù)的方法描述了關(guān)于聯(lián)合概率的簡(jiǎn)單定理,該定理引起了逆概率的計(jì)算,即貝葉斯定理。
自那以后,統(tǒng)計(jì)科學(xué)的兩個(gè)派別——貝葉斯學(xué)派和頻率學(xué)派(Frequentists)之間發(fā)生了許多爭(zhēng)論。但為了回歸本文的目的,讓我們暫時(shí)忽略歷史,集中于對(duì)貝葉斯推理的機(jī)制的簡(jiǎn)單解釋。請(qǐng)看下面這個(gè)公式:
這個(gè)公式實(shí)際上告訴你,在看到數(shù)據(jù)/證據(jù)(可能性)之后更新你的信念(先驗(yàn)概率),并將更新后的信念程度賦予后驗(yàn)概率。你可以從一個(gè)信念開(kāi)始,但每個(gè)數(shù)據(jù)點(diǎn)要么加強(qiáng)要么削弱這個(gè)信念,你會(huì)一直更新你的假設(shè)。
聽(tīng)起來(lái)十分簡(jiǎn)單而且直觀是吧?很好。
不過(guò),我在這段話的最后一句話里耍了個(gè)小花招。你注意了嗎?我提到了一個(gè)詞“假設(shè)”。
在統(tǒng)計(jì)推理的世界里,假設(shè)就是信念。這是一種關(guān)于過(guò)程本質(zhì)(我們永遠(yuǎn)無(wú)法觀察到)的信念,在一個(gè)隨機(jī)變量的產(chǎn)生背后(我們可以觀察或測(cè)量到隨機(jī)變量,盡管可能有噪聲)。在統(tǒng)計(jì)學(xué)中,它通常被稱為概率分布。但在機(jī)器學(xué)習(xí)的背景下,它可以被認(rèn)為是任何一套規(guī)則(或邏輯/過(guò)程),我們認(rèn)為這些規(guī)則可以產(chǎn)生示例或訓(xùn)練數(shù)據(jù),我們可以學(xué)習(xí)這個(gè)神秘過(guò)程的隱藏本質(zhì)。
因此,讓我們嘗試用不同的符號(hào)重新定義貝葉斯定理——用與數(shù)據(jù)科學(xué)相關(guān)的符號(hào)。我們用D表示數(shù)據(jù),用h表示假設(shè),這意味著我們使用貝葉斯定理的公式來(lái)嘗試確定數(shù)據(jù)來(lái)自什么假設(shè),給定數(shù)據(jù)。我們把定理重新寫(xiě)成:
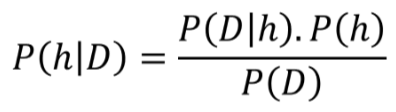
現(xiàn)在,一般來(lái)說(shuō),我們有一個(gè)很大的(通常是無(wú)限的)假設(shè)空間,也就是說(shuō),有許多假設(shè)可供選擇。貝葉斯推理的本質(zhì)是,我們想要檢驗(yàn)數(shù)據(jù)以最大化一個(gè)假設(shè)的概率,這個(gè)假設(shè)最有可能產(chǎn)生觀察數(shù)據(jù)(observed data)。我們一般想要確定P(h|D)的argmax,也就是想知道哪個(gè)h的情況下,觀察到的D是最有可能的。為了達(dá)到這個(gè)目的,我們可以把這個(gè)項(xiàng)放到分母P(D)中,因?yàn)樗灰蕾囉诩僭O(shè)。這個(gè)方案就是最大后驗(yàn)概率估計(jì)(maximum a posteriori,MAP)。
現(xiàn)在,我們應(yīng)用以下數(shù)學(xué)技巧:
最大化對(duì)于對(duì)數(shù)與原始函數(shù)的作用類似,即采用對(duì)數(shù)不會(huì)改變最大化問(wèn)題
乘積的對(duì)數(shù)是各個(gè)對(duì)數(shù)的總和
一個(gè)量的最大化等于負(fù)數(shù)量的最小化

那些負(fù)對(duì)數(shù)為2的術(shù)語(yǔ)看起來(lái)很熟悉是不是......來(lái)自信息論(Information Theory)!
讓我們進(jìn)入克勞德·香農(nóng)(Claude Shannon)的世界吧!
香農(nóng)和信息熵
如果要描述克勞德·香農(nóng)的天才和奇特的一生,長(zhǎng)篇大論也說(shuō)不完。香農(nóng)幾乎是單槍匹馬地奠定了信息論的基礎(chǔ),引領(lǐng)我們進(jìn)入了現(xiàn)代高速通信和信息交流的時(shí)代。
香農(nóng)在MIT電子工程系完成的碩士論文被譽(yù)為20世紀(jì)最重要的碩士論文:在這篇論文中,22歲的香農(nóng)展示了如何使用繼電器和開(kāi)關(guān)的電子電路實(shí)現(xiàn)19世紀(jì)數(shù)學(xué)家喬治布爾(George Boole)的邏輯代數(shù)。數(shù)字計(jì)算機(jī)設(shè)計(jì)的最基本的特征——將“真”和“假”、“0”和“1”表示為打開(kāi)或關(guān)閉的開(kāi)關(guān),以及使用電子邏輯門來(lái)做決策和執(zhí)行算術(shù)——可以追溯到香農(nóng)論文中的見(jiàn)解。
但這還不是他最偉大的成就。
1941年,香農(nóng)去了貝爾實(shí)驗(yàn)室,在那里他從事戰(zhàn)爭(zhēng)事務(wù),包括密碼學(xué)。他還研究信息和通信背后的原始理論。1948年,貝爾實(shí)驗(yàn)室研究期刊發(fā)表了他的研究,也就是劃時(shí)代的題為“通信的一個(gè)數(shù)學(xué)理論”論文。
香農(nóng)將信息源產(chǎn)生的信息量(例如,信息中的信息量)通過(guò)一個(gè)類似于物理學(xué)中熱力學(xué)熵的公式得到。用最基本的術(shù)語(yǔ)來(lái)說(shuō),香農(nóng)的信息熵就是編碼信息所需的二進(jìn)制數(shù)字的數(shù)量。對(duì)于概率為p的信息或事件,它的最特殊(即最緊湊)編碼將需要-log2(p)比特。
而這正是在貝葉斯定理中的最大后驗(yàn)表達(dá)式中出現(xiàn)的那些術(shù)語(yǔ)的本質(zhì)!
因此,我們可以說(shuō),在貝葉斯推理的世界中,最可能的假設(shè)取決于兩個(gè)術(shù)語(yǔ),它們引起長(zhǎng)度感(sense of length),而不是最小長(zhǎng)度。

那么長(zhǎng)度的概念是什么呢?
Length (h): 奧卡姆剃刀
奧卡姆的威廉(William of Ockham,約1287-1347)是一位英國(guó)圣方濟(jì)會(huì)修士和神學(xué)家,也是一位有影響力的中世紀(jì)哲學(xué)家。他作為一個(gè)偉大的邏輯學(xué)家而享有盛名,名聲來(lái)自他的被稱為奧卡姆剃刀的格言。剃刀一詞指的是通過(guò)“剔除”不必要的假設(shè)或分割兩個(gè)相似的結(jié)論來(lái)區(qū)分兩個(gè)假設(shè)。
奧卡姆剃刀的原文是“如無(wú)必要勿增實(shí)體”。用統(tǒng)計(jì)學(xué)的話說(shuō),我們必須努力用最簡(jiǎn)單的假設(shè)來(lái)解釋所有數(shù)據(jù)。
其他杰出人物響應(yīng)了類似的原則。
牛頓說(shuō):“解釋自然界的一切,應(yīng)該追求使用最少的原理。”
羅素說(shuō):“只要有可能,用已知實(shí)體的結(jié)構(gòu)去替代未知實(shí)體的推論。”
人們總是喜歡更短的假設(shè)。
那么我們需要一個(gè)關(guān)于假設(shè)的長(zhǎng)度的例子嗎?
下面哪個(gè)決策樹(shù)的長(zhǎng)度更小?A還是B?
即使沒(méi)有一個(gè)對(duì)假設(shè)的“長(zhǎng)度”的精確定義,我相信你肯定會(huì)認(rèn)為左邊的樹(shù)(A)看起來(lái)更小或更短。當(dāng)然,你是對(duì)的。因此,更短的假設(shè)就是,它要么自由參數(shù)更少,要么決策邊界更不復(fù)雜,或者這些屬性的某種組合可以表示它的簡(jiǎn)潔性。
那么Length(D | h)是什么?
給定假設(shè)是數(shù)據(jù)的長(zhǎng)度。這是什么意思?
直觀地說(shuō),它與假設(shè)的正確性或表示能力有關(guān)。給定一個(gè)假設(shè),它支配著數(shù)據(jù)的“推斷”能力。如果假設(shè)很好地生成了數(shù)據(jù),并且我們可以無(wú)錯(cuò)誤地測(cè)量數(shù)據(jù),那么我們就根本不需要數(shù)據(jù)。
想想牛頓的運(yùn)動(dòng)定律。
牛頓運(yùn)動(dòng)定律第一次出現(xiàn)在《自然哲學(xué)的數(shù)學(xué)原理》上時(shí),它們并沒(méi)有任何嚴(yán)格的數(shù)學(xué)證明。它們不是定理。它們很像基于對(duì)自然物體運(yùn)動(dòng)的觀察而做出的假設(shè)。但是它們對(duì)數(shù)據(jù)的描述非常好。因此它們就變成了物理定律。
這就是為什么你不需要記住所有可能的加速度數(shù)字,你只需要相信一個(gè)簡(jiǎn)潔的假設(shè),即F=ma,并相信所有你需要的數(shù)字都可以在必要時(shí)從這個(gè)假設(shè)中計(jì)算出來(lái)。它使得Length(D | h) 非常小。
但是如果數(shù)據(jù)與假設(shè)有很大的偏差,那么你需要對(duì)這些偏差是什么,它們可能的解釋是什么等進(jìn)行詳細(xì)描述。
因此,Length(D | h)簡(jiǎn)潔地表達(dá)了“數(shù)據(jù)與給定假設(shè)的匹配程度”這個(gè)概念。
實(shí)質(zhì)上,它是錯(cuò)誤分類(misclassication)或錯(cuò)誤率( error rate)的概念。對(duì)于一個(gè)完美的假設(shè),它是很短的,在極限情況下它為零。對(duì)于一個(gè)不能完美匹配數(shù)據(jù)的假設(shè),它往往很長(zhǎng)。
而且,存在著權(quán)衡。
如果你用奧卡姆剃刀刮掉你的假設(shè),你很可能會(huì)得到一個(gè)簡(jiǎn)單的模型,一個(gè)無(wú)法獲得所有數(shù)據(jù)的模型。因此,你必須提供更多的數(shù)據(jù)以獲得更好的一致性。另一方面,如果你創(chuàng)建了一個(gè)復(fù)雜的(長(zhǎng)的)假設(shè),你可能可以很好地處理你的訓(xùn)練數(shù)據(jù),但這實(shí)際上可能不是正確的假設(shè),因?yàn)樗`背了MAP 原則,即假設(shè)熵是小的。
將所有這些結(jié)合起來(lái)
因此,貝葉斯推理告訴我們,最好的假設(shè)就是最小化兩個(gè)項(xiàng)之和:假設(shè)的長(zhǎng)度和錯(cuò)誤率。
這句話幾乎涵蓋了所有(有監(jiān)督)機(jī)器學(xué)習(xí)。
想想它的結(jié)果:
線性模型的模型復(fù)雜度——選擇多項(xiàng)式的程度,如何減少平方和殘差。
神經(jīng)網(wǎng)絡(luò)架構(gòu)的選擇——如何不公開(kāi)訓(xùn)練數(shù)據(jù),達(dá)到良好的驗(yàn)證精度,并且減少分類錯(cuò)誤。
支持向量機(jī)正則化和kernel選擇——軟邊界與硬邊界之間的平衡,即用決策邊界非線性來(lái)平衡精度
我們真正得出的結(jié)論是什么?
我們從最小描述長(zhǎng)度(MDL)原理的分析中得出什么結(jié)論?
這是否一勞永逸地證明了短的假設(shè)就是最好的?
沒(méi)有。
MDL表明,如果選擇假設(shè)的表示(representation)使得h的大小為-log2 P(h),并且如果異常(錯(cuò)誤)的表示被選擇,那么給定h的D的編碼長(zhǎng)度等于-log2 P(D | h),然后MDL原則產(chǎn)生MAP假設(shè)。
然而,為了表明我們有這樣一個(gè)表示,我們必須知道所有先驗(yàn)概率P(h),以及P(D | h)。沒(méi)有理由相信MDL假設(shè)相對(duì)于假設(shè)和錯(cuò)誤/錯(cuò)誤分類的任意編碼應(yīng)該是首選。
對(duì)于實(shí)際的機(jī)器學(xué)習(xí),人類設(shè)計(jì)者有時(shí)可能更容易指定一種表示來(lái)獲取關(guān)于假設(shè)的相對(duì)概率的知識(shí),而不是完全指定每個(gè)假設(shè)的概率。
這就是知識(shí)表示和領(lǐng)域?qū)I(yè)知識(shí)變得無(wú)比重要的地方。它使(通常)無(wú)限大的假設(shè)空間變小,并引導(dǎo)我們走向一組高度可能的假設(shè),我們可以對(duì)其進(jìn)行最優(yōu)編碼,并努力找到其中的一組MAP假設(shè)。
總結(jié)和思考
一個(gè)奇妙的事實(shí)是,如此簡(jiǎn)單的一套數(shù)學(xué)操作就能在概率論的基本特征之上產(chǎn)生對(duì)監(jiān)督機(jī)器學(xué)習(xí)的基本限制和目標(biāo)的如此深刻而簡(jiǎn)潔的描述。對(duì)這些問(wèn)題的簡(jiǎn)明闡述,讀者可以參考來(lái)自CMU的一篇博士論文《機(jī)器學(xué)習(xí)為何有效》(Why Machine Learning Works)。
-
機(jī)器學(xué)習(xí)
+關(guān)注
關(guān)注
66文章
8490瀏覽量
134043 -
數(shù)據(jù)科學(xué)
+關(guān)注
關(guān)注
0文章
168瀏覽量
10394
原文標(biāo)題:當(dāng)貝葉斯,奧卡姆和香農(nóng)一起來(lái)定義機(jī)器學(xué)習(xí)
文章出處:【微信號(hào):AI_era,微信公眾號(hào):新智元】歡迎添加關(guān)注!文章轉(zhuǎn)載請(qǐng)注明出處。
發(fā)布評(píng)論請(qǐng)先 登錄
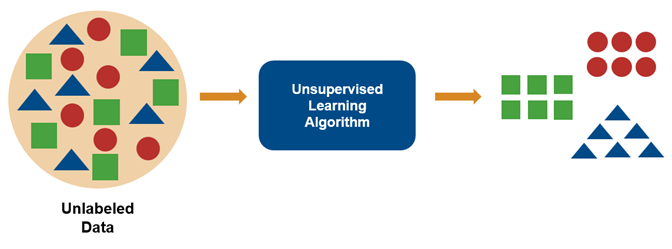
使用MATLAB進(jìn)行無(wú)監(jiān)督學(xué)習(xí)
機(jī)器學(xué)習(xí)技術(shù)在圖像分類和目標(biāo)檢測(cè)上的應(yīng)用
【下載】《機(jī)器學(xué)習(xí)》+《機(jī)器學(xué)習(xí)實(shí)戰(zhàn)》
【阿里云大學(xué)免費(fèi)精品課】機(jī)器學(xué)習(xí)入門:概念原理及常用算法
如何用卷積神經(jīng)網(wǎng)絡(luò)方法去解決機(jī)器監(jiān)督學(xué)習(xí)下面的分類問(wèn)題?
如何使用深度學(xué)習(xí)進(jìn)行視頻行人目標(biāo)檢測(cè)
你想要的機(jī)器學(xué)習(xí)課程筆記在這:主要討論監(jiān)督學(xué)習(xí)和無(wú)監(jiān)督學(xué)習(xí)
如何用Python進(jìn)行無(wú)監(jiān)督學(xué)習(xí)
無(wú)監(jiān)督機(jī)器學(xué)習(xí)如何保護(hù)金融
機(jī)器學(xué)習(xí)算法中有監(jiān)督和無(wú)監(jiān)督學(xué)習(xí)的區(qū)別
最基礎(chǔ)的半監(jiān)督學(xué)習(xí)
半監(jiān)督學(xué)習(xí)最基礎(chǔ)的3個(gè)概念
為什么半監(jiān)督學(xué)習(xí)是機(jī)器學(xué)習(xí)的未來(lái)?
機(jī)器學(xué)習(xí)中若干典型的目標(biāo)函數(shù)構(gòu)造方法
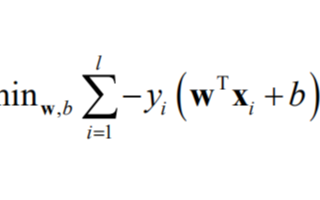
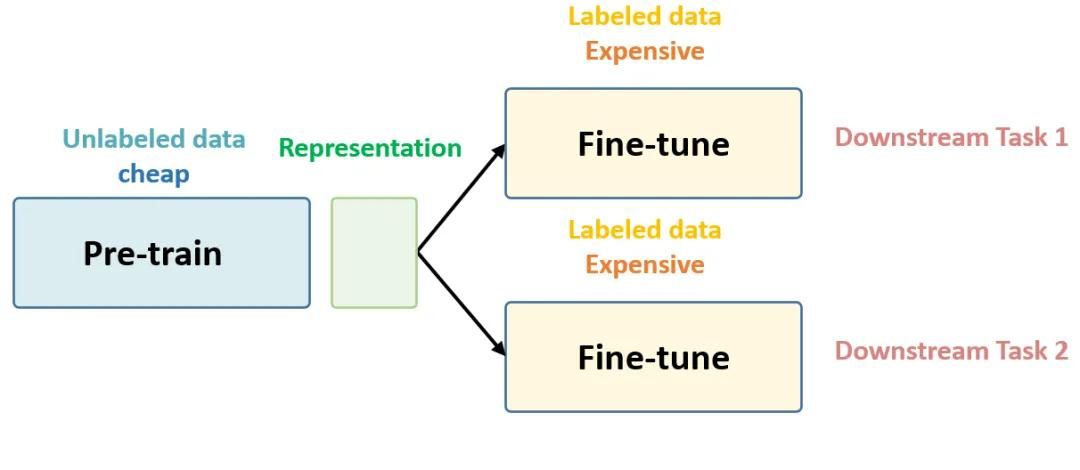
機(jī)器學(xué)習(xí)中的無(wú)監(jiān)督學(xué)習(xí)應(yīng)用在哪些領(lǐng)域





 對(duì)監(jiān)督機(jī)器學(xué)習(xí)的基本限制和目標(biāo)進(jìn)行深刻而簡(jiǎn)潔的描述
對(duì)監(jiān)督機(jī)器學(xué)習(xí)的基本限制和目標(biāo)進(jìn)行深刻而簡(jiǎn)潔的描述










評(píng)論