摘要:
光學測量領域中,光源對恒流源的要求較高,現有的恒流源系統存在著系統噪聲與測量噪聲,影響了電流的輸出精度。將Kalman濾波算法與FOPID控制策略相結合,構建Kalman-FOPID控制器,在以BUCK電路為核心的流控型恒流源系統數學模型的基礎上,利用MATLAB產生隨機噪聲,進行電流控制研究。仿真及實物驗證表明,Kalman-FOPID控制器可以有效濾除恒流源系統的噪聲干擾,提高輸出電流的控制精度。
0 引言
恒流源是輸出穩定電流以驅動負載工作的電源,常應用在半導體光源[1]、物性型敏感器件[2]、充電裝置[3]等領域中,而恒流源輸出電流的好壞,直接影響光學測量精度和應用對象使用壽命。因此,對恒流源的研究存在積極的現實意義。在對恒流源系統的研究中,文獻[4]采用雙級恒流源硬件電路,用以降低電流噪聲的干擾,并應用于固態激光器;文獻[5]通過諧振開關反饋控制MOS管,以解決負載的過流問題。上述對恒流源的研究,注重通過電路設計解決電流控制過程中產生的問題,但忽略了非理想狀態下系統噪聲和測量噪聲的存在,以至于影響了恒流源系統的電流輸出效果。
Kalman濾波算法可以有效解決控制過程中由噪聲干擾引起的誤差[6],分數階PID(Fractional Order Proportional Integral Differential,FOPID)在溫度系統[7]、生物反應器[8]等應用中控制效果顯著。為改善恒流源的輸出效果,本文提出將Kalman濾波算法與FOPID控制策略相結合,構建Kalman-FOPID控制器,并對恒流源電路進行數學建模,在利用MATLAB對Kalman-FOPID控制器的控制效果驗證的基礎上,進行硬件測試。實驗結果表明,Kalman-FOPID控制器能夠有效濾除系統中的噪聲干擾,提高電流的輸出精度,使系統穩定可靠。
1 恒流源系統與數學建模
1.1 恒流源系統結構
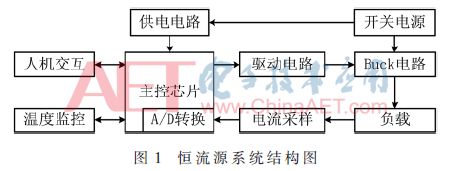
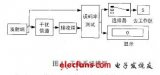
恒流源系統結構如圖1所示,用戶輸入設定電流值,主控芯片根據設定值輸出占空比為D的PWM波,經驅動電路控制BUCK電路中MOS管通斷,以調整加在負載兩端的電壓,而流過負載的電流值經電流采樣、A/D轉換為數字量后送入主控芯片內,主控芯片根據電流設定值與實際值的偏差調整PWM的占空比,以實現流過負載電流的穩定。
1.2 恒流源系統的數學模型
本文恒流源電路是基于BUCK電路來實現的,通過控制MOS管的通斷改變負載兩端的電壓,以使流過負載的電流保持恒定,在忽略電感電阻和電容電阻條件下,電路原理圖如圖2所示。
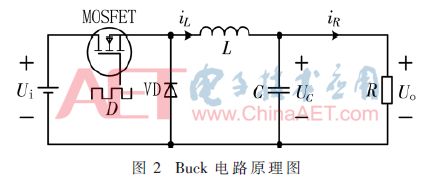
設恒流源的輸入電壓為Ui,驅動MOSFET的PWM波占空比為D,周期為T,電感電流為iL,電容電壓為UC,負載R兩端電壓為UO,流過負載電流為iR。通過增大電感L,使BUCK電路工作在連續工作模式下。在任意t∈[ti-1,ti]時刻,i=1,2,3…,有:
(1)在t∈[ti-1,DT+ti-1]時,PWM波為高電平,驅動MOS管導通,此時電路的狀態空間方程為:

2 Kalman-FOPID控制器設計
2.1 FOPID控制算法
FOPID的頻域形式為:
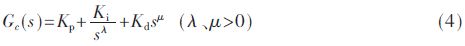
式中Kp、Ki、Kd為比例、積分、微分系數,λ、μ分別是積分、微分的階數。IOPID是FOPID在λ=1、μ=1的特殊情況,有固定的整定方法,實現簡單,但只有3個可調參數;FOPID有5個可調參數,雖然整定方法復雜,但參數設置靈活,控制效果較好,且魯棒性強。FOPID在時域的形式為:

2.2 Kalman-FOPID控制器
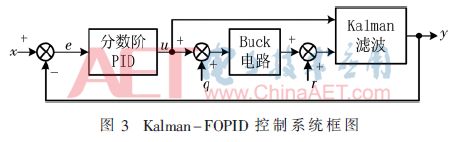
Kalman-FOPID控制系統框圖如圖3所示。將電流設定值x與實際值y的偏差e送入FOPID控制器中,輸出u在受系統噪聲q的干擾后驅動BUCK電路中MOS管通斷,使負載工作;對負載電流采樣時,采樣值與實際值之間存在測量噪聲r,利用Kalman濾波算法降低噪聲q和r的影響,使電流實際值y準確反饋到控制器,以實現閉環控制。
Kalman-FOPID控制算法流程:
(1)對恒流源系統的傳遞函數進行z變換,得到離散型線性系統時域形式:

(4)根據設定值與觀測值的誤差e采用FOPID控制算法調整輸出zk;
(5)測量更新:
計算Kalman增益Kk:
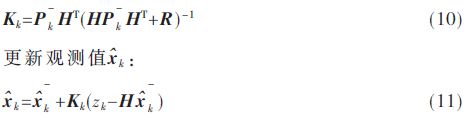
更新誤差協方差Pk:

(6)重復步驟(3)到步驟(5),進行下一次Kalman-FOPID控制,直到輸出電流滿足系統要求。
3 實驗分析
為了探究 Kalman-FOPID控制器對存在系統噪聲和測量噪聲干擾的恒流源系統的控制效果,采用MATLAB軟件依次使用IOPID、FOPID、Kalman-IOPID、Kalman-FOPID 4種控制策略進行仿真,比較4種控制策略之間的控制效果,并利用硬件驗證Kalman-FOPID應用在恒流源系統的可行性和控制效果。
3.1 仿真研究
根據恒流源系統的數學模型,設計參數為:Ui=12 V,L=2 H,C=4 400 μF,R=10 Ω,Ts=0.000 1 s,仿真時間為1 s。此時系統的流控型傳遞函數為:

恒流源系統中存在的系統噪聲與測量噪聲,是利用MATLAB的隨機函數rand()產生的,幅值為0.000 2。Kalman濾波算法中的參數初始化為:Q=1、R=1;各控制器的參數采用粒子群算法尋優并結合試驗法得出最優值,具體如表1所示。
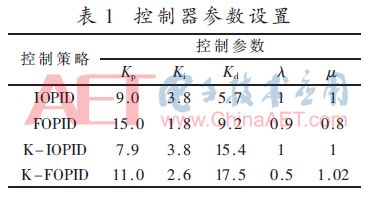
當控制系統輸入為階躍響應,幅值為1 A時,4種控制策略響應曲線及特性如下:
(1)IOPID與FOPID響應曲線
IOPID與FOPID在響應過程中受隨機噪聲的干擾,每次仿真的結果各不相同,圖4是仿真結果之一,為了比較IOPID和FOPID的控制效果,連續仿真50次,統計各自最大超調量偏差、0.1 s后響應過程的最大波動誤差,統計結果如圖5所示。
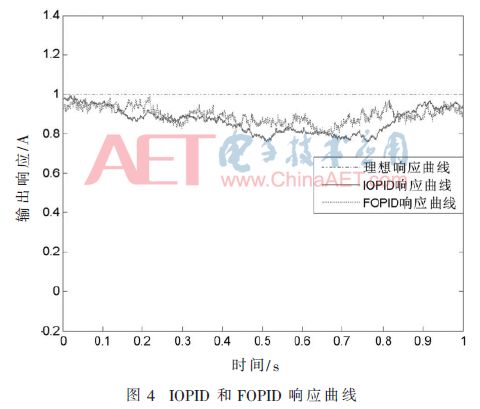
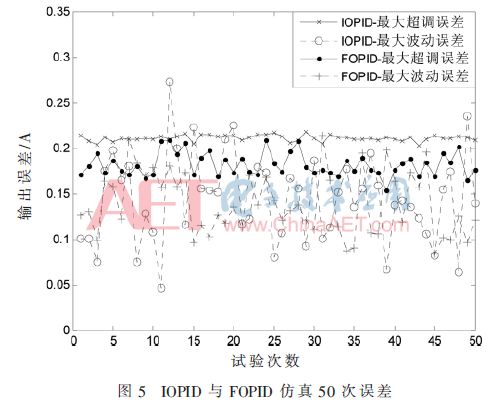
在多次仿真過程中,IOPID響應曲線在0.000 5 s達到最大超調量,且超調量比較穩定;FOPID響應曲線在0.001 2 s達到最大超調量,超調量波動較大,但總體小于IOPID的最大超調量;IOPID與FOPID在響應時間0.1 s后的最大波動誤差變化都比較大。因此,IOPID與FOPID在有噪聲干擾的恒流源系統中控制效果較差。
(2)Kalman-IOPID與Kalman-FOPID響應曲線
Kalman-IOPID與Kalman-FOPID中Kalman濾波算法可以有效降低隨機噪聲的干擾,多次仿真的結果相同,響應曲線如圖6所示。
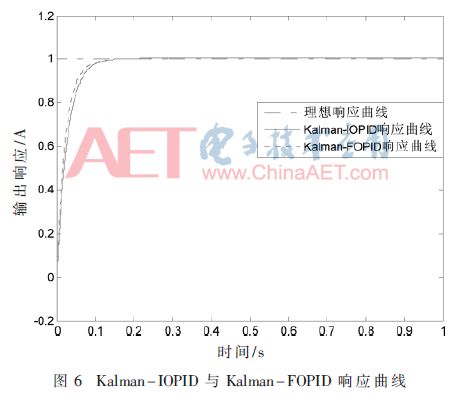
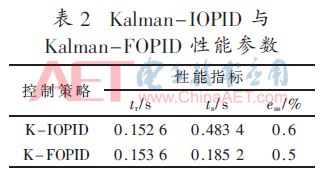
根據圖6仿真曲線,控制策略的上升時間tr、穩態時間ts、穩態誤差ess的參數如表2所示。與Kalman-IOPID相比,Kalman-FOPID上升時間tr較長,但從響應到穩態的時間為0.338 8 s,小于Kalman-IOPID的0.636 0 s,并且穩態誤差也較小。因此,Kalman-IOPID與Kalman-FOPID可以有效控制存在噪聲的恒流源系統,其中Kalman-FOPID從響應到穩態的時間短,穩態誤差小。
通過采用MATLAB進行仿真研究可知,Kalman濾波算法可以降低隨機噪聲對系統的影響,將Kalman濾波算法與FOPID控制策略相結合的Kalman-FOPID控制器理論上可以控制存在噪聲干擾的流控型恒流源系統,并取得較好控制的效果。
3.2 硬件測試
為進一步驗證Kalman-FOPID算法控制效果,根據圖1設計恒流源電路,采用Kalman-FOPID控制算法,硬件測試過程如下:
(1)當設定電流較小時,為了降低采樣電阻的影響,選擇較大的負載電阻。選取阻值為16.8 Ω,依次設定電流值,測量數據如表3所示。
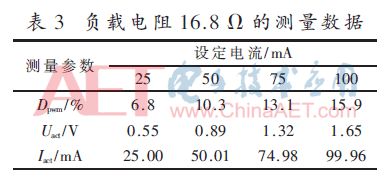
(2)當設定電流較大時,為使系統輸出較大電流,負載電阻應當較小。調整負載電阻為8.2 Ω時,不同設定電流值的測量數據如表4所示。
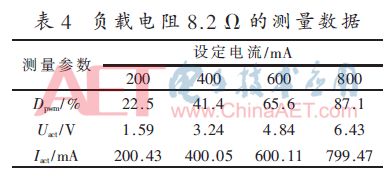
由測量數據可知,在小電流控制時,負載電阻為16.8 Ω時最大電流誤差為0.04 mA;在大電流輸出時,負載電阻為8.2 Ω時最大電流誤差為0.53 mA。電流的設定值與實際值誤差較小,表明Kalman-FOPID控制策略可應用于恒流源系統中,并且有效降低系統中噪聲干擾,輸出電流穩定、控制精度高。
4 結論
本文針對恒流源系統中存在的系統噪聲和測量噪聲的干擾問題,提出了將Kalman濾波算法和FOPID控制策略相結合,構建Kalman-FOPID控制器,在建立以BUCK電路為核心的流控型恒流源系統數學模型的基礎上,合理設置參數,利用MATLAB模擬噪聲干擾,進行恒流源的控制仿真。仿真結果表明Kalman-IOPID和Kalman-FOPID可以降低系統中噪聲的干擾,輸出電流的控制性能參數較好,其中Kalman-FOPID到達穩態的時間較短、穩態誤差較小。通過搭建恒流源硬件控制系統實驗電路,通過調整負載情況,觀察測量電流輸出,實驗結果表明電流穩定性好、控制精度高,能夠應用于對電流輸出要求高的工業場所,尤其是對電流變化敏感的半導體光源,對其亮度質量的控制和使用壽命的延長起到促進作用。
-
噪聲
+關注
關注
13文章
1137瀏覽量
47889 -
恒流源
+關注
關注
16文章
340瀏覽量
56796 -
Kalman
+關注
關注
0文章
11瀏覽量
8282
原文標題:【學術論文】Kalman-FOPID算法在數控恒流源中的控制研究
文章出處:【微信號:ChinaAET,微信公眾號:電子技術應用ChinaAET】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
白光LED通信系統的噪聲與干擾分析
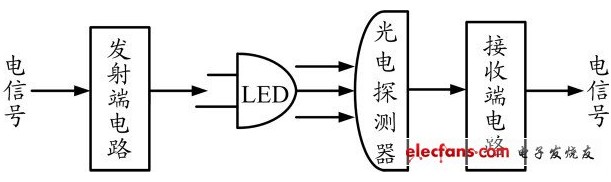
工業測量中的噪聲干擾問題
如何處理DSP系統中的噪聲和電磁干擾EMI
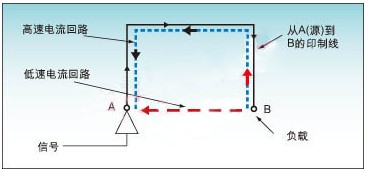
DSP系統中噪聲和電磁干擾EMI的影響以及控制方法
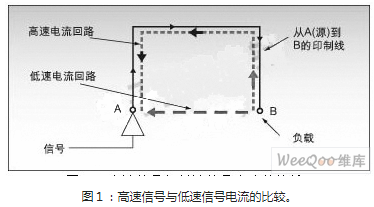





 針對恒流源系統中存在的系統噪聲和測量噪聲的干擾問題
針對恒流源系統中存在的系統噪聲和測量噪聲的干擾問題










評論