一. FOC之使用Cordic算法求解sin/cos

在進(jìn)行坐標(biāo)變換的時(shí)候，需要計(jì)算角度的正余弦值，而在FPGA中是不能直接進(jìn)行求解的，需要采用其它的方式進(jìn)行求解。最常使用的方法有如下兩種:

基于ROM的查找表方式: 首先在PC上使用python等高級(jí)語言將一個(gè)周期內(nèi)的正余弦值全部計(jì)算出來，角度的分辨率根據(jù)實(shí)際需求來確定，分辨率越精細(xì)，那么需要存儲(chǔ)ROM的深度就越深，反之約小，然后將計(jì)算出來的正余弦值進(jìn)行一個(gè)擴(kuò)大取整保留數(shù)據(jù)精度，最后按照角度順序依次存入ROM中。很明顯，通過這種方式計(jì)算正余弦值所需要的時(shí)鐘周期特別短，消耗FPGA的存儲(chǔ)資源大。

基于Cordic算法計(jì)算: Cordic算法并不直接求解正余弦值，而且通過旋轉(zhuǎn)逼近的思想來進(jìn)行擬合正余弦函數(shù)。該算法擬合的精度非常高，因而被廣泛應(yīng)用于計(jì)算機(jī)圖形學(xué)、數(shù)字信號(hào)處理等領(lǐng)域。

Cordic算法運(yùn)算過程中，只設(shè)計(jì)到移位和加減運(yùn)算，這種運(yùn)算是非常適合于FPGA的，從面積和計(jì)算速度兩方面進(jìn)行綜合考慮，最終選擇占用面積較小、計(jì)算速度略低的Cordic算法來求解sin/cos函數(shù)值。

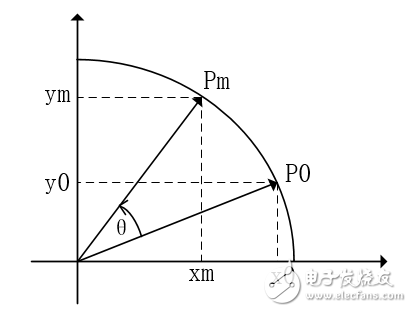
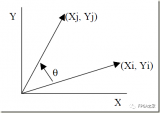
首先如下圖所示，假設(shè)單位圓上有任意兩點(diǎn)Q和P，它們之間的角度關(guān)系已知，則它們的XY軸坐標(biāo)可以表示如下:

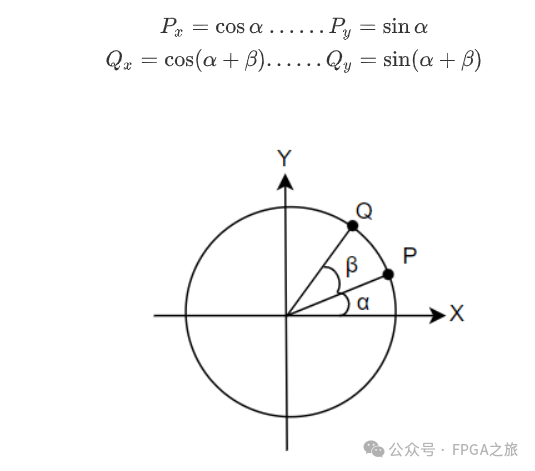
將Q點(diǎn)的坐標(biāo)公式進(jìn)行展開，然后再將P點(diǎn)的坐標(biāo)公式代入其中可得:

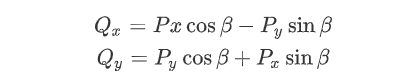
為了統(tǒng)一變量類型，將cos函數(shù)作為公共相提取出來，可以得到如下形式:

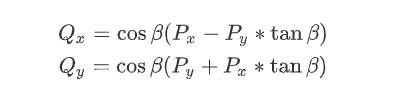
可以看出，由P點(diǎn)旋轉(zhuǎn)至Q點(diǎn)后，Q點(diǎn)的最終表達(dá)式如上所示，這種形式便是Cordic算法旋轉(zhuǎn)的基本公式了。如果將旋轉(zhuǎn)初始點(diǎn)P設(shè)置為一個(gè)特殊位置：X軸上，那么很明顯Q點(diǎn)的坐標(biāo)值就是對(duì)應(yīng)旋轉(zhuǎn)角度的正余弦值。

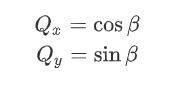
有了上述基本推論，就可以開始真正的進(jìn)行旋轉(zhuǎn)擬合了。P點(diǎn)直接一步旋轉(zhuǎn)到Q點(diǎn)，肯定是不可取的。如果將P點(diǎn)經(jīng)過多次旋轉(zhuǎn)，每一次旋轉(zhuǎn)的角度均為特殊角度,tan函數(shù)對(duì)應(yīng)的角度值如下，這樣就將乘法運(yùn)算巧妙的轉(zhuǎn)換成了左移運(yùn)算。

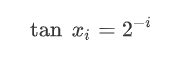
每一次旋轉(zhuǎn)迭代的公式如下，每一次旋轉(zhuǎn)的公式里面還包括了cos函數(shù)，這也是不方便在FPGA內(nèi)計(jì)算的，觀察表達(dá)式可以知道，cos函數(shù)在這里起到的作用是對(duì)坐標(biāo)值起到等比例縮放的作用，并不會(huì)影響旋轉(zhuǎn)的點(diǎn)對(duì)應(yīng)向量的方向。

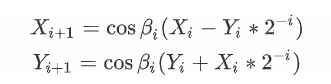
所以可以將每一次旋轉(zhuǎn)過程中的cos函數(shù)提取出來，最后進(jìn)行運(yùn)算，這樣就不用參與到每次的旋轉(zhuǎn)計(jì)算中去，由于旋轉(zhuǎn)的角度是已知的，所以當(dāng)確定好旋轉(zhuǎn)次數(shù)后，可以將這部分運(yùn)算提取計(jì)算出來，作為一個(gè)系數(shù)K，K的表達(dá)式如下圖所示。

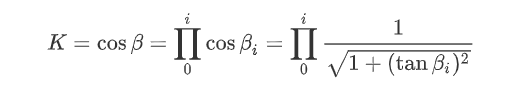
接下來就是需要研究每次旋轉(zhuǎn)對(duì)應(yīng)的角度值了，角度對(duì)應(yīng)的tan函數(shù)值是已知的，可以通過Python直接求解出對(duì)應(yīng)的角度，然后匯總成如下表格:

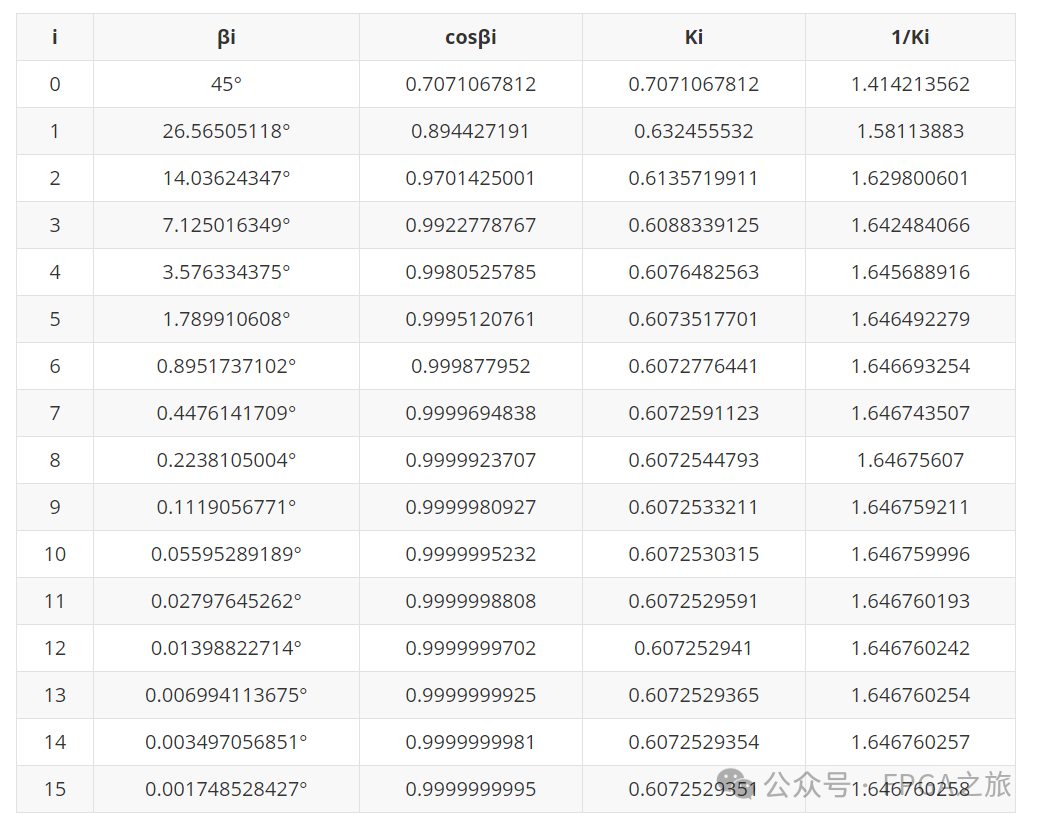
通過上表可以看出，當(dāng)旋轉(zhuǎn)到16次的時(shí)候，角度的誤差只有千分之一了，而cosβ和K的值均趨近于一個(gè)定值，故Cordic旋轉(zhuǎn)擬合是收斂的。在旋轉(zhuǎn)的過程中，可能會(huì)出現(xiàn)旋轉(zhuǎn)角度大于目標(biāo)角度的情況，所以在旋轉(zhuǎn)的過程中還需要增加一個(gè)變量d來控制旋轉(zhuǎn)的方向，另外用z來表示旋轉(zhuǎn)到的角度值，最終的旋轉(zhuǎn)迭代公式如下:

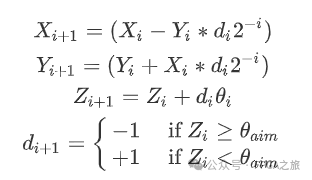
最終目標(biāo)角度的正余弦值如下:

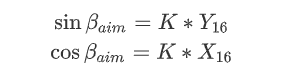
FPGA內(nèi)部實(shí)現(xiàn)的過程中，需要對(duì)旋轉(zhuǎn)角度值以及K值擴(kuò)大2^16次方，然后取整，為的是在保持計(jì)算精度的情況下，免去數(shù)據(jù)的小數(shù)部分，這些都是固定值，不會(huì)根據(jù)目標(biāo)角度的變化而變化，可以在程序中直接定義出來，如下圖所示。

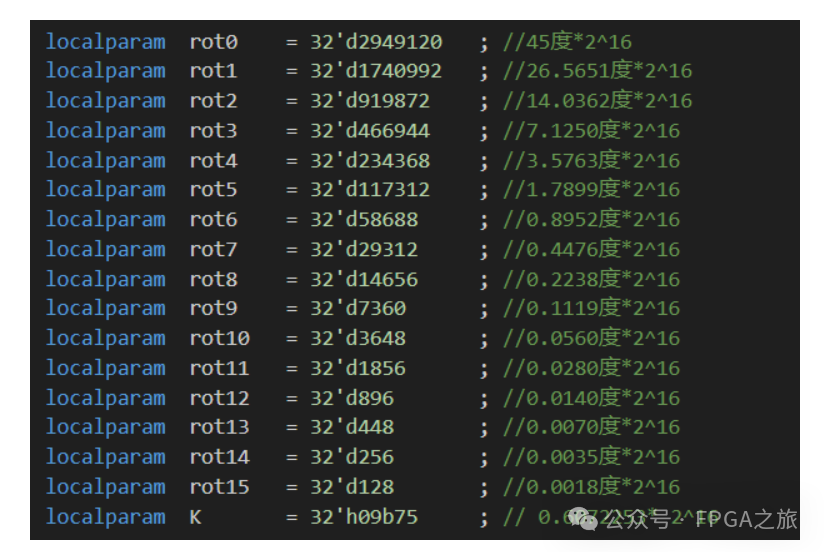
另外還要一個(gè)關(guān)鍵點(diǎn)需要注意的是迭代公式中使用的是tan函數(shù)，需要對(duì)目標(biāo)角度限制在-90°到90°范圍內(nèi)，所以在目標(biāo)角度輸入模塊之后，需要先對(duì)角度進(jìn)行一個(gè)象限變換，為了處理的方便，本設(shè)計(jì)將目標(biāo)角度變換到第一象限內(nèi)，也就是0°到90°，如下圖所示，象限變換不會(huì)影響正余弦數(shù)組的大小，只會(huì)影響其數(shù)值的符號(hào)，所以在迭代完成后，根據(jù)需要對(duì)坐標(biāo)點(diǎn)進(jìn)行取反運(yùn)行即可。

來源：本文轉(zhuǎn)載FPGA 之旅公眾號(hào)