最優化是指由變量x構成的目標函數f(x)進行最小化或最大化的過程。在機器學習或深度學習術語中,通常指最小化損失函數J(w),其中模型參數w∈R^d。最小化最優化算法具有以下的目標:
- 如果目標函數是凸的,那么任何的局部最小值都是全局最小值。
- 通常情況下,在大多數深度學習問題中,目標函數是非凸的,那就只能找到目標函數鄰域內的最低值。
圖1: 向著最小化邁進
目前主要有三種最優化算法:
- 對單點問題,最優化算法不用進行迭代和簡單求解。
- 對于邏輯回歸中經常用到梯度下降法,這類最優化算法本質上是迭代,不管參數初始化好壞都能收斂到可接受的解。
- 對于一系列具有非凸損失函數的問題中,如神經網絡。為保證收斂速度與低錯誤率,最優化算法中的參數初始化中起著至關重要的作用。
梯度下降是機器學習和深度學習中最常用的優化算法。它屬于一階優化算法,參數更新時只考慮一階導數。在每次迭代中,梯度表示最陡的上升方向,于是我們朝著目標函數梯度的反方向更新參數,并通過學習速率α來調整每次迭代中達到局部最小值的步長。因此,目標函數會沿著下坡的方向,直到達到局部最小值。
在本文中,我們將介紹梯度下降算法及其變種:批量梯度下降,小批量梯度下降和隨機梯度下降。
我們先看看梯度下降是如何在邏輯回歸中發揮作用的,然后再討論其它變種算法。簡單起見,我們假設邏輯回歸模型只有兩個參數:權重w和偏差b。
1.將初始化權重w和偏差b設為任意隨機數。
2.為學習率α選擇一個合適的值,學習速率決定了每次迭代的步長。
- 如果α非常小,則需要很長時間才能收斂并且計算量很大。
- 如果α較大,則可能無法收斂甚至超出最小值。
- 通過我們會使用以下值作為學習速度 : 0.001, 0.003, 0.01, 0.03, 0.1, 0.3.

圖2: 不同學習速度下的梯度下降
因此,通過觀察比較不同的α值對應的損失函數變化,我們選擇第一次未達到收斂的α值的前一個作為最終的α值,這樣我們就可以有一個快速且收斂的學習算法。
3.如果數據尺度不一,那就要對數據進行尺度縮放。如果我們不縮放數據,那么等高線(輪廓)會變得越來越窄,意味著它需要更長的時間來達到收斂(見圖3)。

圖3. 梯度下降: 數據歸一化后的等高線與未進行歸一化的對比
使數據分布滿足μ= 0和σ= 1。以下是數據縮放的公式:

4.在每次迭代中,用損失函數J的偏導數來表示每個參數(梯度)

更新方程如下:

- 特地說明一下,此處我們假設不存在偏差。 如果當前值w對應的梯度方向為正,這意味著當前點處在最優值w*的右側,則需要朝著負方向更新,從而接近最優值w*。然而如果現在梯度是負值,那么更新方向將是正的,將增加w的當前值以收斂到w*的最優值(參見圖4):
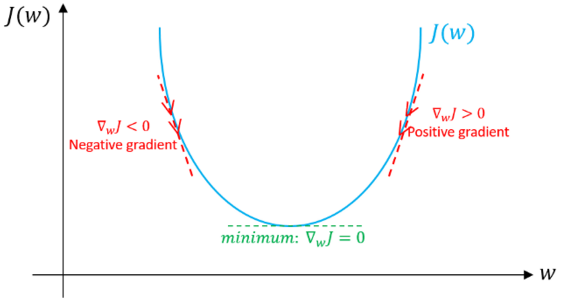
圖4: 梯度下降,示例說明梯度下降算法如何用損失函數的一階導數實現下降并達到最小值。
- 繼續這個過程,直至損失函數收斂。也就是說,直到誤差曲線變得平坦不變。
- 此外,每次迭代中,朝著變化最大的方向進行,每一步都與等高線垂直。
上面就是梯度下降法的一般過程,我們需要確定目標函數、優化方法,并通過梯度來引導系統搜尋到最優值。
現在我們來討論梯度下降算法的三個變種,它們之間的主要區別在于每個學習步驟中計算梯度時使用的數據量,是對每個參數更新(學習步驟)時的梯度準確性與時間復雜度的折衷考慮。
批量梯度下降
批量梯度下降是指在對參數執行更新時,在每次迭代中使用所有的樣本。

for i in range(num_epochs):
grad = compute_gradient(data, params)
params = params — learning_rate * grad
主要的優點:
- 訓練期間,我們可以使用固定的學習率,而不用考慮學習率衰減的問題。
- 它具有朝向最小值的直線軌跡,并且如果損失函數是凸的,則保證理論上收斂到全局最小值,如果損失函數不是凸的,則收斂到局部最小值。
- 梯度是無偏估計的。樣本越多,標準誤差就越低。
主要的缺點:
- 盡管我們可以用向量的方式計算,但是可能仍然會很慢地遍歷所有樣本,特別是數據集很大的時候算法的耗時將成為嚴重的問題。
- 學習的每一步都要遍歷所有樣本,這里面一些樣本可能是多余的,并且對更新沒有多大貢獻。
小批量梯度下降
為了克服上述方法的缺點,人們提出了小批量梯度下降。在更新每一參數時,不用遍歷所有的樣本,而只使用一部分樣本來進行更新。 因此,每次只用小批量的b個樣本進行更新學習,其主要過程如下:

- 打亂訓練數據集以避免樣本預先存在順序結構。
- 根據批量的規模將訓練數據集分為b個小批量。如果訓練集大小不能被批量大小整除,則將剩余的部分單獨作為一個小批量。
for i in range(num_epochs):
np.random.shuffle(data)
for batch in radom_minibatches(data, batch_size=32):
grad = compute_gradient(batch, params)
params = params — learning_rate * grad
批量的大小我們可以調整,通常被選為2的冪次方,例如32,64,128,256,512等。其背后的原因是一些像GPU這樣的硬件也是以2的冪次方的批量大小來獲得更好的運行時間。
主要的優點:
- 比起批量梯度下降,速度更快,因為它少用了很多樣本。
- 隨機選擇樣本有助于避免對學習沒有多大貢獻冗余樣本或非常相似的樣本的干擾。
- 當批量的大小小于訓練集大小時,會增加學習過程中的噪聲,有助于改善泛化誤差。
- 盡管用更多的樣本可以獲得更低的估計標準誤差,但所帶來的計算負擔卻小于線性增長
主要缺點:
- 在每次迭代中,學習步驟可能會由于噪聲而來回移動。 因此它會在最小值區域周圍波動,但不收斂。
- 由于噪聲的原因,學習步驟會有更多的振蕩(見圖4),并且隨著我們越來越接近最小值,需要增加學習衰減來降低學習速率。

圖5: 梯度下降:批量與小批量的損失函數對比
對于大規模的訓練數據集,我們通常不需要超過2-10次就能遍歷所有的訓練樣本。 注意:當批量大小b等于訓練樣本數m時候,這種方法就相當于批量梯度下降。
隨機梯度下降
隨機梯度下降(SGD)只對樣本(xi,yi)執行參數更新,而不是遍歷所有樣本。因此,學習發生在每個樣本上,其具體過程如下:
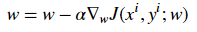
- 打亂訓練數據集以避免樣本預先存在順序
- 將訓練數據集劃分為m個樣本。
for i in range(num_epochs):
np.random.shuffle(data)
for example in data:
grad = compute_gradient(example, params)
params = params — learning_rate * grad
它與小批量版本擁有很多相似的優點和缺點。以下是特定于SGD的特性:
- 與小批量方法相比,它為學習過程增加了更多的噪聲,有助于改善泛化誤差。但同時也增加了運行時間。
- 我們不能用向量的形式來處理1個樣本,導致速度非常慢。 此外,由于每個學習步驟我們僅使用1個樣本,所以方差會變大。
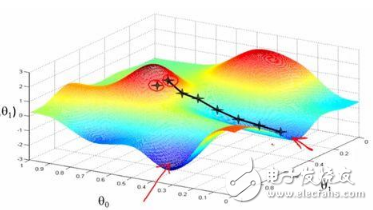
下圖顯示了梯度下降的變種方法以及它們朝向最小值的方向走勢,如圖所示,與小批量版本相比,SGD的方向噪聲很大:

圖6: 梯度下降變種方法朝向最小值的軌跡
難點
以下是關于梯度下降算法及其變種遇到的一些常見問題:
- 梯度下降屬于一階優化算法,這意味著它不考慮損失函數的二階導數。 但是,函數的曲率會影響每個學習步長的大小。梯度描述了曲線的陡度,二階導數則測量曲線的曲率。因此,如果:
1.二階導數= 0→曲率是線性的。 因此,步長=學習率α。
2.二階導數> 0→曲率向上。 因此,步長<學習率α可能會導致發散。
3.二階導數<0→曲率向下。 因此,步長>學習率α。
因此,對梯度看起來有希望的方向可能不會如此,并可能導致學習過程減慢甚至發散。
- 如果Hessian矩陣不夠好,比如最大曲率的方向要比最小曲率的方向曲率大得多。 這將導致損失函數在某些方向上非常敏感,而在其他方向不敏感。 因此,有些看起來有利于梯度的方向可能不會導致損失函數發生很大變化(請參見圖7)。

圖7: 梯度下降未能利用包含在Hessian矩陣中的曲率信息。
- 隨著每個學習步驟完成,梯度gTg的范數應該緩慢下降,因為曲線越來越平緩,曲線的陡度也會減小。 但是,由于曲線的曲率使得梯度的范數在增加。盡管如此,但我們還能夠獲得非常低的錯誤率(見圖8)。

圖8: 梯度范數. Source
- 在小規模數據集中,局部最小值是常見的; 然而,在大規模數據集中,鞍點更為常見。鞍點是指函數在某些方向上向上彎曲而在其他方向上向下彎曲。換句話說,鞍點看起來像是一個方向的最小值,另一個方向的最大值(見圖9)。 當Hessian矩陣的特征值至少有一個是負值而其余的特征值是正值時就會發生這種情況。

圖9: 鞍點
- 如前所述,選擇適當的學習率是困難的。 另外,對于小批量梯度下降,我們必須在訓練過程中調整學習速率,以確保它收斂到局部最小值而不是在其周圍來回游蕩。計算學習率的衰減率也是很難的,并且這會隨著數據集不同而變化。
- 所有參數更新具有相同的學習率; 然而,我們可能更希望對一些參數執行更大的更新,因為這些參數的方向導數比其他參數更接近朝向最小值的軌跡,那么就需要針對性的設定學習率及其變化。
-
機器學習
+關注
關注
66文章
8490瀏覽量
134062 -
深度學習
+關注
關注
73文章
5554瀏覽量
122467
原文標題:機器學習優化算法「梯度下降」及其變種算法
文章出處:【微信號:thejiangmen,微信公眾號:將門創投】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄





 梯度下降算法及其變種:批量梯度下降,小批量梯度下降和隨機梯度下降
梯度下降算法及其變種:批量梯度下降,小批量梯度下降和隨機梯度下降

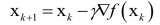











評論