“非常棒的分享，強烈推薦！想嘗試做自動布線工具的小伙伴都來學習下。本文來自 tscircuit 的主要作者 SEVE，詳細總結了耗費約一年時間嘗試打造全球最快自動布線工具的重要經驗。”

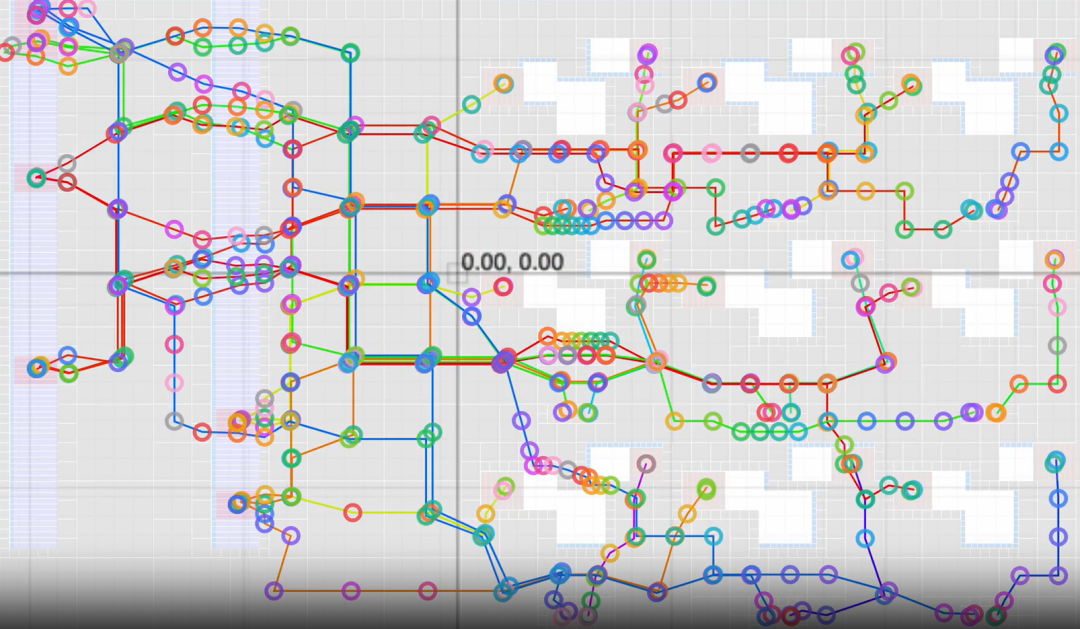
我在為 tscircuit（一款用TypeScript編寫的開源電子CAD內核）開發自動布線工具上耗費了約一年時間。如果我能回到一年前，以下是我會告訴自己的13件事：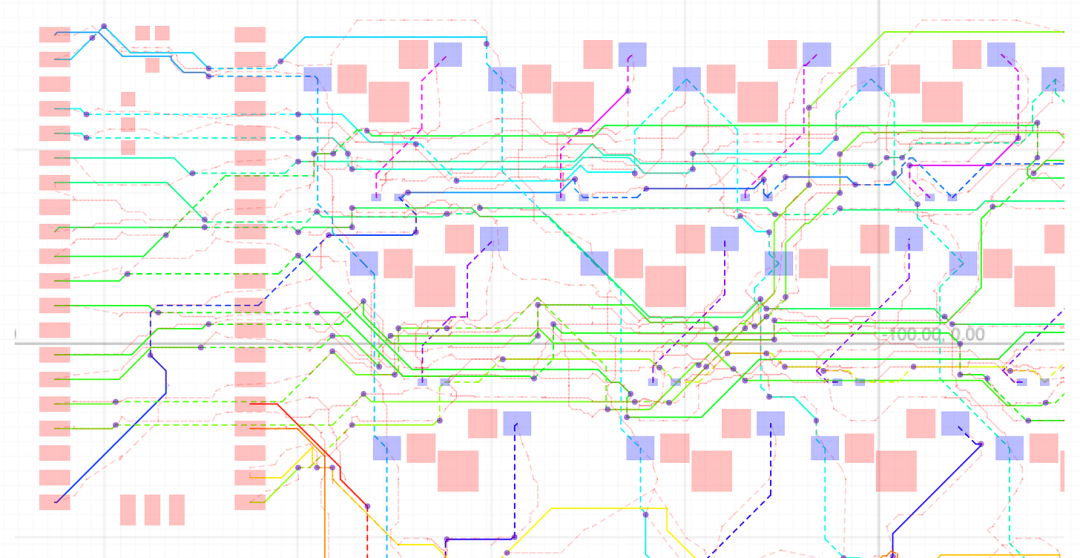

一個鍵盤項目自動布線的中間階段

1. 像熟悉自己的手掌一樣掌握 A* 算法

如果我能當一天國王，我會把 A*算法改名為"基礎算法"。這確實是任何類型搜索中最具適應性和重要性的算法之一。它簡直是為各種啟發式搜索（不局限于二維網格！）打造的最佳基礎框架。

這里展示的是二維網格中 A*算法與"廣度優先搜索"算法的動畫對比：

A*算法探索節點的方式要快速直觀得多。這兩種算法的主要區別在于，廣度優先搜索會探索所有相鄰節點，而 A*會優先探索距離目標更近的節點。由于它考慮了圖結構外的度量標準（與目標的距離），因此屬于啟發式搜索。

您的代碼中很可能已經在使用廣度優先搜索或深度優先搜索。遞歸算法本質上就是深度優先搜索。任何不排序候選節點/相鄰節點就直接遍歷的循環結構都屬于廣度優先搜索。在99%的情況下，您都可以將其轉換為 A* 算法并獲得顯著的性能提升！

在我的自動布線器中，最讓我自豪的設計之一是通過運行多層 A*算法來發現特定場景的最優超參數。我們的做法本質上是將每個自動布線器作為候選方案運行，然后通過 A*算法確定哪些自動布線器最值得我們投入大量時間優化！

看到頂部那些數字了嗎？每個數字都代表不同的超參數配置。如果不加區分地運行每個自動布線器將造成巨大的時間浪費——當某個自動布線器開始勝出（即以較低成本成功布線）時，就應為它分配更多迭代次數！這種元A*(meta-A*) 算法將常規的路徑距離懲罰成本函數，與迭代次數懲罰成本函數進行了智能結合。 2. 實現語言無關緊要

我頗具爭議地使用 JavaScript 開發自動布線器。這是人們最先質疑的點，但實際并非如想象中那般不合理。優化算法時，您本質上需要提升兩個維度：

降低必要迭代次數（提升算法智能度）

提升單次迭代速度

人們往往過度聚焦于第二點。當您采用低效實現方案時（例如將所有元素轉為網格進行重疊檢測），無論使用何種編程語言，執行效率都會令您大失所望！

用最優化的匯編編寫的笨算法，遠不及JavaScript實現的智能算法！

算法 > 語言！

95%的優化精力都應聚焦于減少迭代次數。這才是編程語言無關緊要的根本原因：能讓您最快構建出最智能、最具緩存效率算法的語言，就是最佳實現路徑！

3. 空間哈希索引 > 樹狀數據結構

在多維空間優化領域，四叉樹（QuadTree）可謂無人不知。這種神奇的數據結構能將二維/三維空間中鄰近物體搜索的復雜度從O(N)降為O(log(N))。

但四叉樹及所有通用樹狀數據結構都存在致命缺陷：它們的效率極其低下。樹狀結構本質上無法實現啟發式數據表征。

每當您選擇樹狀結構時，實際上是用復雜度更高的O(log(N))算法替代了復雜度接近O(1)的哈希算法

為何 JavaScript 始終優先采用哈希集合與哈希映射？因為它們擁有絕對性能優勢。空間哈希索引（Spatial Hash Index）的核心理念與哈希映射（HashMap）相同，不同之處在于：我們不再對物體本身進行哈希，而是對其空間坐標進行哈希處理，將其存儲于特定單元（或"空間鄰近物體的集合容器"）

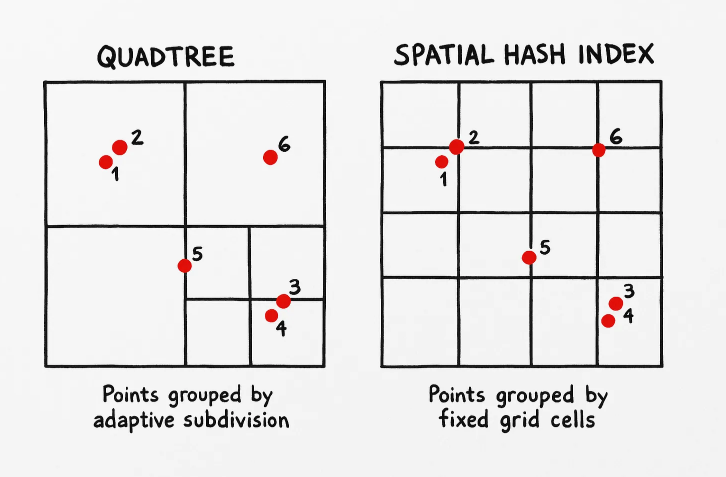
讓我們看看如何用空間哈希索引替換 QuadTree，代碼量只需 20%：

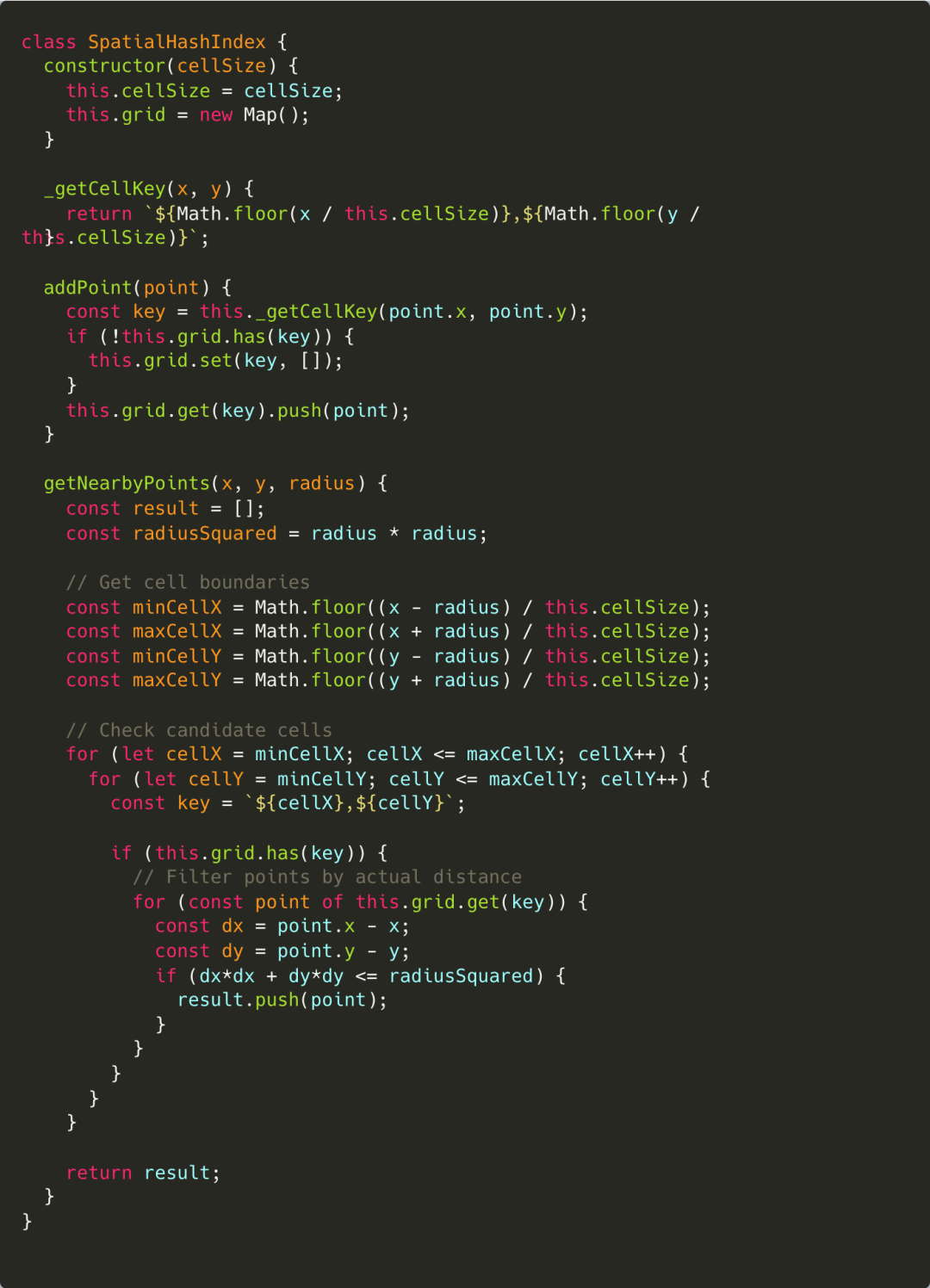
該基礎數據結構存在多種針對不同對象類型的變體，但其核心原理高度相似。我們本質上是通過空間哈希創建"容器"，并將所有位于該哈希對應單元格內的對象填充其中。

空間哈希未能廣受推崇的主因在于：需審慎選擇單元格尺寸：這正是其作為啟發式算法的關鍵所在。若單元格尺寸校準失當，您將承擔高昂的固定檢索成本。但實踐中，選取合理的單元格尺寸并非難事。

4.高效空間分區+緩存機制的重要性是算法性能的1000倍

諸如 iPhone 內部電路板這般精密的設計，通常包含 10,000 至 20,000 條走線，即便使用全球頂尖的 EDA 工具也需要團隊耗費數月完成布線。優化如此復雜的任務看似令人生畏，但事實是整個行業都在忽視一個簡單真理：所有已完成布線的方案都存在歷史復用可能。

游戲開發者會為導航網格"預烘焙"數GB數據。大型語言模型將整個互聯網壓縮為可檢索的權重參數。新一代自動布線器將采用空間分區策略，并調用海量預解決方案的緩存庫。當99%的布線問題已存在預解決方案時，算法本身的執行速度將變得無關緊要。

當前大多數算法并未聚焦于緩存可復用性與空間分區的有效性，但未來自動布線器的核心組件必定是以空間分區方式緩存各階段輸入輸出的解決方案。

更關鍵的是，存儲介質成本下降速度遠超算力提升速度。為自動布線器配置 1GB 緩存實現 50% 提速，在當今技術環境下完全是可行方案。

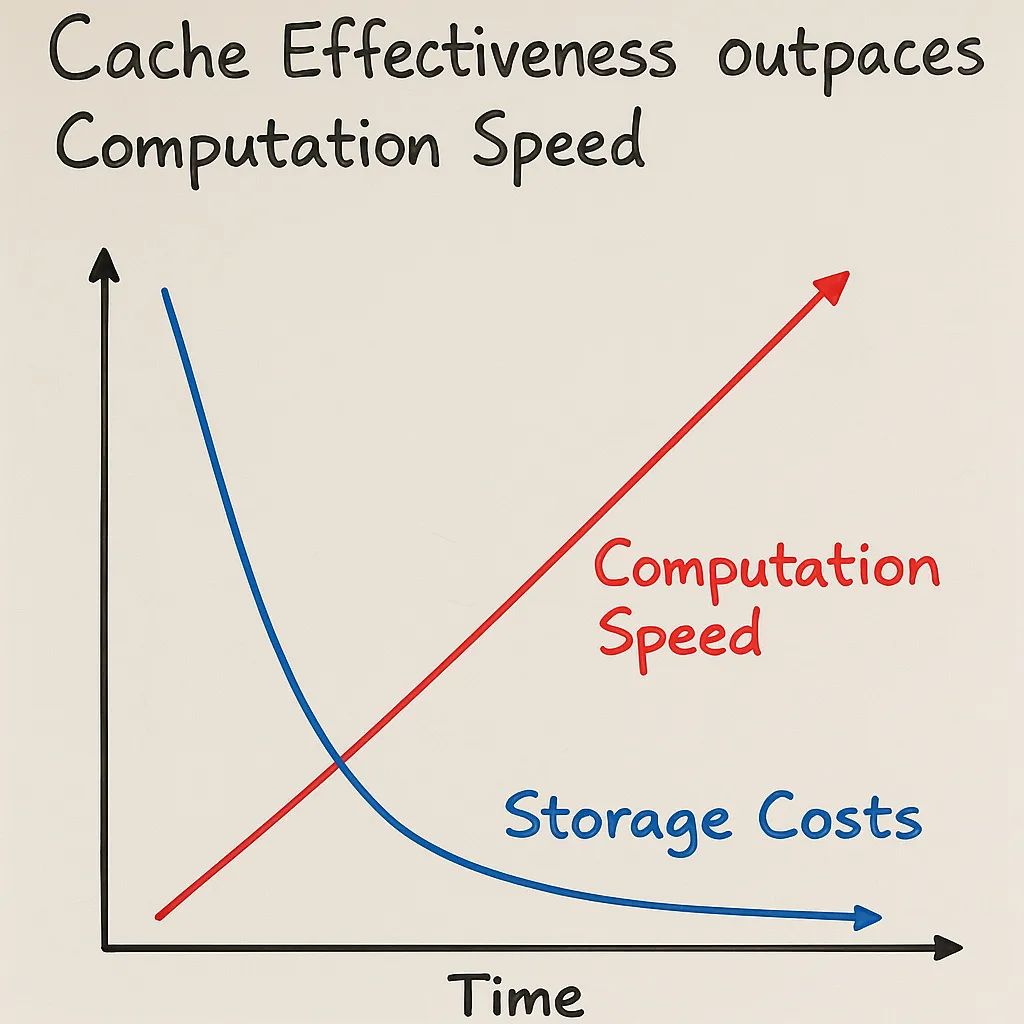
最終，高速緩存將獲勝。可緩存算法比快速算法更重要！

5. 如果問題不能可視化，你可能永遠無法解決

若要將一個技術信條制成海報，我必選擇"問題可視化優先"。僅憑數值分析永遠無法有效調試復雜系統。

我們為每個微小子算法都構建了專屬可視化視圖。開發流程往往始于可視化工具的創建。無數次實踐證明，這種方法能將調試與問題解決效率提升10倍。下圖展示了我們在"路徑簡化階段"（自動布線器近終局階段）中，用于45度路徑探索的子算法可視化方案：

6.JavaScript 性能剖析工具（Profiling）堪稱神器——速速用起來！

JavaScript 性能剖析工具令人驚嘆，您能直觀查看每行代碼消耗的毫秒級執行時長。無需引入任何性能框架，直接在瀏覽器運行代碼后調出性能面板即可。工具還內置火焰圖分析、內存使用分析等強大功能，助您精準定位性能瓶頸。

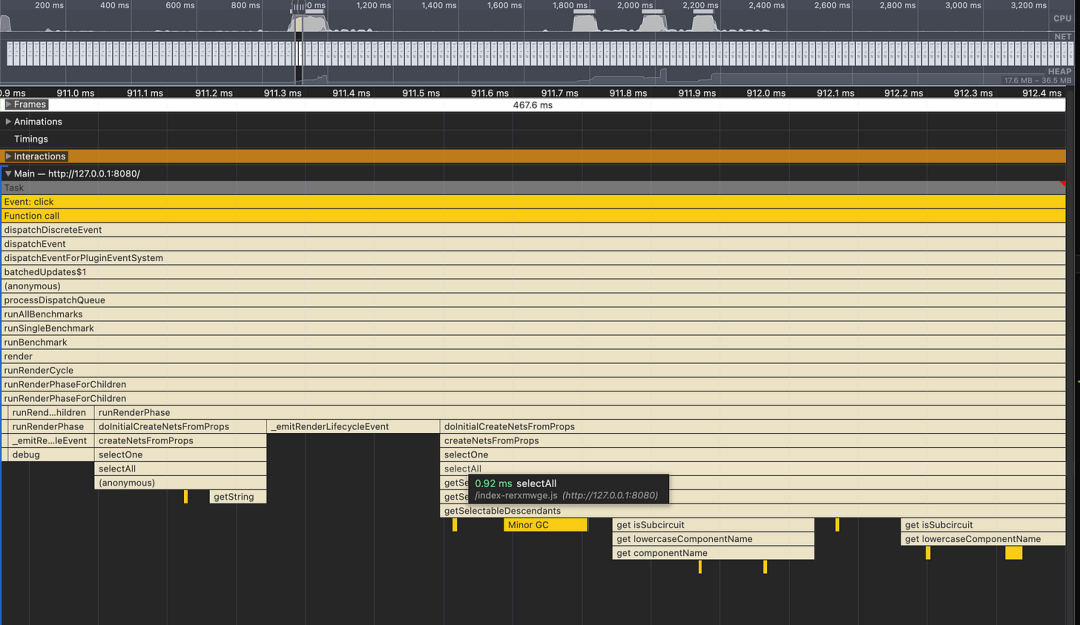
用于調試 @tscircuit/core 中性能的火焰圖分析示例

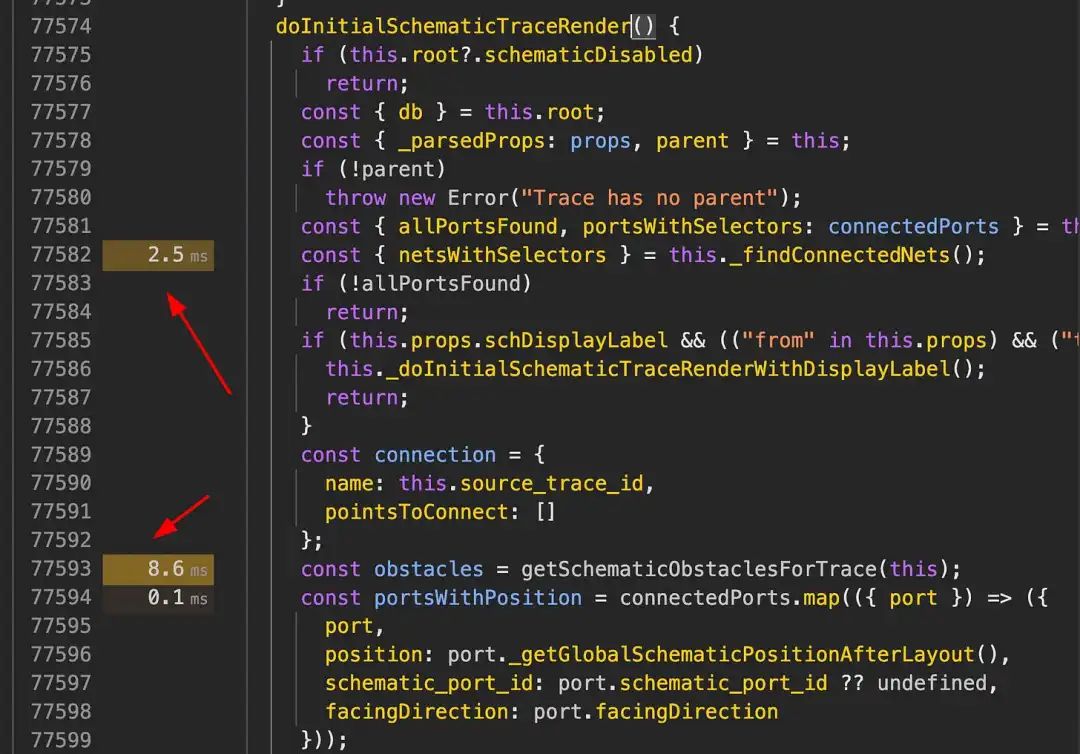
您可以在 Chrome 瀏覽器的性能工具中輕松查看每行代碼所花費的時間！

7. 徹底棄用遞歸函數

遞歸函數存在多重致命缺陷：

? 同步執行特性（無法中斷執行實現動畫效果）

? 本質屬于深度優先搜索（DFS）架構，難以改造為 A* 算法

? 迭代過程難以追蹤與分析

? 可變狀態(Mutability)操作在遞歸中極不自然，卻對性能優化至關重要

以下是將典型遞歸函數重構為非遞歸實現的示例代碼：

基于迭代的實現方案性能顯著提升，關鍵在于其維護了已訪問節點集合(visitedNodes)并在節點探索前執行預檢。雖然遞歸函數理論上也可實現類似機制，但必須通過傳遞可變狀態對象等非自然編碼方式達成。因此在編寫高性能代碼時，強烈建議徹底規避遞歸函數。

8. 像蒙特卡洛算法實屬權宜之計——切勿濫用

蒙特卡洛算法通過隨機采樣逼近解決方案，其本質缺陷在于：

? 催生非確定性算法，大幅增加調試難度

? 相較啟發式策略，永遠無法達成最優解

該算法僅在兩種場景下具有臨時價值：當解決方案路徑未知但評估函數已定義時，可輔助建立基礎認知框架。但一旦構建出近似成本函數，請立即轉向更智能的算法（如模擬退火等隨機優化技術亦需規避）。如果算法容易陷入局部最優陷阱，應通過超參數調優或復合成本函數設計破局：人眼可辨識的局部最優現象，均可轉化為成本函數約束條件。

行業實踐視角佐證：可曾見過PCB工程師在電路板上隨機布線？絕無可能。該領域根本不存在隨機技術的生存空間。啟發式策略的優化空間永無止境。

9. 確保中間算法穩健可靠

當前我們的自動布線器采用13階段處理管線架構，包含約20個可監測迭代次數的子算法模塊。這些模塊分別承擔空間分區判定、邊界路徑簡化等獨立布線區域的專項優化任務。

通過疊加展示各階段算法的輸入輸出可視化視圖，能有效建立問題解決的全局認知框架。實踐中，我們常發現下游階段（特別是"高密度布線階段"）的優化瓶頸，實則可通過提升前置階段的輸出質量實現突破性進展。

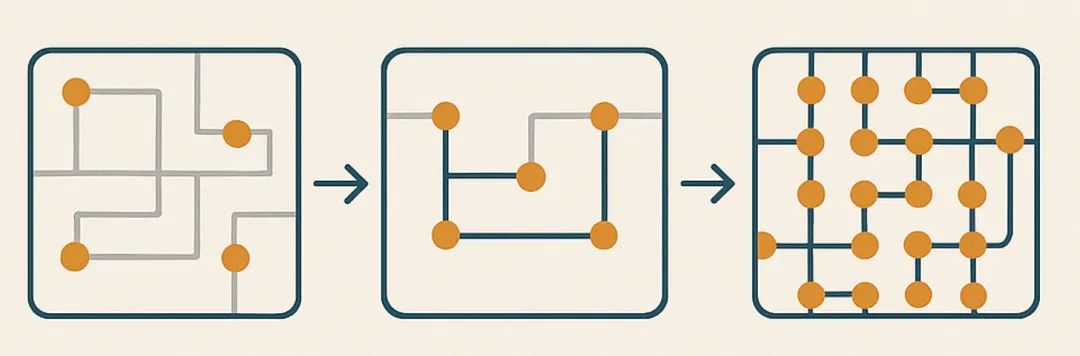
構建子算法時，開發者常傾向于將算法抽象至最簡形態（例如采用以(0,0)為中心的歸一化處理）。但此類坐標變換存在致命風險：可能導致早期算法階段產生的誤差效應難以快速傳導至后續階段進行觀測。解決方案其實很簡單：在整個算法生命周期內保持坐標系絕對一致。 下圖展示了我們各階段算法的串行處理流程：我們常通過深入分析該視圖，精準定位引發設計規則檢查(DRC)失敗的罪魁禍首所在階段。

10.為迭代過程注入動畫洞察，找出愚蠢行為

還記得降低迭代次數至關重要嗎？

通過動畫呈現算法迭代過程，您將直觀感知算法在無關路徑上的無效探索。這種幀級可視化能極大提升對迭代浪費的認知效率。該方法在調節貪心乘數時（詳見第12點）尤其有效。

這段動畫實景演示了一條簡單走線失敗的案例：算法未及時終止，反而持續向外圍無意義擴張。若無動畫輔助，此類異常行為將極難被察覺！

11.交集的數學計算很快，真的需要使用網格嗎？

判斷走線A與走線B是否交疊存在兩種技術路徑：

方案一：逐段解析A/B走線幾何特征，執行向量交集檢測算法

方案二：構建二值化網格標注走線B位置，遍歷走線A覆蓋網格單元進行存在性檢測

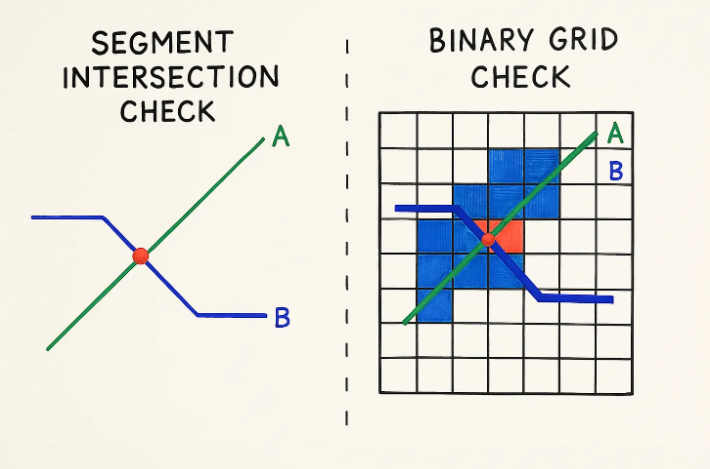
難以置信的是，多數工程師會選擇方案二，即便其性能差距可達千倍！究其根源，竟是數學運算太難了

幸而現代大語言模型使向量交集計算易如反掌。請務必采用高速向量運算方案！須知：檢測單個網格單元（涉及內存訪問！）的實際耗時可能超過執行點積運算完成兩線段交疊判斷的完整計算過程！

12.量化各階段空間失敗概率：可解性優先原則

在解決空間分區問題時，可通過先導指標量化每個處理階段的失敗概率。以 Unravel 自動布線器為例，我們在核心管線階段實時追蹤每個容量節點（Capacity Node）的失敗概率分布。各階段算法通過重構相鄰節點或優化布線路徑，持續降低下游階段的失敗風險。

選擇失敗概率作為核心指標的優勢在于：該指標可量化測量并隨算法改進持續優化。通過逐階段最小化未來失敗概率，形成自適應的優化鏈路。

相較于堆砌過多約束條件，優先保障布線可解性更具戰略價值。當獲得可行解后，基于現有方案迭代優化往往比從零構建最優解更高效。

13.貪婪乘數（Greedy Multiplier）：以最優性換取百倍 A*性能的秘技 嚴格來說這并非機密，或許該稱為"公開的秘密"。但若您尚未掌握此技，則說明尚未發揮 A* 算法的真正威力！ 默認配置下，A*算法保證提供最優解。但若您更追求極速求解而非絕對最優呢？只需對評估函數f(n)做微調，即可獲得加權 A*變體。這種貪婪型優化策略可將求解速度提升數個數量級！

標準A*：f(n) = g(n) + h(n) 加權A*：f(n) = g(n) + w * h(n)

游戲開發者與自動布線工程師面臨諸多共性難題，因此查閱游戲開發領域的技術論文不失為尋找解決方案的捷徑！

原文轉載自https://blog.autorouting.com/p/13-things-i-would-have-told-myself，已經過翻譯及校對

注意：如果想第一時間收到 KiCad 內容推送，請點擊下方的名片，按關注，再設為星標。

常用合集匯總：

和 Dr Peter 一起學 KiCad

KiCad 8 探秘合集

KiCad 使用經驗分享

KiCad 設計項目（Made with KiCad）

常見問題與解決方法

KiCad 開發筆記

插件應用

發布記錄

審核編輯 黃宇