不可能用簡單的RC電路制作逆變器,我們注意到逆變器的重要性,因為這些設備在光伏系統中至關重要。不幸的是,重現一個完美的正弦波形(頻率f0 = 50/60 Hz)非常困難,甚至是不可能的。這意味著必然存在與f0成倍的諧波,如果系統沒有適當屏蔽,這些頻率將產生電磁輻射,從而干擾其他傳輸/接收設備。
積分電路
練習1:考慮施加在具有時間常數τ = RC的積分器電路上的以下輸入:

其中:A = 10 V,τ0 = 1 s是特征時間,T = 8 s是周期。信號行為如圖1所示。該輸入是具有時間常數τ0的阻尼RLC電路的輸出,該電路每8秒回到初始狀態。因此,輸入信號的頻率為f0 = 1/8 Hz。
編寫一個Wolfram機器程序,可以重構輸出信號,區分τ ≠ τ0和τ = τ0的情況。用這樣的設備能否制造逆變器?
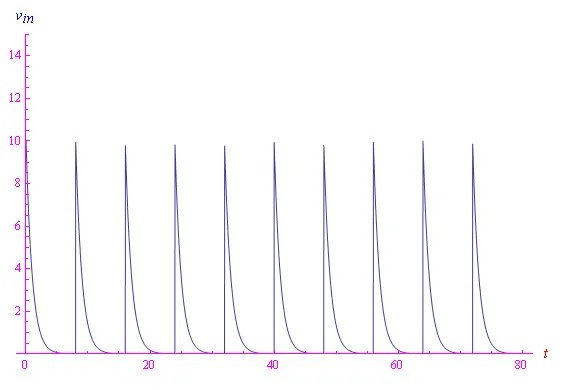 圖1
圖1解析解
這個練習的(表面)困難在于R和C值未知,但它們的乘積RC = τ(自由參數)。在之前的教程中,我們看到由基爾霍夫第二定律導出的微分方程包含時間常數τ和電阻值R,我們還必須添加電荷的初始條件,該條件可能是非零的(在這種情況下,電容器初始是充電的,因為它經歷了先前的瞬態)。
通過解析地解決問題,在最后一步,即計算輸出信號時,變量R消失,因此問題得到解決。然而,直接寫出一個微分方程,其中未知函數不是電容器板上的電荷q(t),而是它們之間的電勢差,即輸出vout,這在計算上更簡單。
這是由于電荷和電容器電容之間的線性關系:q = Cvout。我們邀請讀者執行所有步驟,這些步驟并不復雜,以得出上述必須用顯然的初始條件vout(0) = Cq(0) ≡ v(0)來解決的微分方程。
然而,有趣的情況是電容器初始未充電的情況,此時vout(0) = 0。這樣,僅在初始值下此問題的唯一解在圖2中給出,從中可以看出“積分器電路”這一表達的含義,因為輸入通過一個積分進行處理。
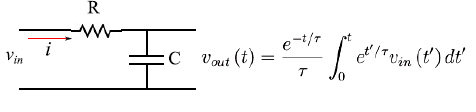 圖2
圖2這里出現一個問題:當積分器電路的時間常數與輸入的時間常數重合時,vout(t)的解析表達式不能使用,因為該表達式返回不確定形式0/0。如所周知,在這種情況下,微分方程在τ = τ0時被重寫,然后進行積分。
在圖3中,我們比較了輸出的趨勢與輸入的趨勢,對于以下τ值,四舍五入到小數點后三位:τ = 0.002,1.002,2.002,3.002 s。注意,第二個值接近τ0。我們因此看到,當τ趨近于零時,輸出趨近于輸入。在相反的極限(τ → +∞)中,輸出趨近于完全為零的信號,正如預期中那樣,因為在這個極限下,電阻或電容趨近于+∞。
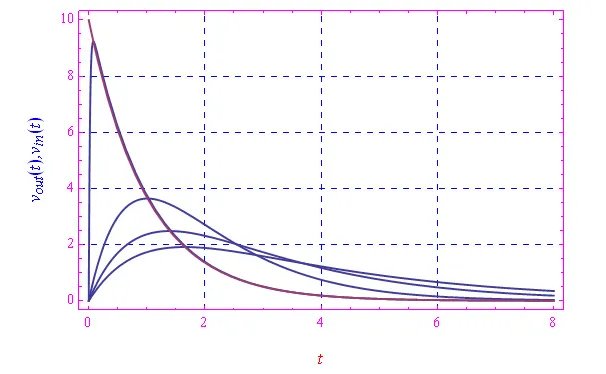 圖3
圖3關于實現逆變器的可能性,答案是否定的,因為這需要一個更復雜的設備。從積分函數的符號(圖2)可以看出這一點,該符號顯然是正的。根據定積分的已知性質,我們得到這樣的符號在[0, t]內定義了積分。
重置微分方程為τ = τ0并求解,我們得到圖4和圖5,其中我們首先在周期性區間比較vout(t)與vin(t),然后在[0, 80 s]內進行比較。
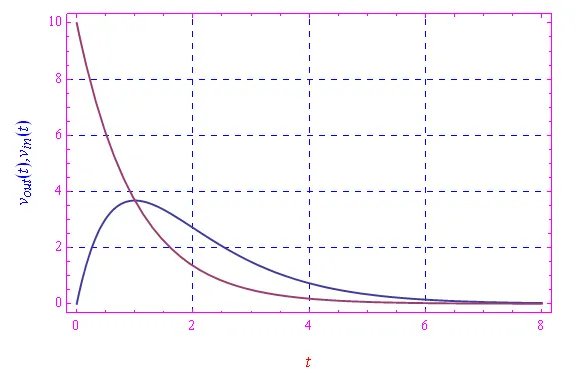 圖4
圖4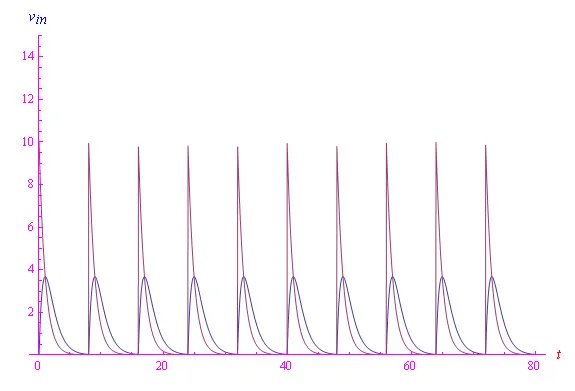 圖5
圖5使用Mathematica的解法
一旦設置了適當的Wolfram機器微分方程,將τ作為自由參數,如果我們嘗試繪制τ = τ0的解,內核將嘗試通過執行除以0的操作來消除不確定形式0/0,隨之而來的是錯誤消息。我們可以將WM分成兩個不同的WM,一個用于τ ≠ τ0,另一個用于τ = τ0,但更優雅的做法是設置一個IF循環,如圖6的屏幕截圖所示,我們突出了相應Mathematica代碼的一些重要方面。
 圖6
圖6關于整個代碼的PDF格式,我們參考文獻1。首先,不能使用延遲賦值“:=”,這告訴內核僅在新輸入調用時確定相應的表達式(函數、指令、其他)。這種類型的賦值用于遞歸程序和緩存技術,但在處理導數等時會產生問題。
例如,如果我們使用延遲賦值來確定某個函數f(x)的導數,然后詢問在某個特定點x0的導數值,內核首先在f(x)的解析表達式中替換x0的值,然后再計算導數,隨之而來的是明顯的錯誤消息(實際上應該為零,因為常數的導數為零)。可以使用強大的Evaluate指令,或者更簡單地使用直接賦值“=”。
對于微分方程而言,情況更復雜,僅使用直接賦值是不夠的,而需要插入Evaluate,我們在后綴表示法中使用它以避免括號的過度使用。代碼被正確解釋,我們通過與解析結果進行比較進行了若干檢查。
關于IF循環,眾所周知,它是傳統編程語言的典型特征,在Mathematica中,其語法如下(*之間的字符串是被內核忽略的注釋條目):
If[ (*condition*) expr, (*then*),
t (*else*) p
]
也就是說,如果expr為真,內核執行t,否則執行p。例如:
復制In[1]=test[x_] := If[ x^3 > 14,
Print[“正確答案。結果為:” , x^3], Print[“錯誤答案”]
]
In[2]=test[2]
錯誤答案
In[3]=test[3]
錯誤答案
正確答案。結果為:216
結論
盡管“封裝”軟件如Mathematica/Maple、Maxima等表現得像一個黑箱,因為它們不允許直接訪問代碼,但在許多應用中,它們極其靈活,允許用幾行代碼解決復雜問題(這種情況是傳統編程語言如Fortran或C無法實現的)。
-
逆變器
+關注
關注
293文章
4860瀏覽量
210122 -
RC電路
+關注
關注
2文章
165瀏覽量
30787
發布評論請先 登錄





 探討RC電路在逆變器設計中的應用與限制
探討RC電路在逆變器設計中的應用與限制










評論