連續(xù)時間系統(tǒng)的復(fù)頻域分析

音頻提綱：（文字簡略而枯燥，語音才更加詳細生動哦）

連續(xù)時間系統(tǒng)的復(fù)頻域分析可以總結(jié)為如下三個方面的內(nèi)容：

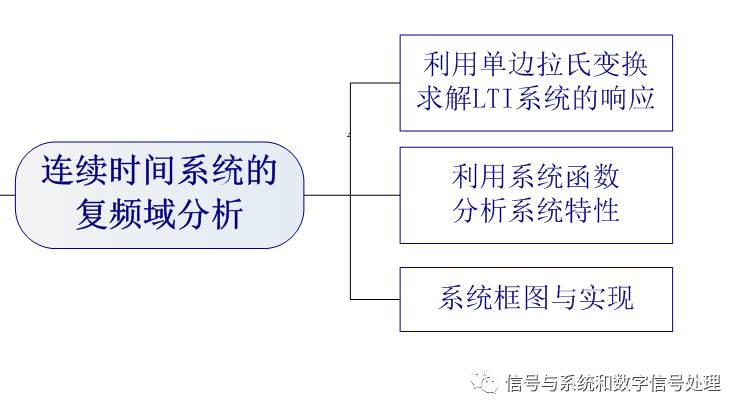
圖1

一、利用單邊拉氏變換求解LTI系統(tǒng)的響應(yīng)

1、微分方程的求解

描述連續(xù)時間LTI的是常系數(shù)的線性微分方程，也就是，由y(t)以及y(t)的各階導(dǎo)數(shù)和x(t)以及x(t)的各階導(dǎo)數(shù)，乘上相應(yīng)的系數(shù)（常數(shù)），加加減減組合成的等式。這個時候，拉氏變換的時域微分特性就大有用武之地了。

方程兩邊取單邊LT，利用LT微分性質(zhì)，就將時域的微分方程，轉(zhuǎn)變成了s域的代數(shù)方程（由X(s)、Y(s)以及系統(tǒng)的初始狀態(tài)y(0-)、y’(0-)......組成），這樣，做一個簡單的代數(shù)運算，就可以求出Y(s)，再求反變換就得到y(t)，這個y(t)是全響應(yīng)。

圖2

如果要分別求解零輸入響應(yīng)和零狀態(tài)響應(yīng)，也很容易。要在求解過程中就分開，看下題，把X(s)放在一堆，初始狀態(tài)y(0-)、y’(0-)......等等放在一堆，那前者就是零狀態(tài)響應(yīng)的拉氏變換，后者就是零輸入響應(yīng)的拉氏變換。

圖3

2、電路系統(tǒng)的求解

當(dāng)然可以先列出電路系統(tǒng)的微分方程，然后利用s域求解方法求解之。但更簡便的方法是，利用電阻、電容、電感的復(fù)頻域等效模型替換，將電路轉(zhuǎn)換為復(fù)頻域的等效電路，直接列出代數(shù)方程。

下圖4是電阻、電容和電感的時域及復(fù)頻域的等效模型。

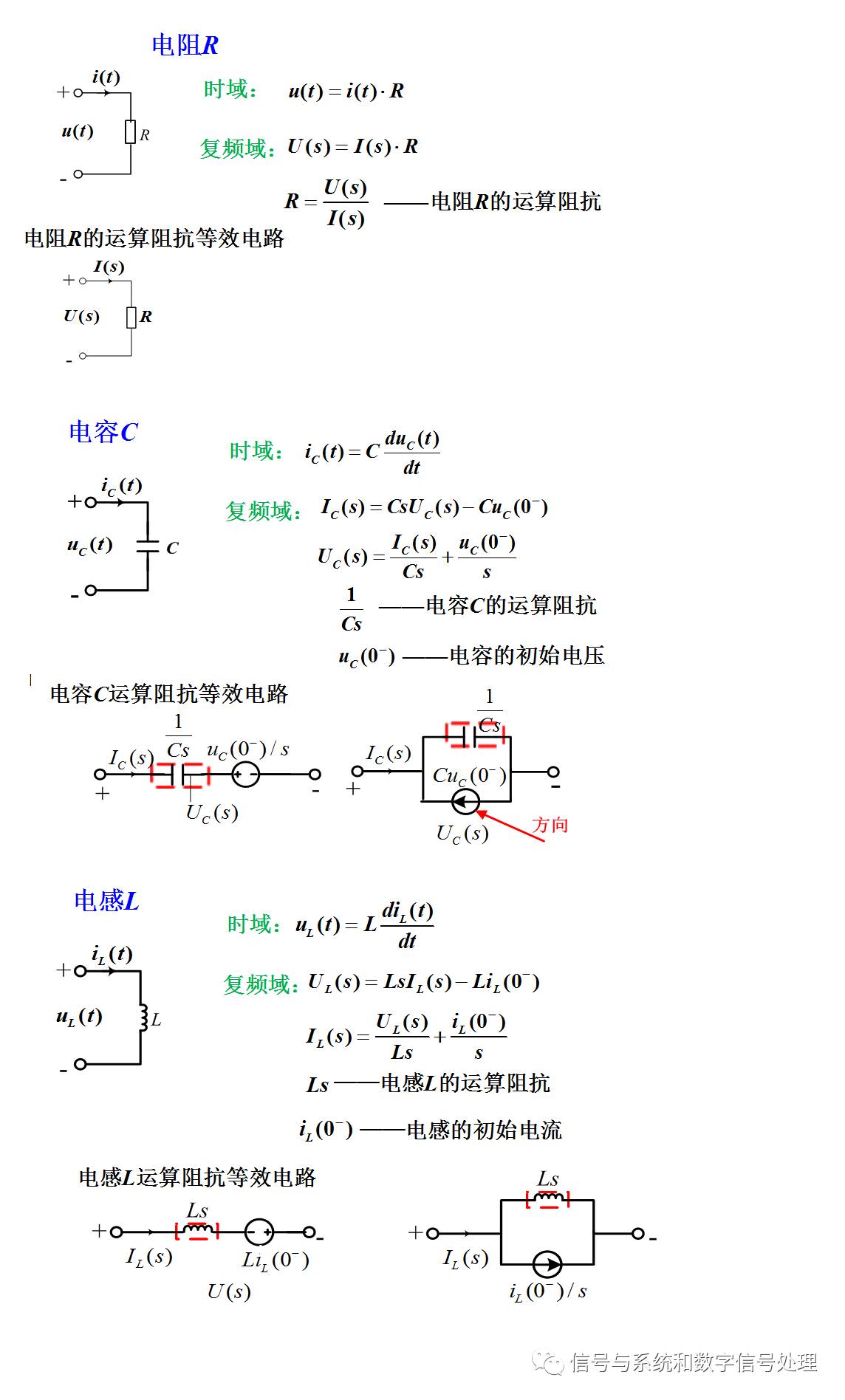
圖4

這樣，將電路系統(tǒng)轉(zhuǎn)換成s域的等效模型之后，利用KVL或KCL列出方程（這個就是代數(shù)方程了），求出Y(s)，再求拉氏反變換即可得出y(t)。

二、利用系統(tǒng)函數(shù)分析系統(tǒng)特性

1、系統(tǒng)函數(shù)

系統(tǒng)函數(shù)H(s)是誰？

H(s)與h(t)的關(guān)系：是單位沖激響應(yīng)h(t)的拉氏變換；

H(s)與輸入/輸出的關(guān)系：是Y(s)/X(s)；

H(s)與H(jw)的關(guān)系：H(jw)=H(s)|s=jw

H(s)與微分方程的關(guān)系：

H(s)與極零點圖的關(guān)系：

H(s)與系統(tǒng)框圖、流圖的關(guān)系：

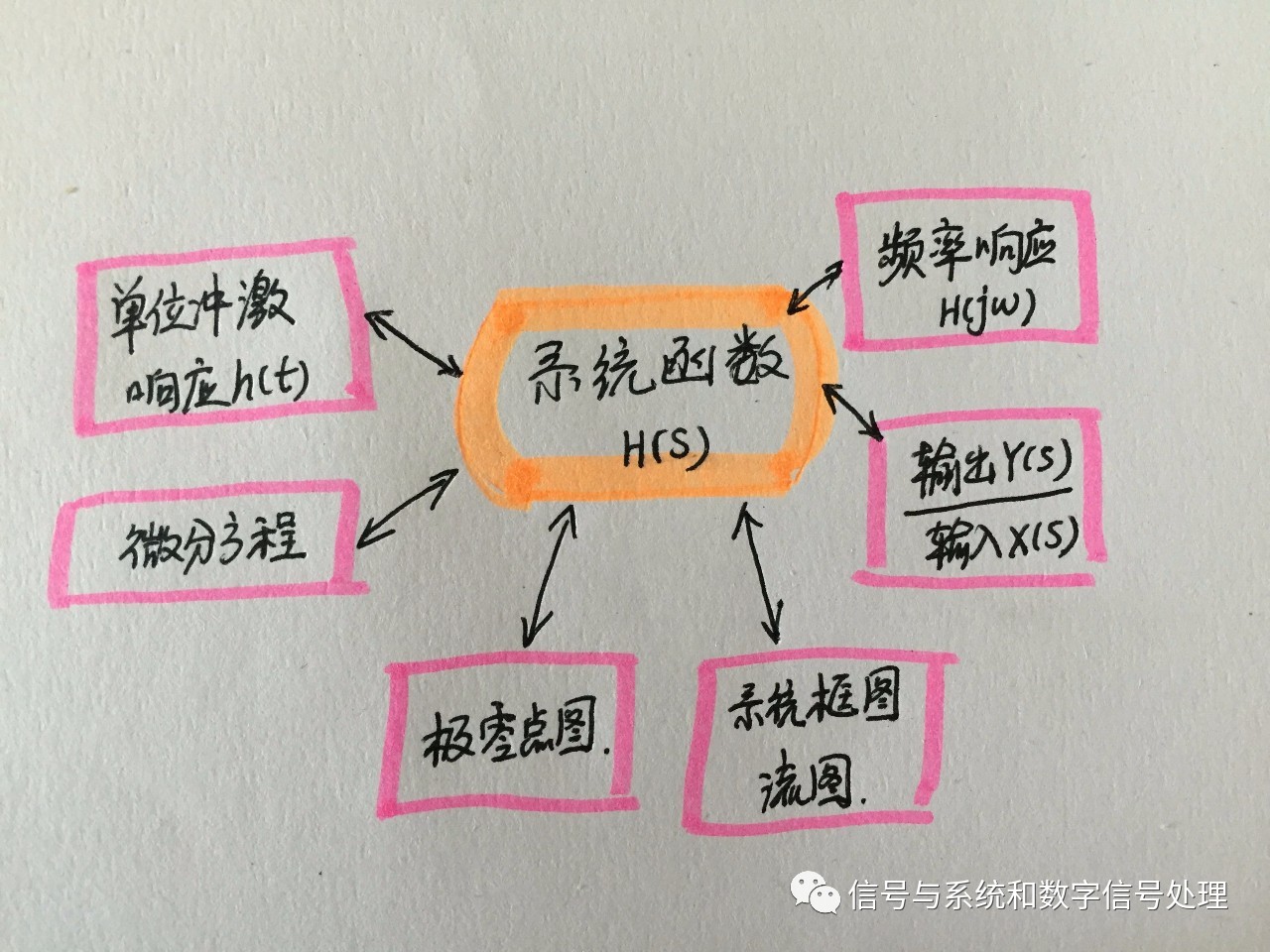
圖5

2、穩(wěn)定性分析

定義：輸入有限，則輸出一定有限（BIBO）

從時域上看：h(t)滿足絕對可積

從復(fù)頻域上看：

收斂域：包含虛軸

極點位置：對于因果系統(tǒng)，所有極點均位于左半平面

勞斯——霍爾維茨準(zhǔn)則（但是需要注意，只適用于判斷連續(xù)時間因果系統(tǒng)的穩(wěn)定性，而且必須計算到n+2行才有意義）

3、系統(tǒng)函數(shù)極零點對濾波器特性的影響

系統(tǒng)的幅頻特性=各零點矢量長度之積/各極點矢量長度之積

系統(tǒng)的相頻特性=各零點矢量相角之和 - 各極點矢量相角之和

極點對幅頻特性的影響——極點增強增益。

極點對頻率選擇性的影響是：使得w0處的增益增強。

隨著極點愈靠近虛軸（a減小），增強效果愈明顯。如果是高階極點，增強效果也愈明顯。

共軛極點的存在并不會顯著改變w0附近的頻率選擇特性。

零點對幅頻特性的影響——零點抵消增益。

零點對頻率選擇性的影響是：使得w0處的增益減小。

隨著零點愈靠近虛軸（a減小），減弱的效果愈明顯。當(dāng)零點在虛軸上時，使w0處增益為零。

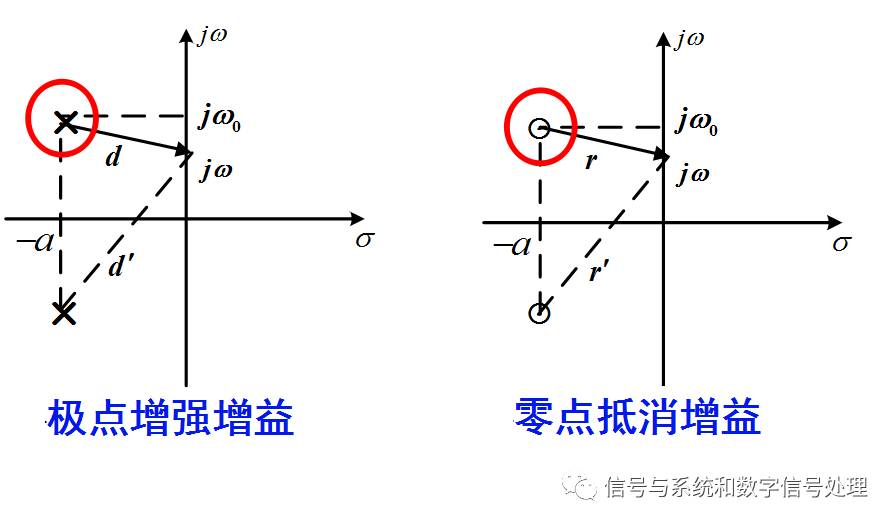
圖6

下面給一個典型了例題，根據(jù)極零點圖判斷系統(tǒng)的濾波特性。

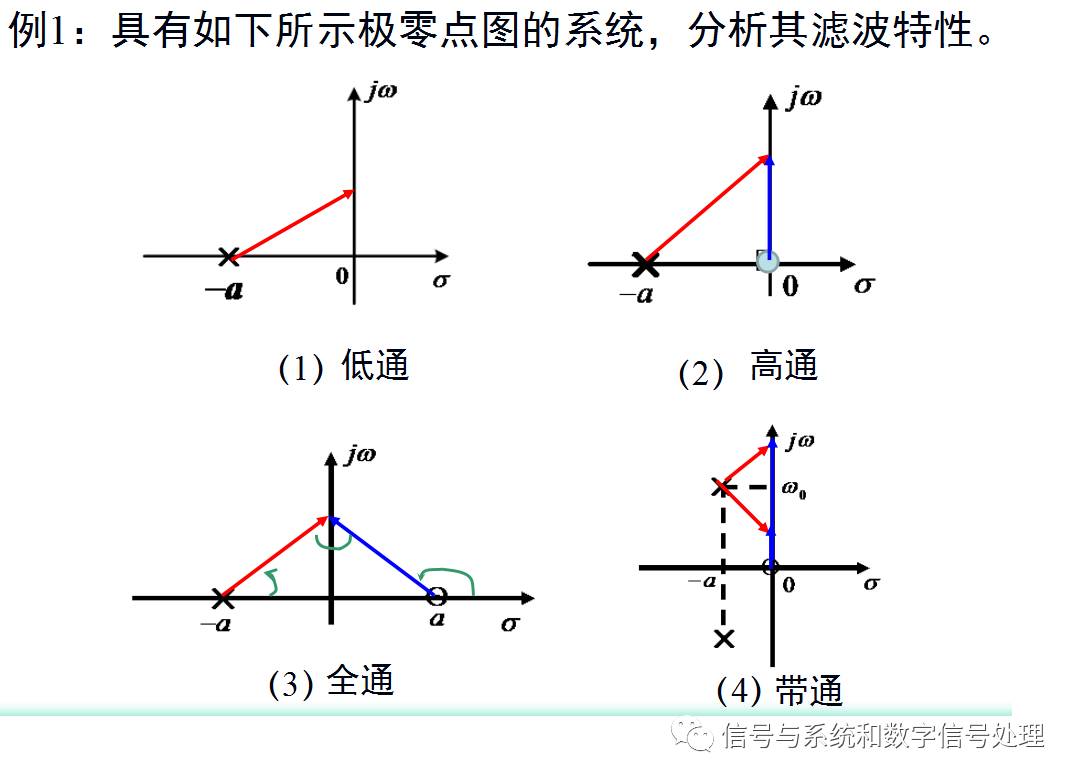
圖7

三、系統(tǒng)框圖與實現(xiàn)

梅森公式是橋梁，可以很方便地在系統(tǒng)函數(shù)和流圖或框圖之間轉(zhuǎn)換。在自動控制、數(shù)字信號處理等課程中也有應(yīng)用。因為內(nèi)容比較簡單，這里不再贅述。