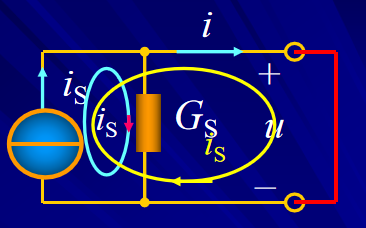
電流源串聯一個電阻的等效電路分析，主要基于電路理論中的“去耦”或“等效變換”原則。在理想情況下（即電流源為無窮大內阻的理想源），串聯的電阻實際上對外部電路沒有影響，因為理想電流源會保持其輸出電流恒定，不受外部電阻變化的影響。但在實際應用中，電流源通常具有一定的內阻，不過為了簡化分析，我們仍可以從理想情況出發進行說明。

理想情況

在理想情況下，電流源的內阻為無窮大，因此串聯的電阻R對外部電路來說可以忽略不計。此時，整個電路（電流源與串聯電阻）可以等效為一個單獨的、具有相同輸出電流的電流源。即，無論串聯電阻的阻值如何，外部看到的都是一個恒定的電流輸出。

實際情況

在實際情況中，電流源具有一定的內阻Ris?。此時，如果電流源串聯一個電阻 R ，那么整個電路的輸出特性將受到這兩個電阻共同影響。然而，從外部電路的角度來看，這個組合仍然可以等效為一個新的電流源，但這個新的電流源將具有一個等效的內阻，該內阻是原電流源內阻Ris?與串聯電阻R的串聯組合。

但需要注意的是，這種等效變換通常用于簡化分析或計算，特別是在進行電路設計時。在實際應用中，如果我們需要精確控制電流或電壓，那么就需要考慮電流源的內阻以及串聯電阻的具體影響。

當電流源串聯一個電阻時，從電路分析的角度來看，這個組合并不能直接等效為一個簡單的電壓源或電流源，因為它們的輸出特性是不同的。然而，在特定的電路變換或等效電路中，我們可以采用一些方法來近似或模擬這種組合的效果。

1. 理想情況與實際情況的對比

• 理想情況 ：在理想情況下，電流源的內阻為無窮大，因此串聯的電阻對外部電路沒有影響。但這種情況在現實中是不存在的，因為所有的電流源都有一定的內阻。
• 實際情況 ：在實際情況中，電流源的內阻和串聯的電阻共同決定了外部電路看到的等效內阻。此時，電流源和串聯電阻的組合可以看作是一個具有特定輸出電流和等效內阻的復合源。

2. 等效變換的考慮

雖然電流源串聯電阻不能直接等效為一個簡單的電壓源或電流源，但在某些情況下，我們可以通過等效變換來近似地表示這種組合的效果。例如：

• 戴維南定理 ：在只關注外部電路（即電流源和串聯電阻組合的輸出端）的情況下，我們可以使用戴維南定理將該組合等效為一個電壓源和一個串聯電阻的組合。這里的等效電壓源電壓等于電流源電流乘以串聯電阻與電流源內阻之和（在理想情況下為串聯電阻），而等效串聯電阻則為電流源的內阻與串聯電阻的串聯組合。但需要注意的是，這種等效只在外部電路與內部電路（即電流源和串聯電阻）沒有直接電氣聯系時成立。
• 諾頓定理 ：在某些情況下，我們可能更希望將電路等效為一個電流源和一個并聯電阻的組合。然而，對于電流源串聯電阻的組合來說，直接應用諾頓定理進行等效變換并不直觀。但我們可以先通過戴維南定理將其等效為一個電壓源和串聯電阻的組合，然后再利用電壓源與電流源之間的等效變換關系（即電壓源可以看作是一個電流源與一個無窮大內阻的并聯組合）來進一步變換。但這種方法在實際應用中并不常見，因為它增加了變換的復雜性和不必要的步驟。

3. 實際應用中的考慮

在實際應用中，我們更關心的是如何根據給定的電流源和串聯電阻來設計或分析外部電路。此時，我們不需要將電流源串聯電阻組合等效為一個簡單的電壓源或電流源，而是可以直接利用它們的實際參數（如電流源的電流、內阻以及串聯電阻的阻值）來進行計算和分析。

結論

綜上所述，電流源串聯一個電阻并不能直接等效為一個簡單的電壓源或電流源。但在特定的電路變換或等效電路中，我們可以采用一些方法來近似或模擬這種組合的效果。在實際應用中，我們更關心的是如何根據給定的參數來設計或分析外部電路。