1. 引言

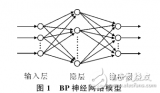
BP神經(jīng)網(wǎng)絡(luò)（Backpropagation Neural Network）是一種前饋神經(jīng)網(wǎng)絡(luò)，通過反向傳播算法進(jìn)行訓(xùn)練。三層BP神經(jīng)網(wǎng)絡(luò)由輸入層、隱藏層和輸出層組成，具有較好的泛化能力和學(xué)習(xí)能力。本文將介紹如何構(gòu)建三層BP神經(jīng)網(wǎng)絡(luò)模型。

2. 神經(jīng)網(wǎng)絡(luò)基礎(chǔ)知識(shí)

2.1 神經(jīng)元模型

神經(jīng)元是神經(jīng)網(wǎng)絡(luò)的基本單元，每個(gè)神經(jīng)元接收輸入信號(hào)，通過激活函數(shù)處理后輸出信號(hào)。一個(gè)神經(jīng)元的數(shù)學(xué)模型可以表示為：

y = f(∑(w_i * x_i + b))

其中，x_i是輸入信號(hào)，w_i是權(quán)重，b是偏置，f是激活函數(shù)。

2.2 激活函數(shù)

激活函數(shù)用于將神經(jīng)元的輸入信號(hào)轉(zhuǎn)換為輸出信號(hào)。常見的激活函數(shù)有Sigmoid函數(shù)、Tanh函數(shù)和ReLU函數(shù)等。Sigmoid函數(shù)的數(shù)學(xué)表達(dá)式為：

f(x) = 1 / (1 + e^(-x))

2.3 損失函數(shù)

損失函數(shù)用于衡量神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)值與真實(shí)值之間的差異。常見的損失函數(shù)有均方誤差（MSE）和交叉熵?fù)p失（Cross-Entropy Loss）等。

3. 三層BP神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)

3.1 輸入層

輸入層是神經(jīng)網(wǎng)絡(luò)的第一層，接收外部輸入信號(hào)。輸入層的神經(jīng)元數(shù)量與問題的特征維度相同。

3.2 隱藏層

隱藏層是神經(jīng)網(wǎng)絡(luò)的中間層，用于提取特征并進(jìn)行非線性變換。隱藏層的神經(jīng)元數(shù)量可以根據(jù)問題的復(fù)雜度進(jìn)行調(diào)整。通常，隱藏層的神經(jīng)元數(shù)量大于輸入層和輸出層的神經(jīng)元數(shù)量。

3.3 輸出層

輸出層是神經(jīng)網(wǎng)絡(luò)的最后一層，用于生成預(yù)測(cè)結(jié)果。輸出層的神經(jīng)元數(shù)量取決于問題的輸出維度。

4. 初始化參數(shù)

在構(gòu)建三層BP神經(jīng)網(wǎng)絡(luò)模型之前，需要初始化網(wǎng)絡(luò)的參數(shù)，包括權(quán)重和偏置。權(quán)重和偏置的初始化方法有以下幾種：

4.1 零初始化

將所有權(quán)重和偏置初始化為0。這種方法簡(jiǎn)單，但可能導(dǎo)致神經(jīng)元輸出相同，無法學(xué)習(xí)有效的特征。

4.2 隨機(jī)初始化

將權(quán)重和偏置初始化為小的隨機(jī)值。這種方法可以避免神經(jīng)元輸出相同，但可能導(dǎo)致梯度消失或梯度爆炸。

4.3 He初始化

He初始化是一種針對(duì)ReLU激活函數(shù)的權(quán)重初始化方法。對(duì)于每一層的權(quán)重矩陣W，其元素W_ij的初始化公式為：

W_ij ~ N(0, sqrt(2 / n_j))

其中，n_j是第j個(gè)神經(jīng)元的輸入數(shù)量。

4.4 Xavier初始化

Xavier初始化是一種針對(duì)Sigmoid和Tanh激活函數(shù)的權(quán)重初始化方法。對(duì)于每一層的權(quán)重矩陣W，其元素W_ij的初始化公式為：

W_ij ~ U(-sqrt(6 / (n_i + n_j)), sqrt(6 / (n_i + n_j)))

其中，n_i是第i個(gè)神經(jīng)元的輸入數(shù)量，n_j是第j個(gè)神經(jīng)元的輸入數(shù)量。

5. 前向傳播

前向傳播是神經(jīng)網(wǎng)絡(luò)從輸入層到輸出層的信號(hào)傳遞過程。在三層BP神經(jīng)網(wǎng)絡(luò)中，前向傳播的過程如下：

5.1 輸入層

將輸入信號(hào)x傳遞給輸入層的神經(jīng)元。

5.2 隱藏層

對(duì)于隱藏層的每個(gè)神經(jīng)元，計(jì)算其輸入加權(quán)和：

z_j = ∑(w_ij * x_i + b_j)

然后，將輸入加權(quán)和通過激活函數(shù)f轉(zhuǎn)換為輸出信號(hào)：

a_j = f(z_j)

5.3 輸出層

對(duì)于輸出層的每個(gè)神經(jīng)元，同樣計(jì)算其輸入加權(quán)和：

z_k = ∑(w_ji * a_j + b_k)

將輸入加權(quán)和通過激活函數(shù)f轉(zhuǎn)換為輸出信號(hào)：

y_k = f(z_k)

6. 反向傳播

反向傳播是神經(jīng)網(wǎng)絡(luò)從輸出層到輸入層的誤差傳遞過程。在三層BP神經(jīng)網(wǎng)絡(luò)中，反向傳播的過程如下：

6.1 計(jì)算損失梯度

首先，計(jì)算輸出層的損失梯度。對(duì)于每個(gè)輸出神經(jīng)元k，損失梯度可以表示為：

d_Lk = ?L / ?z_k = f'(z_k) * (y_k - t_k)

其中，L是損失函數(shù)，t_k是目標(biāo)值。