正是包括兩位菲爾茲獎(jiǎng)獲得者在內(nèi)四位數(shù)學(xué)家的堅(jiān)持，才得以證明了一個(gè)堪稱「加性組合學(xué)圣杯」的猜想，其中 AI 輔助證明起到了不可磨滅的作用。

12 月 5 日，著名數(shù)學(xué)家、菲爾茲獎(jiǎng)獲得者陶哲軒在社交網(wǎng)絡(luò)宣布：對多項(xiàng)式 Freiman-Ruzsa 猜想（PFR）的證明進(jìn)行形式化的 Lean4 項(xiàng)目成功完成，并且耗時(shí)僅三周時(shí)間，其依賴圖的全部節(jié)點(diǎn)都帶上了「可愛的綠色陰影」。

Lean 編譯器也報(bào)告該猜想符合標(biāo)準(zhǔn)公理，可以說這是計(jì)算機(jī)和 AI 輔助證明的一項(xiàng)巨大成功。

但多項(xiàng)式 Freiman-Ruzsa 猜想究竟是什么？為什么對該猜想的證明不僅是一個(gè)數(shù)學(xué)問題，而且對計(jì)算機(jī)科學(xué)也很重要？量子雜志近日報(bào)道了這項(xiàng)成就不凡的數(shù)學(xué)證明及其令人驚嘆的形式化工作，并在文中對多項(xiàng)式 Freiman-Ruzsa 猜想的提出和證明歷程進(jìn)行了梳理與科普。

總結(jié)起來：四位著名數(shù)學(xué)家（包括兩位菲爾茲獎(jiǎng)獲得者）證明了一個(gè)堪稱「加性組合學(xué)圣杯」的猜想。在一個(gè)月的時(shí)間內(nèi)，陶哲軒領(lǐng)導(dǎo)的一個(gè)松散的合作團(tuán)隊(duì)通過計(jì)算機(jī)輔助證明進(jìn)行了驗(yàn)證。

下面就進(jìn)入他們的故事吧。

在一個(gè)隨機(jī)選取的數(shù)值集合中，加法可能會(huì)如野火蔓延，勢不可擋。

對于這樣一個(gè)集合，如果將其中每兩個(gè)數(shù)加起來，就會(huì)得到一個(gè)新的列表并且其中所含的數(shù)值將遠(yuǎn)遠(yuǎn)多于一開始的集合。如果一開始的集合有 10 個(gè)隨機(jī)數(shù)，那么新的列表（稱為和集）會(huì)有大約 50 個(gè)元素。如果一開始是 100 個(gè)隨機(jī)數(shù)，那么和集中可能會(huì)有大約 5000 個(gè)元素；而如果初始有 1000 個(gè)數(shù)，那么和集會(huì)有 50 萬個(gè)數(shù)。

但如果初始集合有結(jié)構(gòu)，則和集中的數(shù)會(huì)少得多。假設(shè)有另一個(gè)包含 10 個(gè)數(shù)的集合：這些數(shù)都是 2 到 20 之間的偶數(shù)。由于不同的一對數(shù)可能會(huì)得到相同的求和結(jié)果（比如 10+12=8+14=6+16），因此和集只會(huì)有 19 個(gè)數(shù)，而非 50 個(gè)。當(dāng)初始集合變得越來越大時(shí)，這一差異也會(huì)越來越顯著。一個(gè)由 1000 個(gè)數(shù)構(gòu)成的結(jié)構(gòu)化列表的和集可能僅會(huì)有 2000 個(gè)數(shù)。

1960 年代，數(shù)學(xué)家 Gregory Freiman 開始研究和集較小的集合，以探究加法和集合結(jié)構(gòu)之間的聯(lián)系 —— 這是定義加性組合學(xué)（additive combinatorics）這一數(shù)學(xué)領(lǐng)域的一個(gè)關(guān)鍵聯(lián)系。Freiman 取得了出色的進(jìn)展，他證明：一個(gè)和集較小的集合必然被包含在一個(gè)更大的集合內(nèi)并且這個(gè)更大集合的元素具有高度規(guī)則的模式。但自那以后，這一領(lǐng)域就停滯不前了。「Freiman 最初的證明非常難以理解，以至于沒人能真正確定它到底是不是正確的。因此它沒有產(chǎn)生應(yīng)有的影響。」法蘭西公學(xué)院和劍橋大學(xué)的數(shù)學(xué)家 Timothy Gowers 說，他也是一位菲爾茲獎(jiǎng)獲得者，「但后來 Imre Ruzsa 突然出現(xiàn)了。」

Ruzsa 在 1990 年代通過兩篇論文用一套優(yōu)雅的新論證重新證明了 Freiman 定理。幾年之后，一位頗具影響力的匈牙利數(shù)學(xué)家 Katalin Marton（已于 2019 年去世）探究了一個(gè)問題：小的和集能夠揭示出原始集合的結(jié)構(gòu)的哪些方面？她替換了該集合中出現(xiàn)的元素的類型與數(shù)學(xué)家應(yīng)當(dāng)找尋的結(jié)構(gòu)的類型，并認(rèn)為這能讓數(shù)學(xué)家提取出更多信息。Marton 的猜想與證明系統(tǒng)、編碼理淪和密碼學(xué)存在關(guān)聯(lián)，并且在加性組合學(xué)領(lǐng)域具有崇高的地位。

Katalin Marton

她的猜想「感覺是我們之前無法理解的最基本的東西之一。」牛津大學(xué)數(shù)學(xué)家 Ben Green 說，「它就是我關(guān)心的很多事情的基礎(chǔ)。」

Green 與 Gowers、加利福尼亞大學(xué)圣迭戈分校的 Freddie Manners 以及加利福尼亞大學(xué)洛杉磯分校的一位菲爾茲獎(jiǎng)獲得者陶哲軒（Terence Tao）組成了一個(gè)團(tuán)隊(duì)。以色列數(shù)學(xué)家和博主 Gil Kalai 將其稱為 A-team，也即數(shù)學(xué)家精英團(tuán)隊(duì)。他們在 11 月 9 日發(fā)布的論文《On a conjecture of Marton》中證明了該猜想的一個(gè)版本。

論文地址：https://arxiv.org/pdf/2311.05762.pdf

未參與該研究的萊斯大學(xué)數(shù)學(xué)家 Nets Katz 描述說這份證明「簡單直接得堪稱美麗」，并且「多少算是完全出乎意料」。

然后陶哲軒開始通過 Lean 來形式化該證明。Lean 是一種可幫助數(shù)學(xué)家驗(yàn)證定理的編程語言。不過幾周時(shí)間，他就成功完成了。12 月 5 日星期二一早，陶哲軒宣布 Lean 已經(jīng)完成對該猜想的證明，并且沒有任何 sorry。sorry 是 Lean 中一個(gè)標(biāo)準(zhǔn)陳述，表示計(jì)算機(jī)無法驗(yàn)證某個(gè)特定步驟。這是自 2021 年以來這樣的證明工具最亮眼的成就，并成為了數(shù)學(xué)家編寫證明的方式的轉(zhuǎn)折點(diǎn)，也就是開始以計(jì)算機(jī)能理解的方式編寫證明。Gowers 說：如果這些工具變得很容易，能讓數(shù)學(xué)家輕松使用，那么它們就可能替代往往耗時(shí)漫長且繁重艱巨的同行評審過程。

這一證明的組分已經(jīng)醞釀了數(shù)十年時(shí)間。Gowers 在 2000 年代構(gòu)想了它的前幾步。但還要另外 20 年，Kalai 所稱的領(lǐng)域「圣杯」才得以證明。

群

為了理解 Marton 猜想，熟悉群（group）的概念會(huì)很有幫助。簡單來說，群是由集合和運(yùn)算構(gòu)成的數(shù)學(xué)對象。這里我們假設(shè)有整數(shù)集（一個(gè)包含無限個(gè)數(shù)的集合）和加法運(yùn)算。我們每次將兩個(gè)整數(shù)相加，便會(huì)得到另一個(gè)整數(shù)。加法也服從其它一些群運(yùn)算規(guī)則，比如結(jié)合律，也就是可以交換運(yùn)算的順序：3 + (5 + 2) = (3 + 5) + 2.

在一個(gè)群內(nèi)，你有時(shí)候可以找到滿足該群所有性質(zhì)的較小集合。舉個(gè)例子，任意兩個(gè)偶數(shù)相加會(huì)得到另一個(gè)偶數(shù)。偶數(shù)本身就是一個(gè)群，這讓其成為了整數(shù)的子群（subgroup）。而奇數(shù)卻不一樣，它并非一個(gè)子群。如果你將兩個(gè)奇數(shù)加到一起，則會(huì)得到一個(gè)偶數(shù) —— 這不在原來的集合中。但只需讓每個(gè)偶數(shù)都加 1，便能得到所有奇數(shù)。像這樣的有移位（shift）的子群稱為陪集（coset）。陪集并不具備子群的所有性質(zhì)，但它又能保留子群在許多方面的的結(jié)構(gòu)。舉個(gè)例子，奇數(shù)和偶數(shù)一樣是均勻分布的。

Timothy Gowers

Marton 猜想如果有一個(gè)由群元素組成的集合 A，其和集并不比 A 本身大很多，那么就會(huì)存在某個(gè)具有一個(gè)特殊性質(zhì)的子群 G。對 G 執(zhí)行幾次移位可以得到一些陪集，而這些陪集組合起來就會(huì)包含原始集合 A。此外，她認(rèn)為陪集的數(shù)量并不會(huì)比和集的大小增長更快 —— 她相信這應(yīng)該是一個(gè)多項(xiàng)式關(guān)系，而非遠(yuǎn)遠(yuǎn)更快的指數(shù)級(jí)增長。

這個(gè)研究方向聽起來可能好像就是為了滿足好奇心，似乎沒什么實(shí)際用途。但由于它和一個(gè)了解子群的總體結(jié)構(gòu)的簡單測試（將集合中的兩個(gè)元素加起來會(huì)發(fā)生什么？）有關(guān)，所以對數(shù)學(xué)家和計(jì)算機(jī)科學(xué)家來說就非常重要了。當(dāng)計(jì)算機(jī)科學(xué)家想要使得加密消息一次只能被解碼一部分時(shí)，也會(huì)遇到這個(gè)想法的廣義版本。它也會(huì)出現(xiàn)在概率可檢驗(yàn)證明（probabilistically checkable proof）中 —— 這種證明形式讓計(jì)算機(jī)科學(xué)家可以通過檢驗(yàn)少量孤立的信息來執(zhí)行驗(yàn)證。

對于上述的每種情況，你只需要研究一個(gè)結(jié)構(gòu)中的一些點(diǎn)，就能得出與一個(gè)更大更高層結(jié)構(gòu)有關(guān)的結(jié)論；比如只需解碼一個(gè)長消息中的少量比特或驗(yàn)證一個(gè)復(fù)雜證明的一小部分。

牛津大學(xué)的 Tom Sanders（他以前是 Gowers 的學(xué)生，現(xiàn)在是 Gowers 的同事）說：「你要么可以假設(shè)一切都是一個(gè)群的一個(gè)大子集，要么可以從許多附加巧合的存在中得到你想要的一切。這兩種觀點(diǎn)都很有用。」

Ruzsa 在 1999 年發(fā)表了 Marton 猜想，并充分說明了她的貢獻(xiàn)和成就。「她獨(dú)立于我和 Freiman 得出了這個(gè)猜想，而且可能先于我們。」他說，「也因此，在我和她交談過之后，我決定用她的名字來命名這個(gè)猜想。」盡管如此，數(shù)學(xué)家現(xiàn)在還是將其稱為多項(xiàng)式 Freiman-Ruzsa 猜想，簡稱 PFR。

零和一

和許多數(shù)學(xué)對象一樣，群也有很多不同的形式。Marton 猜測她的猜想對所有群都成立。這一點(diǎn)還有待證明。這篇新論文證明其對某一特定類型的群成立，這類群的元素是 (0, 1, 1, 1, 0) 這樣的二進(jìn)制數(shù)列表。由于計(jì)算機(jī)的工作過程就基于二進(jìn)制，因此這個(gè)群對計(jì)算機(jī)科學(xué)至關(guān)重要。但它也對加性組合學(xué)很有用。「它就像是一個(gè)玩具設(shè)置，你可以在其中玩耍，嘗試各種東西。」Sanders 說，「這里的代數(shù)操作起來比非負(fù)整數(shù)（whole number）容易太多了。」

陶哲軒

這些列表的長度是固定的，而且每一位都要么為 0，要么為 1。這樣的兩個(gè)列表相加就是將一個(gè)列表的每一項(xiàng)與另一列表的對應(yīng)項(xiàng)相加，規(guī)則包括 1 + 1 = 0。那么 (0, 1, 1, 1, 0) + (1, 1, 1, 1, 1) = (1, 0, 0, 0, 1)。PFR 試圖搞清楚：如果一個(gè)集合算不上是子群，但具有某些類似群的特征，那么這個(gè)集合看起來會(huì)是什么樣。

為了更清楚地說明 PFR，請想象一下你有一個(gè)二元列表構(gòu)成的集合 A。現(xiàn)在從 A 中取出每一對元素并相加。所得到的和可構(gòu)成 A 的和集，記為 A+A。如果 A 中的元素是隨機(jī)選取的，那么大部分的和都彼此不同。如果 A 有 k 個(gè)元素，那就意味著和集有 k2/2 個(gè)元素。當(dāng) k 很大時(shí)（比如 1000），k2/2 就會(huì)比 k 大很多。但如果 A 是一個(gè)子群，那么 A+A 的每個(gè)元素都在 A 中，這就意味著 A+A 的大小和 A 本身是一樣的。

PFR 考慮的集合不是隨機(jī)的，但也不是子群。在這些集合中，A+A 的元素?cái)?shù)量會(huì)有些小，比如 1 萬或 10 萬。加利福尼亞大學(xué)圣迭戈分校的計(jì)算機(jī)科學(xué)家 Shachar Lovett 說：「當(dāng)你的結(jié)構(gòu)概念比僅僅作為精確的代數(shù)結(jié)構(gòu)豐富得多時(shí)，這真的會(huì)很有用。」

就數(shù)學(xué)家所知，所有服從這一性質(zhì)的集合「都相當(dāng)接近于真正的子群。」陶哲軒說，「這是一個(gè)直覺認(rèn)識(shí)，也就是沒有其它類型的假群存在。」Freiman 在其原研究成果中證明了這一命題的一個(gè)版本。1999 年時(shí)，Ruzsa 將 Freiman 定理從整數(shù)擴(kuò)展到了二元列表設(shè)置。他證明，當(dāng) A+A 的元素?cái)?shù)量是 A 的大小的常數(shù)倍時(shí)，A 必定被包含在一個(gè)子群內(nèi)。

但 Ruzsa 定理需要子群非常巨大才行。Marton 的見解是假定 A 不是包含在一個(gè)巨大的子群中，而是可以包含在一個(gè)子群的多項(xiàng)式數(shù)量的陪集中并且這個(gè)子集不大于原始集合 A。

好想法看一眼就知道

千年之交那段時(shí)間，Gowers 在研究與包含均勻相間的字符串的集合相關(guān)的另一問題時(shí)看到了 Ruzsa 對 Freiman 定理的證明。「我就需要這樣的東西，差不多就是從有關(guān)一個(gè)特定集合的松散得多的信息中獲取結(jié)構(gòu)化信息。」Gowers 說，「我非常幸運(yùn)，就在那不久前，Ruzsa 剛給出這個(gè)美不勝收的證明。」

Freddie Manners

Gowers 開始著手嘗試證明該猜想的多項(xiàng)式版本。他的想法是先從和集相對較小的集合 A 開始，然后逐漸操作 A，將其變成一個(gè)子群。如果他能證明所得子群與原始集合 A 相似，他就可以輕松斷定這個(gè)猜想是正確的。Gowers 將這個(gè)想法分享給了自己的同事，但沒人能將其轉(zhuǎn)化成完整的證明。盡管 Gowers 的策略能成功處理一些情況，但在其它情況中，這種操作卻會(huì)讓 A 更加遠(yuǎn)離多項(xiàng)式 Freiman-Ruzsa 猜想的預(yù)期結(jié)論。

最終，該領(lǐng)域放棄了這一思路。2012 年，Sanders 幾乎證明了 PFR。但他需要的移位子群的數(shù)量高于多項(xiàng)式水平，盡管只高一點(diǎn)點(diǎn)。Gowers 說，「一旦他做到了，就意味著這事件變得不那么緊迫了，但這仍然是一個(gè)我非常喜歡的好問題。」

但 Gowers 的想法依然留存在他同事的記憶和硬盤中。「那是一個(gè)真正的好想法。」Green 說，他也曾是 Gowers 的學(xué)生，「好想法看一眼就知道。」今年夏季，Green、Manners 和陶哲軒終于將 Gowers 的想法從煉獄中解放了出來。

在決定研究已有 20 年歷史的 Gowers 想法之前，Green、陶哲軒和 Manners 的合作成果已經(jīng)可以羅列 37 頁之長。在 6 月 23 日的論文《Sumsets and entropy revisited》中，他們成功使用了概率論中的「隨機(jī)變量」概念來探測具有小和集的集合的結(jié)構(gòu)。通過這種切換，該團(tuán)隊(duì)可以更巧妙地操作集合。「處理隨機(jī)變量在某種程度上比處理集合要簡單得多。」Manners 說，「對于隨機(jī)變量，我可以稍微調(diào)整其中一個(gè)概率，而這就可能會(huì)給我一個(gè)更好的隨機(jī)變量。」

從這個(gè)概率角度入手，Green、Manners 和陶哲軒可以不用再面對一個(gè)集合的元素?cái)?shù)量，而是可以去衡量一個(gè)隨機(jī)變量中所包含的信息，這個(gè)量被稱為熵（entropy）。對加性組合學(xué)來說，熵并不是新東西。事實(shí)上，陶哲軒在 2000 年代末就嘗試過推廣這一概念。但還沒有人試過將其用于多項(xiàng)式 Freiman-Ruzsa 猜想。Green、Manners 和陶哲軒發(fā)現(xiàn)它很強(qiáng)。但他們?nèi)匀徊荒茏C明該猜想。

Ben Green

當(dāng)這個(gè)研究團(tuán)隊(duì)仔細(xì)研究他們的新成果時(shí)，他們意識(shí)到終于建立了一個(gè)可讓 Gowers 那蟄伏的想法重獲新生的環(huán)境。如果使用集合的熵來衡量集合的大小，而不是元素?cái)?shù)量，則其技術(shù)細(xì)節(jié)可能會(huì)好處理得多。「某一時(shí)刻我們意識(shí)到，比起我們當(dāng)時(shí)正在嘗試的思路，這些來自 Tim 的 20 年前的舊想法實(shí)際上更可能有效。」陶哲軒說，「于是我們把 Tim 帶回了這個(gè)項(xiàng)目。然后所有的碎片都出人意料地很好地拼合在了一起。」

盡管如此，在給出完整的證明前，還有很多細(xì)節(jié)要處理。「我們四個(gè)人都還各自忙著其它事，這是有點(diǎn)愚蠢的。」Manners 說，「你希望發(fā)表這個(gè)偉大的結(jié)果并且告訴全世界，但你實(shí)際上還依然必須要去寫期中報(bào)告。」最終，這個(gè)團(tuán)隊(duì)堅(jiān)持了下來，并于 11 月 9 日發(fā)表了論文。他們證明，如果 A+A 不大于 A 的大小的 k 倍，那么可通過一個(gè)不大于 A 的子群的不超過 k12 移位而將 A 覆蓋其中。這個(gè)移位的數(shù)量很可能非常大。但這是一個(gè)多項(xiàng)式，不會(huì)隨 k 的增大而指數(shù)級(jí)增長；而如果 k 在指數(shù)中就會(huì)這樣。

幾天之后，陶哲軒開始形式化該證明。他以協(xié)作的方式運(yùn)行了這個(gè)形式化項(xiàng)目，使用了版本控制軟件包 GitHub 來協(xié)調(diào)來自全球 25 個(gè)志愿者的貢獻(xiàn)。他們使用了一種名為 Blueprint 的工具。這個(gè)工具是巴黎薩克雷大學(xué)數(shù)學(xué)家 Patrick Massot 開發(fā)的，可用于協(xié)調(diào)組織將陶哲軒所說的「數(shù)學(xué)式英語」翻譯成計(jì)算機(jī)代碼的工作。Blueprint 的功能有很多，其中之一是創(chuàng)建一張圖表來描述證明中涉及的各種邏輯步驟。一旦圖中所有氣泡都變成陶哲軒所說的「可愛的綠色陰影」，這個(gè)團(tuán)隊(duì)就算完工了。

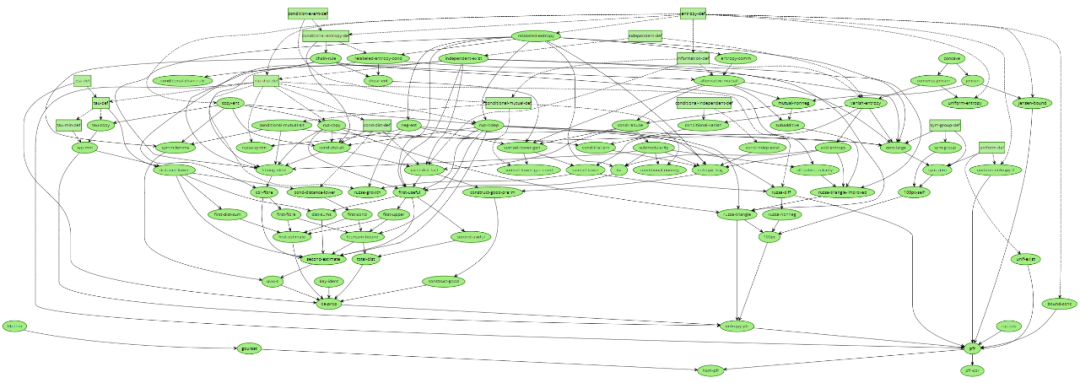
對 PFR 猜想的證明的依賴圖，其中方框是定義，橢圓是定理和引理，全部背景都是綠色說明該證明已經(jīng)完全形式化

他們發(fā)現(xiàn)論文中存在一些非常小的拼寫錯(cuò)誤 —— 在一條網(wǎng)絡(luò)消息中，陶哲軒指出：「這個(gè)項(xiàng)目中與數(shù)學(xué)最相關(guān)的部分的形式化是相對簡單直接的，但技術(shù)上『顯而易見』的步驟反而耗時(shí)最長。」

Marton 在她的著名猜想得到證明的幾年前去世了，但這個(gè)證明幫助彰顯了她在熵和信息論領(lǐng)域的畢生成就。「當(dāng)使用這個(gè)熵框架進(jìn)行研究，而不是我之前嘗試的框架時(shí)，一切都好了很多。」