來源 | 《趣學貝葉斯統計:橡皮鴨、樂高和星球大戰中的統計學》 作者 | [美] 威爾·庫爾特(Will Kurt) 譯者 |王凌云
本章將概述貝葉斯推理。所謂貝葉斯推理,是指我們在觀察到一些數據后,更新自己對這個世界的信念的過程。我們將通過一個場景來探討如何將日常經驗映射到貝葉斯推理中。
好消息是,在拿起本書之前,你就已經是一個貝葉斯主義者了!貝葉斯統計其實與人們如何自然地利用數據創造新的信念、如何進行日常問題的推理密切相關。壞消息是,將這種自然的思維過程分解為嚴謹的數學過程很難。
在統計學中,我們通過使用特定的計算和模型來更準確地量化概率。不過,本章不會使用任何數學計算或模型,我們只需要熟悉基本概念,并利用直覺來確定概率。我們才會精確地計算概率。在本書的剩余部分,你將學習如何使用嚴格的數學方法對本章涉及的概念進行形式化的建模和推理。
1 對奇怪經歷的推理
一天晚上,你突然被窗外的一道亮光驚醒。你從床上跳起來,向外望去,發現天空中有一個碟形的龐然大物。你從來都不相信會遇見外星人,但現在你完全被外面的景象迷惑了。你發現自己在想:這難道是不明飛行物(unidentified flying object,UFO)嗎?!
貝葉斯推理就是這樣一種思維過程:在遇到一種情況時,你會做出概率假設,然后根據這些假設更新你對這個世界的信念。在UFO這個情景中,你已經經歷了一個完整的貝葉斯分析過程,因為你:
(1) 觀察到了數據;
(2) 做出了一個假設;
(3) 根據觀察到的數據更新了自己的信念。
這種推理往往發生得太快,以至于你沒有時間分析自己的思維過程。你在沒有任何質疑的情況下建立了一個新的信念:之前你不相信UFO的存在,在事件發生之后你更新了自己的信念,你認為自己看到了UFO。
本章主要關注信念的產生及其構建過程,這樣你就可以更規范地研究它。此外,后面的章節還將研究如何量化這個過程。
讓我們從觀察數據開始,依次分析這個推理過程的每一個步驟。
(1)觀察數據
將信念建立在數據上,是貝葉斯推理的一個關鍵組成部分。在對場景得出任何結論之前(比如說你聲稱自己看到了UFO),你需要理解所觀察到的數據。在這個例子中,數據是:
窗外的一道亮光;
一個碟形物體在空中盤旋。
根據經驗,你會把窗外的景象描述為“令人驚訝的場景”,用概率的術語表示,可以將它寫為:
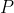 (窗外出現亮光, 天空中有碟形物體)?
(窗外出現亮光, 天空中有碟形物體)? ?很小
?很小
其中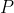 ?表示概率,括號內列出的是兩條數據。你可以將這個等式理解為“窗外出現亮光且天空中有碟形物體的概率很小”。在概率論中,當要表示多個事件的聯合概率(combined probability)時,用逗號分隔事件。請注意,這兩條數據并不包含任何關于UFO的具體內容,它只由你的觀察結果組成——這一點在后面會很重要。
?表示概率,括號內列出的是兩條數據。你可以將這個等式理解為“窗外出現亮光且天空中有碟形物體的概率很小”。在概率論中,當要表示多個事件的聯合概率(combined probability)時,用逗號分隔事件。請注意,這兩條數據并不包含任何關于UFO的具體內容,它只由你的觀察結果組成——這一點在后面會很重要。
也可以考查單個事件的概率,并將其寫為:
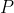 (下雨)?
(下雨)? ?很可能
?很可能
這個等式的意思是,“下雨的概率比較大”。
對剛才提到的UFO場景,我們要確定的是兩個事件一起發生的概率。這與兩個事件單獨發生的概率完全不同。例如,單獨出現亮光很容易,一輛路過的汽車就會發出亮光,所以就出現亮光這個事件而言,它發生的概率要遠遠大于它和碟形物體同時出現的概率(不過碟形物體單獨出現也同樣讓人驚訝)。
如何確定這個概率呢?現在,我們使用的是直覺,也就是自我感覺到的這件事發生的可能性。第2章將介紹如何得出概率的精確數值。
(2)先驗信念和條件概率
早晨醒來,煮杯咖啡喝,然后開車去上班。在這個過程中,你不需要做很多分析,這是因為你對這個世界如何運轉有著先驗信念(prior belief)。先驗信念是我們根據一生的經驗(也就是觀察到的數據)建立起來的信念集合。你相信太陽會升起,因為自你出生以來太陽每天都會升起(當然,在陰雨天,你看不見太陽升起)。如果沒有先驗信念,我們每天晚上睡覺時都會害怕明天的太陽可能不會升起。
先驗信念表示,在看到窗外有明亮燈光的同時看到一個碟形物體,這在地球上很少見。但如果你生活在一個遙遠的星球上,那里有大量的飛碟且經常有星際訪客,那么在天空中同時看到亮光和碟形物體的概率就會大很多。
在公式中,先驗信念寫在數據后面并用“|”與數據隔開,就像下面這樣:
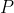 (窗外出現亮光,天空中有碟形物體 | 地球上的經驗)?
(窗外出現亮光,天空中有碟形物體 | 地球上的經驗)? ?很小
?很小
這個等式可以理解為:“根據我們在地球上的經驗,在天空中同時看到亮光和碟形物體的概率很小。”
這個概率結果被稱為條件概率(conditional probability),因為計算某一個事件發生的概率時,以另一個事件的存在為條件。在這種情況下,我們會根據經驗來調整觀察到的事件的概率。
正如用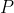 ?表示概率一樣,我們通常用另外的變量來表示事件和條件,這樣更簡潔。如果你不太熟悉等式,一開始可能覺得它們顯得過于簡潔。但過一段時間你就會發現,簡潔的變量名既有助于提高可讀性,也有助于你了解等式如何推廣到更大的問題類別上。我們將把所有的數據賦給一個變量?
?表示概率一樣,我們通常用另外的變量來表示事件和條件,這樣更簡潔。如果你不太熟悉等式,一開始可能覺得它們顯得過于簡潔。但過一段時間你就會發現,簡潔的變量名既有助于提高可讀性,也有助于你了解等式如何推廣到更大的問題類別上。我們將把所有的數據賦給一個變量?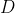 :
:
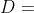 ?窗外出現亮光,天空中有碟形物體
?窗外出現亮光,天空中有碟形物體
所以從現在開始,當提到這組數據集的概率時,我們會直接用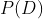 ?來表示。
?來表示。
同樣,我們會用變量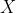 ?來表示先驗信念,像下面這樣:
?來表示先驗信念,像下面這樣:
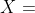 ?地球上的經驗
?地球上的經驗
現在可以將上文中等式的左邊寫為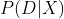 。這樣寫更為簡單且意思保持不變。
。這樣寫更為簡單且意思保持不變。
以多重信念為條件
如果有一個以上的變量會顯著影響概率,那么我們可以添加一個以上的先驗信念。假設今天是特定節日,根據經驗,你知道在這天放煙花很常見。根據你在地球上的經驗和今天是特殊的日子,在天空中看到亮光的概率不是完全沒有,甚至那個碟形物體也可能與某個煙花表演有關。因此,你可以將這個等式改寫為:
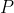 (窗外出現亮光, 天空中有碟形物體 | 特定節日, 地球上的經驗)?
(窗外出現亮光, 天空中有碟形物體 | 特定節日, 地球上的經驗)? ?小
?小
對比這兩種情況可以發現,條件概率從“很小”變成了“小”。
在實踐中假設存在先驗信念
在統計學中,通常不會明確地為所有的現有經驗附加條件,因為它是可以假設的。出于這個原因,在本書中,我們不會在這種情況下單獨增加變量。然而在貝葉斯分析中,我們必須記住,我們對這個世界的理解總是以自己在這個世界上的經驗為條件的。本章的其余部分會保留“地球上的經驗”這個變量以提醒這一點。
(3)形成假設
到目前為止,我們已經有了數據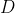 (看到了一道亮光和一個碟形物體)和先驗信念?
(看到了一道亮光和一個碟形物體)和先驗信念?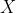 。為了解釋所看到的情況,我們需要形成某種假設(hypothesis),即形成一個關于世界如何運作的模型,從而做出預測。假設可以有多種形式,我們對這個世界的所有基本信念都可以是假設。
。為了解釋所看到的情況,我們需要形成某種假設(hypothesis),即形成一個關于世界如何運作的模型,從而做出預測。假設可以有多種形式,我們對這個世界的所有基本信念都可以是假設。
如果相信地球自轉,那么你就可以預測太陽會在某個時間升起和落下。
如果認為你最喜歡的棒球隊是最好的,那么你就可以預測他們會比其他球隊贏得更多。
假設也可以更正式、更復雜。
科學家可能會假設某種治療方法能減緩癌癥惡化。
金融領域的定量分析師會構建市場行為模型。
深度神經網絡可以預測哪些圖像展示的是動物,哪些圖像展示的是植物。
所有這些例子都是假設,因為它們都包含對這個世界的某種理解,并利用這種理解來預測世界將如何運作。當提到貝葉斯統計中的假設時,通常關注的是它對我們觀察到的數據的預測能力。
當看到數據并認為自己看到了UFO時,你就在形成一個假設。UFO的假設很可能是基于你以前看過的電影和電視節目。將第一個假設定義為:
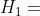 ?在我家的后院里有一個UFO!
?在我家的后院里有一個UFO!
但這個假設預測的又是什么呢?如果將問題倒過來想,我們可能會問:“如果在你家的后院里有一個UFO,那么你預期會看到什么呢?”你可能會回答:“亮光和碟形物體。”因為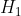 ?預測了數據?
?預測了數據?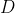 ,所以當我們在給定的假設下觀察到數據時,數據的概率就會增加。這樣的結果可以規范地表示為:
,所以當我們在給定的假設下觀察到數據時,數據的概率就會增加。這樣的結果可以規范地表示為:
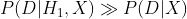
這個式子的意思是:“如果相信這是UFO并根據經驗,在天空中看到亮光和碟形物體的概率要遠遠大于只看到亮光和碟形物體而無法解釋的概率(這里用兩個大于號 ?表示遠遠大于)。”這里用概率的語言證明了我們的假設可以解釋數據。
?表示遠遠大于)。”這里用概率的語言證明了我們的假設可以解釋數據。
(4)在日常語言中發現假設
很容易看出,日常語言和概率之間有著某種關系。例如,說某事“令人驚訝”,其實就等于說,根據我們的經驗,它發生的概率比較小;而說某件事“很合理”,其實是說,基于經驗,它發生的概率比較大。一旦指出,這種關系似乎就變得很明顯了,但概率推理的關鍵在于仔細思考如何解釋數據、形成假設并改變你自己的信念,即使面對的是一個普通的日常場景。如果沒有假設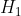 ,那么你就會感到疑惑,因為你無法解釋所觀察到的數據。
,那么你就會感到疑惑,因為你無法解釋所觀察到的數據。
2 收集更多的數據以更新信念
現在你有了數據和假設,然而由于之前你一直對UFO事件持懷疑態度,因此這個假設看起來還是很離譜。為了進一步提高知識水平以得出更可靠的結論,你需要收集更多的數據。這是統計推理的下一個步驟,也是直覺思維的下一個步驟。
為了收集更多的數據,需要進行更多的觀察。具體到UFO這個場景,你需要向窗外看看還能觀察到什么。
當去看外面的亮光時,你注意到這個區域還有更多的燈光,還看到那個巨大的碟形物體用電線吊著,并留意到一個攝像人員。你聽到一聲巨響,有人喊了一聲“停”。
你很有可能會瞬間改變對這個場景中所發生事情的看法。之前,你的推斷是自己可能看到了一個UFO,現在有了一些新數據,你意識到這看起來更像是有人在附近拍電影。
在這一思維過程中,你的大腦又一次瞬間完成了一次復雜的貝葉斯分析!為了更仔細地分析這一事件,下面來分解這一思維過程。
最初,你的假設是:
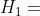 ?有UFO著陸!
?有UFO著陸!
根據你的經驗,這個假設單獨發生的可能性非常小:
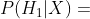 ?非常小
?非常小
這是在現有數據下,你能想到的唯一可能的解釋。但是,當觀察到更多的數據后,你立刻意識到還有一個可能的假設——附近有人正在拍攝電影:
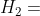 ?有人正在窗外拍攝電影
?有人正在窗外拍攝電影
這個假設單獨發生的概率從直覺上來說也很小(除非你碰巧住在電影制片廠附近):
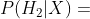 ?很小
?很小
請注意,這里將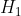 ?的概率設為“非常小”,并將?
?的概率設為“非常小”,并將?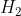 ?的概率設為“很小”。這與我們的直覺相符。假設在沒有任何數據的情況下有人走過來詢問:“你認為哪一種可能性更大——是UFO夜間出現在你家附近,還是剛好有電影在你家附近拍攝?”你會回答拍攝電影的可能性要比出現UFO的可能性更大。
?的概率設為“很小”。這與我們的直覺相符。假設在沒有任何數據的情況下有人走過來詢問:“你認為哪一種可能性更大——是UFO夜間出現在你家附近,還是剛好有電影在你家附近拍攝?”你會回答拍攝電影的可能性要比出現UFO的可能性更大。
當改變信念時,我們需要用一種方法將新得到的數據考慮進去。
3 對比假設
最開始,盡管不太相信,但你接受了出現UFO的假設,因為除此之外你想不出任何其他解釋。然而現在出現了另一種可能的解釋——正在拍攝電影,由此產生了備擇假設(alternative hypothesis)。思考備擇假設的過程,就是利用你所掌握的數據對多種假設進行比較的過程。
當看到電線、電影攝制組和額外的燈光時,你所掌握的數據就發生了變化。更新后的數據是:
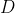 更新后?
更新后? ?亮光, 碟形物體, 電線, 攝制組, 其他燈光等
?亮光, 碟形物體, 電線, 攝制組, 其他燈光等
在觀察到這些額外的數據后,你改變了對所發生事情的結論。下面將這個過程分解成貝葉斯推理過程。第一種假設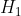 ?給了一種解釋數據的方法,讓你不再困惑;然而隨著觀察的進一步深入,
?給了一種解釋數據的方法,讓你不再困惑;然而隨著觀察的進一步深入,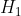 ?已經不能很恰當地解釋數據了。用概率的方法表示就是:
?已經不能很恰當地解釋數據了。用概率的方法表示就是:
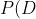 更新后?
更新后?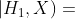 ?非常小
?非常小
現在你有了一種新的假設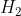 ,它可以更恰當地解釋數據,用概率的方法表示就是:
,它可以更恰當地解釋數據,用概率的方法表示就是:
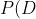 更新后?
更新后?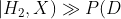 更新后?
更新后?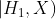
這里的關鍵是,要理解我們是在比較這些假設對觀測數據的解釋程度。當說“在第二種假設中,數據的出現概率要遠遠大于第一種假設”時,我們的意思是,第二種假設可以更恰當地解釋所觀察到的數據。由此,我們就觸及了貝葉斯分析的真正核心:檢驗信念的標準是它們解釋世界的能力。我們說一種信念要比另一種信念更準確,是因為它能更恰當地解釋我們所觀察到的世界。
數學上用這兩種概率的比值來表達這個想法:

當這個比值是一個很大的數時,比如1000,它意味著“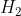 ?對數據的解釋要比?
?對數據的解釋要比?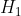 ?恰當1000倍”。因為?
?恰當1000倍”。因為?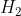 ?對數據的解釋要比?
?對數據的解釋要比?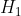 ?好很多,所以我們將信念從?
?好很多,所以我們將信念從?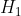 ?改變為?
?改變為?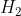 。這正是當你改變對所觀察情況的看法時所發生的事情。現在你之所以相信自己看到的是窗外正在拍攝電影,是因為它更能解釋你所觀察到的所有數據。
。這正是當你改變對所觀察情況的看法時所發生的事情。現在你之所以相信自己看到的是窗外正在拍攝電影,是因為它更能解釋你所觀察到的所有數據。
4 數據影響信念,信念不應該影響數據
最后值得強調的一點是,所有這些示例中唯一不變的是數據。你的假設可以改變,你在這個世界上的經驗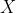 ?也可以與別人不同,但是數據?
?也可以與別人不同,但是數據?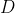 ?則是所有人共享的。
?則是所有人共享的。
思考下面這兩個公式。第一個已經在本章中多次使用:
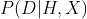
它可以理解為“根據給定的假設和我的經驗所得出的數據概率”,或者更直白地說,“我的信念對所觀察到的數據解釋得如何”。
但在日常思維中,有一種反過來的情況,那就是:
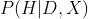
它可以理解為“根據數據和在這個世界上的經驗,我的信念的概率”,或者“我觀察到的情況對我的信念的支持程度”。
在第一種情況下,我們會根據所收集到的數據和對世界的觀察來改變自己的信念,從而更恰當地描述這個世界。在第二種情況下,我們收集數據來支持自己當前的信念。貝葉斯思維就是改變你的想法,更新你對世界的理解。我們觀察到的數據都是真實的,所以我們的信念終歸需要轉變,直到與數據一致。
在生活中,你的信念也應該是始終可變的。
當攝制組收工時,你注意到所有的面包車上都有同一個徽章圖案。你隱約聽到有人說:“嗯,這應該騙過了所有看到這一場景的人……真是好主意。”
有了這些新數據后,你的信念可能會再次改變!
5 小結
下面來回顧一下本章所介紹的內容。你根據現有的經驗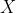 ?形成了最初的信念。而觀察到的數據?
?形成了最初的信念。而觀察到的數據?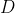 ,要么與你的經驗一致,即?
,要么與你的經驗一致,即?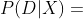 ?很大;要么讓你感到驚訝,即?
?很大;要么讓你感到驚訝,即?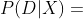 ?很小。為了理解這個世界,你信賴根據觀察所形成的信念,或者說假設?
?很小。為了理解這個世界,你信賴根據觀察所形成的信念,或者說假設? 。很多時候,一種新的假設可以解釋讓你感到驚訝的數據,用概率的語言表示就是?
。很多時候,一種新的假設可以解釋讓你感到驚訝的數據,用概率的語言表示就是?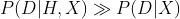 。當收集到新的數據或產生新的想法時,你可以形成更多的假設,如?
。當收集到新的數據或產生新的想法時,你可以形成更多的假設,如?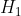 、
、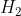 、
、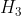 ?等。當一種新的假設要比舊的假設更能解釋收集到的數據時,即當出現下面這種情況時,你會改變自己的信念。
?等。當一種新的假設要比舊的假設更能解釋收集到的數據時,即當出現下面這種情況時,你會改變自己的信念。
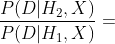 ?較大數值
?較大數值
最后,你應該更關注那些改變你的信念的數據,而不是確保數據支持你的信念,即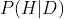 ?的值。
?的值。
有了這些基礎,就可以往其中添加數值了。你將用數學方法模擬自己的信念,從而精確地決定你應該如何以及何時改變自己的信念。
6 練習
試著回答以下問題,檢驗一下你對貝葉斯推理的理解程度。
(1) 使用本章介紹的數學符號,將下列表述改寫為數學表達式:
下雨的概率較小;
在陰天,下雨的概率較大;
下雨時,你帶傘的概率要遠遠大于通常情況下帶傘的概率。
(2) 使用本章介紹的方法,將你在下述場景中觀察到的數據整理為數學表達式,然后提出假設來解釋這些數據。
你下班回到家,看到正門是開著的且側窗壞了。走進門后,你很快發現自己的筆記本計算機不見了。
(3) 下述場景在第2題的基礎上增加了一些數據。使用本章介紹的數學符號演示這些新信息如何改變你的信念,并提出第2個假設來解釋這些數據。
鄰居家的孩子跑過來向你道歉,他不小心將石頭扔到你家的窗戶上,打碎了玻璃。同時他還說,他看見了你的筆記本計算機,因為不想讓它被偷,所以他打開正門將它拿回了家。現在你的筆記本計算機在他家,很安全。
編輯:黃飛
-
貝葉斯
+關注
關注
0文章
77瀏覽量
12763
原文標題:強大的貝葉斯定理,看完后忍不住驚嘆數學太重要了!
文章出處:【微信號:vision263com,微信公眾號:新機器視覺】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
基于貝葉斯網絡的軟件項目風險評估模型
貝葉斯IP網絡擁塞鏈路推理
如何理解貝葉斯公式
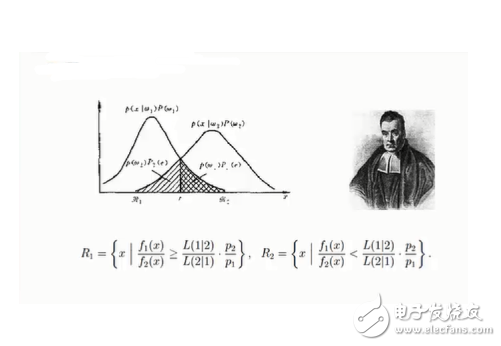





 關于貝葉斯概念進行形式化的建模和推理
關于貝葉斯概念進行形式化的建模和推理












評論