亥姆霍茲定理內(nèi)容及其意義 簡述亥姆霍茲定理及其意義
亥姆霍茲定理(Helmholtz's theorem)是物理力學(xué)中的一個重要定理,它被廣泛應(yīng)用于液體力學(xué)、電磁學(xué)、熱力學(xué)等領(lǐng)域。該定理是由德國科學(xué)家赫爾曼·馮·亥姆霍茲(Hermann von Helmholtz)在19世紀提出的。
亥姆霍茲定理分為兩個部分,即“法向分量”與“切向分量”,下面將詳細介紹它們的內(nèi)容與意義。
一、法向分量
在數(shù)學(xué)上,亥姆霍茲定理的“法向分量”又稱為散度定理(the divergence theorem)。該定理描述了一個有限多面體(finite polyhedron)的表面積分等于該多面體內(nèi)部的體積分的散度。換言之,對于一個向量場(vector field)V,其在有限多面體Ω的表面的通量(flux)等于V在Ω內(nèi)的散度的體積積分(volume integral)。
這個定理可以用數(shù)學(xué)公式表示為:
$\int\int_{S}\vec{V}·\vec{n}dS=\int\int\int_{\Omega}\nabla\cdot \vec{V}dv$
其中,S為有限多面體Ω的表面,$\vec{V}$為向量場,$\vec{n}$為S上任意一點的法向量(outward normal),$dS$為該點的面積元素,$\nabla\cdot\vec{V}$為V的散度,$dv$為Ω內(nèi)任意一點的體積元素。
利用散度定理可以將表面積分(surface integral)轉(zhuǎn)化為體積積分(volume integral),從而簡化研究向量場在有限多面體Ω內(nèi)的問題。
在物理學(xué)中,散度定理可以用于描述液體或氣體的質(zhì)量流量、電場的電通量、流體的質(zhì)量守恒等。例如,在流體力學(xué)中,利用散度定理可以將流體質(zhì)量的入口和出口流量之差等價于質(zhì)量通過管道端點的散度。通過求解內(nèi)部的散度可以推斷出管道內(nèi)部的流量狀態(tài)。
二、切向分量
亥姆霍茲定理的另一部分是切向分量(the curl theorem on continous fields),也稱作旋度定理(the curl theorem)。該定理描述了一個矢量場在一個閉合曲面的切向通量與該矢量場在該曲面所圍成的區(qū)域上的環(huán)向積分的關(guān)系。也就是說,切向分量可以將矢量場的旋度與環(huán)向積分相聯(lián)系。
具體來說,對于一個矢量場$\vec{V}$以及一個由C圍成的有向閉合曲線,矢量場在該曲線內(nèi)的環(huán)向積分等于該曲線的切向量上的旋度對應(yīng)的通量。
該定理可以用數(shù)學(xué)公式表示為:
$\oint_{C}\vec{V}\cdot\vec{t}dl=\int\int_{S}\nabla\times \vec{V}\cdot\vec{n}dS$
其中,$\vec{t}$為C上任意一點的切向量(tangent vector),$dl$為該點的長度元素,$\vec{n}$為S上任意一點的法向量,$\nabla\times\vec{V}$為V的旋度。
切向分量可以用于研究電磁場中的電磁感應(yīng)、磁力對物體的影響、天氣的形成與變化等問題。例如,利用旋度定理可以得到磁通量變化所產(chǎn)生的渦旋電場的方向。這項成果有助于我們理解電磁感應(yīng)現(xiàn)象,從而為磁場控制和電流生成等工作提供理論基礎(chǔ)。
三、亥姆霍茲定理的意義
亥姆霍茲定理在物理學(xué)、天文學(xué)等領(lǐng)域中被廣泛應(yīng)用。它的主要意義有以下三個方面:
1、亥姆霍茲定理為衡量和研究物體內(nèi)部物理量提供了一種可靠的方法。利用定理中的體積積分和表面積分可以準確計算物體內(nèi)部的質(zhì)量、能量、電流等物理量。
2、亥姆霍茲定理是一種常用的求解物理量方程的工具。通過使用散度定理和旋度定理,可以將各種物理量的宏觀效應(yīng)歸結(jié)為局部的微觀變化,從而為求解宏觀物理量方程提供方法。
3、亥姆霍茲定理可以促進各領(lǐng)域間的交叉應(yīng)用。由于散度定理和旋度定理適用于各種不同的場,因此它們可以將不同領(lǐng)域的物理量聯(lián)系起來。這項成果有助于促進物理學(xué)、天文學(xué)、流體力學(xué)等領(lǐng)域的合作。
-
亥姆霍茲
+關(guān)注
關(guān)注
0文章
35瀏覽量
407
發(fā)布評論請先 登錄
微型裝置以獨特方式捕獲并測量光
SMA連接器全稱及其意義

亥步多模態(tài)醫(yī)療大模型發(fā)布:人工智能引領(lǐng)醫(yī)療新紀元
歐姆定律和基爾霍夫定律的區(qū)別
CAP 定理:理論、實踐
負電荷受洛倫茲力的方向怎么判斷
疊加定理時受控源怎么處理
疊加定理電壓源和電流源怎么處理
如何在疊加定理中實現(xiàn)電源電壓為零
疊加定理電壓源短路的處理
疊加定理電壓源單獨作用時電流源代表什么
戴維南和諾頓定理的適用條件
戴維南和諾頓定理的應(yīng)用場合
戴維南和諾頓定理適用于什么電路
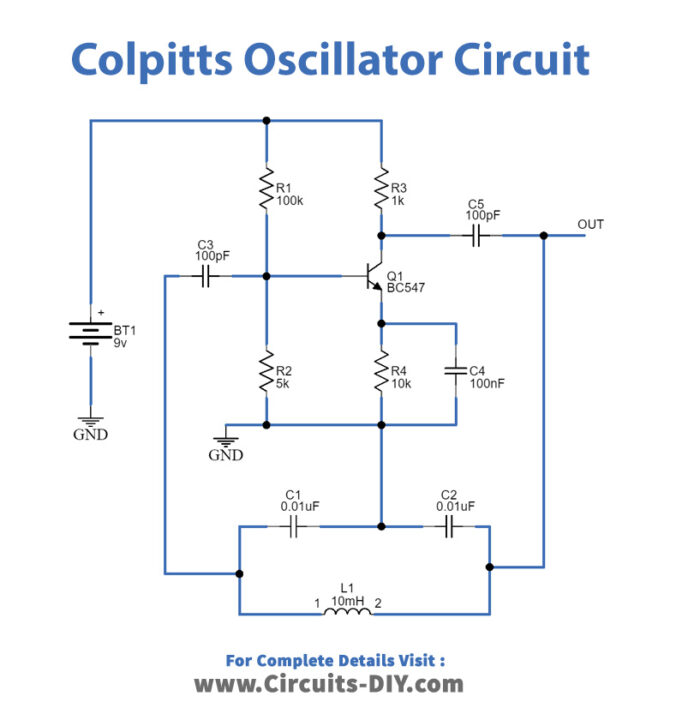
考畢茲振蕩器電路圖 考畢茲振蕩器的工作原理和特點





 亥姆霍茲定理內(nèi)容及其意義 簡述亥姆霍茲定理及其意義
亥姆霍茲定理內(nèi)容及其意義 簡述亥姆霍茲定理及其意義










評論