亥姆霍茲定理的內容和意義
亥姆霍茲定理,又稱為亥姆霍茲分解定理或向量分解定理,是矢量解析學中的一項重要定理,它描述了矢量場可以分解為兩個旋度和散度互不影響的部分。此定理是由赫爾曼·馮·亥姆霍茲于1858年提出,至今已成為了矢量分析和場論研究的基礎性理論之一。
亥姆霍茲定理的內容是指出任何三維向量場都可以分解為旋度場和散度場的和,即:
$\vec{A} = -\nabla \Phi + \nabla \times \vec{B}$
其中,$\vec{A}$ 為原向量場,$\Phi$ 為散度場,$\vec{B}$ 為旋度場,$\nabla$ 為梯度運算符,$\times$ 為向量積運算符。這個公式表明了一個重要的事實,即一個任意的向量場不僅包含了旋度和散度兩種性質,而且它們之間還存在著一種被稱為“互補”的關系。
具體來說,$\Phi$ 表示原向量場在每個點上的散度值,也就是流入或流出該點的矢量量。散度可以理解為矢量場的“源”或者“匯”,如果一個場的散度在某個位置非零,則意味著該位置上有一些物質在進入或者離開該點。例如,一個熱源會在它周圍產生一個具有正的散度值的溫度場,因為從它處產生的熱量會向四周擴散,導致溫度場的散度值逐漸減小。
$\vec{B}$ 表示原向量場在每個點上的旋度值,也就是該點周圍的環流效應。旋度可以理解為矢量場的“渦旋”或者“回旋”,如果一個場的旋度在某個位置非零,則意味著該位置上存在一些旋轉的流體或物質。例如,一個氣旋會在其中心產生一個具有正的旋度值的氣旋場,因為在該中心處的空氣會旋轉而產生渦旋流動。
可以看出,散度和旋度是描述了矢量場內部物質或者物理量的傳遞和流動方式。而一個向量場的旋度與散度相互獨立,也就是說它們可以分別得到,互相不影響。因此,如果要對一個任意的向量場進行分析,我們可以首先通過求得其散度和旋度來分別研究它內部的質量和能量的運動方式。
另外,亥姆霍茲定理的意義還在于,它為我們提供了一種矢量場的分解方法。通過對原向量場進行分解,我們可以更加深入地了解矢量場內部的結構和物理規律。例如,在電磁學中,可以將電場 $\vec{E}$ 和磁場 $\vec{H}$ 進行亥姆霍茲分解,得到電勢 $\Phi$ 和矢勢 $\vec{A}$,這些分解量對于電磁現象的模擬和計算十分重要。
此外,亥姆霍茲定理還在數學和物理學中具有廣泛的應用。比如,在流體力學中,可以將流體速度場按照亥姆霍茲定理進行分解,得到每個點周圍的旋度和散度值,這可以幫助研究流體流動的本質和規律;在偏微分方程的研究中,亥姆霍茲定理可以用來證明一些基本性質和特殊解形式的存在性;在計算機圖像領域,亥姆霍茲分解可以用來優化圖像處理算法,提高圖像的清晰度和準確度等等。
總之,亥姆霍茲定理是矢量分析中的一項基本定理,它描述了矢量場可以分解為兩個旋度和散度互不影響的部分,為我們深入研究物理規律提供了一種通用的分析手段。此外,亥姆霍茲定理在物理學、數學和工程學等領域中都有著廣泛的應用,具有重要的理論和實際意義。
-
計算機
+關注
關注
19文章
7626瀏覽量
90135 -
亥姆霍茲
+關注
關注
0文章
35瀏覽量
406
發布評論請先 登錄
微型裝置以獨特方式捕獲并測量光
泰雷茲發布數據風險智能解決方案
亥步多模態醫療大模型發布:人工智能引領醫療新紀元
歐姆定律和基爾霍夫定律的區別
CAP 定理:理論、實踐
負電荷受洛倫茲力的方向怎么判斷
疊加定理時受控源怎么處理
疊加定理電壓源和電流源怎么處理
如何在疊加定理中實現電源電壓為零
疊加定理電壓源短路的處理
疊加定理電壓源單獨作用時電流源代表什么
戴維南和諾頓定理的適用條件
戴維南和諾頓定理的應用場合
戴維南和諾頓定理適用于什么電路
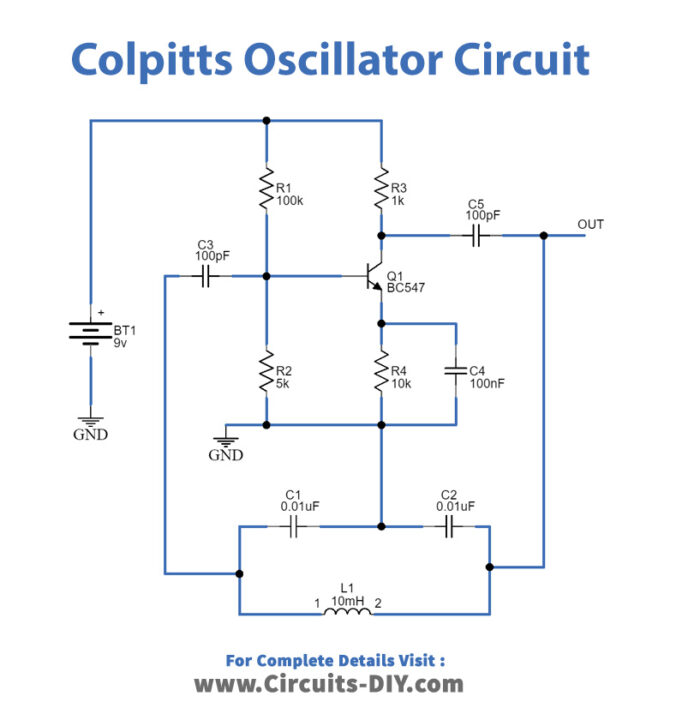
考畢茲振蕩器電路圖 考畢茲振蕩器的工作原理和特點





 亥姆霍茲定理的內容和意義
亥姆霍茲定理的內容和意義










評論