2.1 歐拉定理
歐拉定理是剛體定點轉(zhuǎn)動理論中的一個重要定理,它表明剛體繞固定點的任何位移都可以通過繞通過此點的某一軸轉(zhuǎn)過一個角度來實現(xiàn)。在單位時間間隔Δt內(nèi),假設(shè)剛體的角速度為ω,則該轉(zhuǎn)動軸的方向e及繞該軸轉(zhuǎn)過的角度φ分別為:e = ω/|ω|,φ = |ω|Δt。
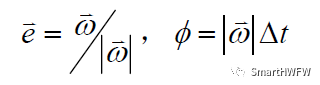
相應(yīng)四元數(shù)表示式為:
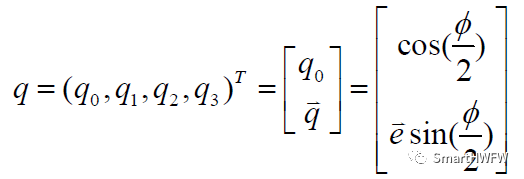
滿足約束條件
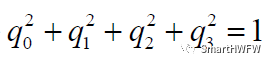
以超復(fù)數(shù)形式表示有:
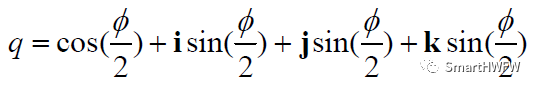
滿足約束條件
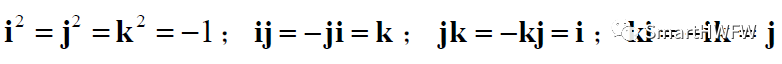
利用三角公式:
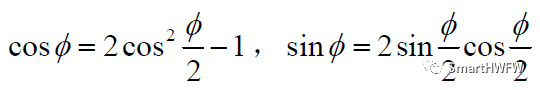
可將四元數(shù)轉(zhuǎn)化成姿態(tài)矩陣 b系到R系
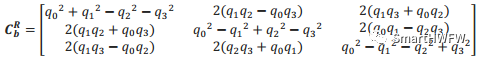
可將四元數(shù)轉(zhuǎn)化成姿態(tài)矩陣 R系到b系
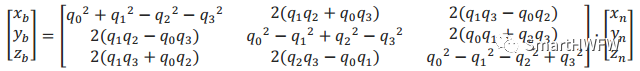
Tips:R系是一種用于描述空間中點位置的導(dǎo)航坐標(biāo)系,其中的坐標(biāo)值表示相對于地球的位置。b系是一種用于描述載體(例如航空器、船舶等)位置的坐標(biāo)系,其中的坐標(biāo)值表示相對于載體的位置。
3. Matlabe四元數(shù)轉(zhuǎn)方向余弦矩陣
API
function[y1,...,yN]=myfun(x1,...,xM)聲明名為myfun的函數(shù),該函數(shù)接受輸入x1,...,xM并返回輸出y1,...,yN
q2mat(),qua2dcm(),quat2dcm()將四元數(shù)轉(zhuǎn)換矩陣
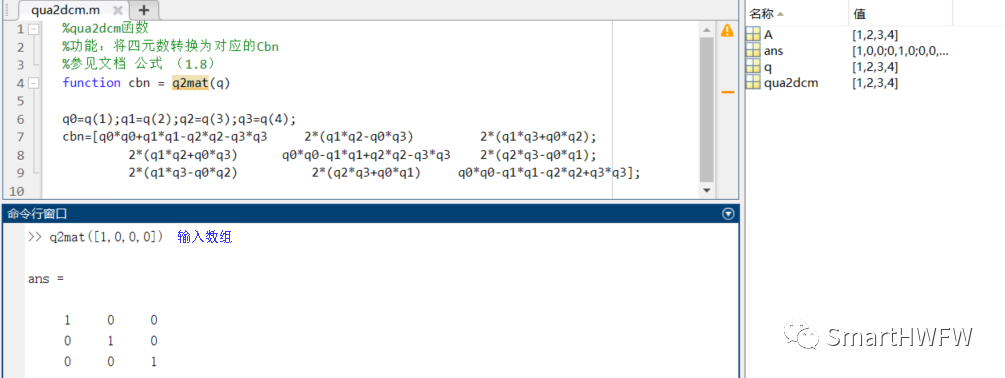
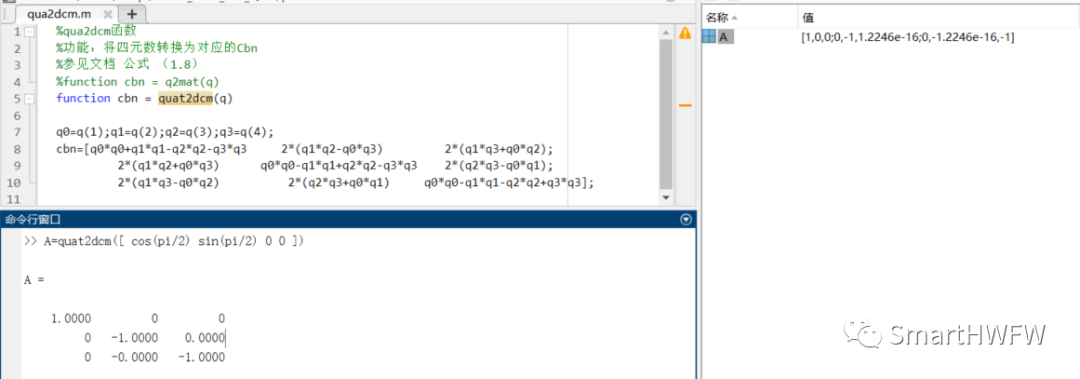
4.C語言實現(xiàn)四元數(shù)轉(zhuǎn)方向余弦矩陣
基于 QMI8658 姿態(tài)傳感器實現(xiàn)四元數(shù)轉(zhuǎn)換為方向余弦矩陣的過程如下:
STEP1: 根據(jù)傳感器獲取到的四元數(shù)數(shù)據(jù),我們可以得到四元數(shù)的四個分量:q0、q1、q2、q3。
STEP2: 我們可以根據(jù)四元數(shù)的定義,將其轉(zhuǎn)換為方向余弦矩陣。具體的轉(zhuǎn)換公式如下:
| C11 C12 C13 | | C21 C22 C23 | | C31 C32 C33 | 其中,C11、C12、C13、C21、C22、C23、C31、C32、C33 分別表示方向余弦矩陣的九個元素。
STEP3: 我們可以通過串口將獲取到的四元數(shù)和方向余弦矩陣輸出。
以下是基于 QMI8658 姿態(tài)傳感器獲取到的靜止放置在水平面,Z軸向上的四元數(shù)和方向余弦矩陣數(shù)據(jù):
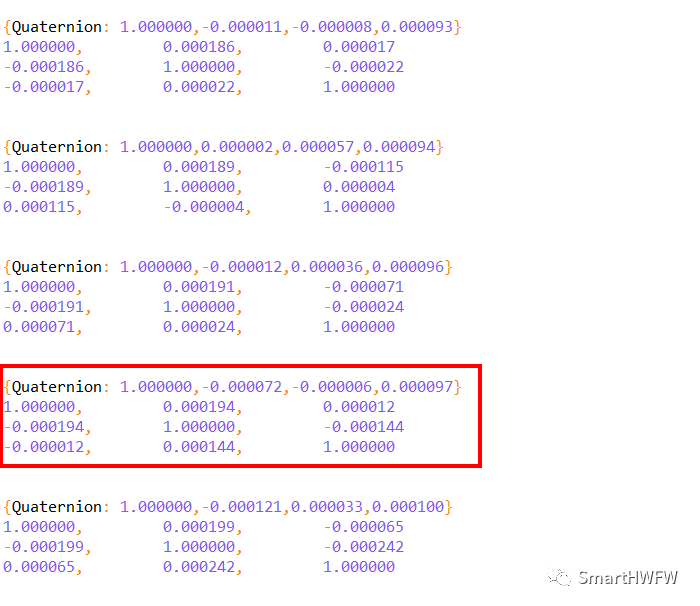
我可以使用Wolfram Alpha計算器進行計算和校驗,并給出結(jié)果。
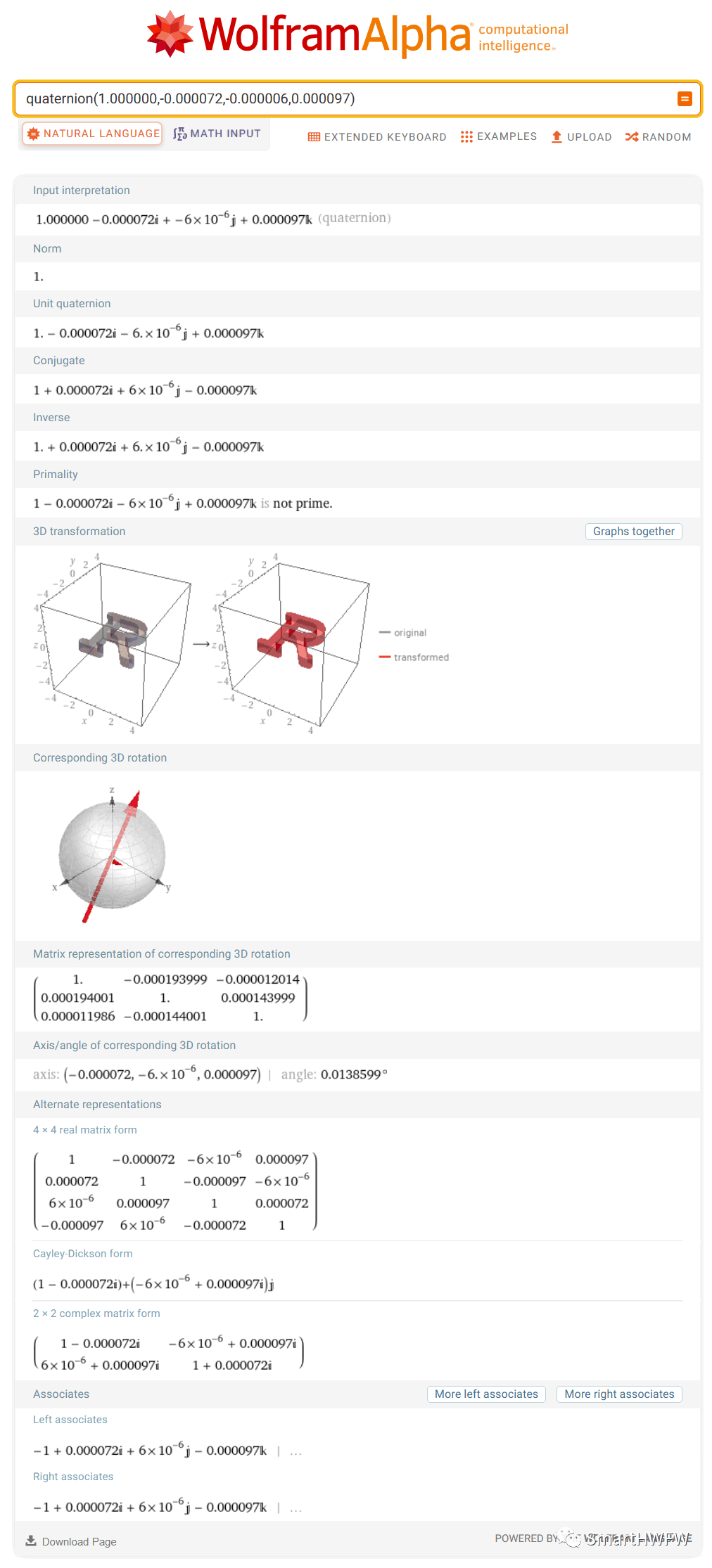
審核編輯:劉清
-
傳感器
+關(guān)注
關(guān)注
2562文章
52524瀏覽量
763472 -
計算器
+關(guān)注
關(guān)注
16文章
439瀏覽量
37917
原文標(biāo)題:MEMS_慣性傳感器程序集01-四元數(shù)轉(zhuǎn)方向余弦矩陣
文章出處:【微信號:SmartHWFW,微信公眾號:SmartHWFW】歡迎添加關(guān)注!文章轉(zhuǎn)載請注明出處。
發(fā)布評論請先 登錄
四元數(shù),卡爾曼資料
經(jīng)典干貨:無人機四元數(shù)解算姿態(tài)角解析
四元數(shù)更新算法問題
請問我用四元數(shù)轉(zhuǎn)歐拉角造成的這些問題該怎么解決?
【案例分享】四軸飛行器6050六軸傳感器軟件姿態(tài)解算
四元數(shù)飛控示意附圖
姿態(tài)解算需要頻繁組合旋轉(zhuǎn)和用旋轉(zhuǎn)變換向量
請問MotionFX庫中的四元數(shù)是如何排序的?
旋轉(zhuǎn)矩陣、四元數(shù)、歐拉角比較
采用余弦相似度的習(xí)俗非負(fù)矩陣分解算法
MPU6050的四元數(shù)解算姿態(tài)方法

C語言實現(xiàn)歐拉角轉(zhuǎn)四元數(shù)
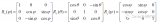
MSP430F5xx系列上使用方向余弦矩陣算法的九軸傳感器融合






 四元數(shù)轉(zhuǎn)方向余弦矩陣介紹
四元數(shù)轉(zhuǎn)方向余弦矩陣介紹










評論