主要是介紹如何對spmv算法進行優化。Spmv,即稀疏化的矩陣向量乘操作,關于稠密的矩陣向量乘操作,已經在上一篇文章中介紹過了。關于稀疏kernel的優化,是CUDA優化中最難的一部分,其難度在于稀疏特性千差萬別,需要針對不同的應用、不同的數據選擇不同的數據存儲格式,然后再根據不同的數據特點進行特定的并行算法設計。而現實生活中,尤其是科學計算里面,基本上都是稀疏問題。在深度學習領域中,也一直有針對稀疏模型的研究,主要是針對推理方向,將模型進行剪枝之后,直接減少了計算量來達到對模型的加速目的。但實際上,為了保證模型的精度,稀疏度有限,且稀疏問題很難充分地利用硬件性能,導致了這一條路線其實并不好走。嘮嘮叨叨說了挺多,總之,稀疏kernel的優化是一個非常難的話題。本文會詳細地介紹一下spmv。
一、前言
在說spmv之前,說一下稀疏格式。當矩陣中的絕大多數元素都是0時,需要一些特殊的格式來存儲非零元素。這些格式也就是稀疏格式,常用的稀疏格式有:COO、CSR、DIA、ELL、HYB。深度學習領域還有blocked CSR、blocked ELL等。具體的稀疏格式總結見以下鏈接:
稀疏矩陣存儲格式總結+存儲效率對比:COO,CSR,DIA,ELL,HYB - Bin的專欄 - 博客園www.cnblogs.com/xbinworld/p/4273506.html
在本文中,使用CSR格式存儲稀疏矩陣,后續所說的一系列優化也是針對CSR格式而言。說完了稀疏格式,現在再來說一下spmv,即稀疏矩陣向量乘。稠密的矩陣向量乘,即gemv已經在之前說過了。具體的操作即給定稀疏矩陣A和向量x,需要計算兩者的乘積y。示意圖如下。
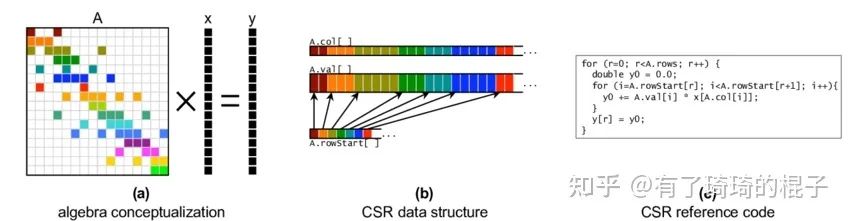
spmv介紹
二、并行算法設計
并行算法設計,主要是block和thread的設計,在這里主要參考了cusp的實現。有一個很重要的考慮是workload的分配。我們需要使用多少個線程來負責A矩陣中一行的計算?需要說明的是,在不同的數據特性下,需要采用不同的取值。如果這一行的元素非常多,那使用一個warp或者一個block,如果這一行只有一個元素,只需要一次乘加指令,那顯然只能使用一個線程,畢竟用兩個線程處理一個元素,怎么都不像正常人能干出的事。因而,我們假定一個參數,即THREADS_PER_VECTOR,來代表這個值。每THREADS_PER_VECTOR個線程為一組,他們需要負責A矩陣中一行元素的計算。
說完了這個核心思路,接下來看看每個線程需要干的工作。每個線程都要單獨地對A矩陣的offset和index等進行讀取,然后計算當前行的結果。如果每一行的元素特別少,比如這一行元素有4個,THREADS_PER_VECTOR就設為4,有8個元素就設為8,平均多少個元素,THREADS_PER_VECTOR就設為幾,但上限是32。元素比32多的話,就多進行幾個迭代即可。總之最多使用一個warp來處理一行元素。
至于如何得到一行元素有多少,row_offset數組長度除以y數組長度即可得。有必要在這里再提一句的是,這些參數的選擇,以及對于不均衡的A矩陣元素如何處理,這些都是比較棘手的問題。有一大堆的論文在談負載均衡和自動調參這兩個事情,大家可以搜一下相關的論文瞅瞅。
講完了思路,下面說一下具體的代碼,如下:
template__device__ __forceinline__ float warpReduceSum(float sum) { if (WarpSize >= 32)sum += __shfl_down_sync(0xffffffff, sum, 16); // 0-16, 1-17, 2-18, etc. if (WarpSize >= 16)sum += __shfl_down_sync(0xffffffff, sum, 8);// 0-8, 1-9, 2-10, etc. if (WarpSize >= 8)sum += __shfl_down_sync(0xffffffff, sum, 4);// 0-4, 1-5, 2-6, etc. if (WarpSize >= 4)sum += __shfl_down_sync(0xffffffff, sum, 2);// 0-2, 1-3, 4-6, 5-7, etc. if (WarpSize >= 2)sum += __shfl_down_sync(0xffffffff, sum, 1);// 0-1, 2-3, 4-5, etc. return sum; } template __global__ void My_spmv_csr_kernel(const IndexType row_num, const IndexType * A_row_offset, const IndexType * A_col_index, const ValueType * A_value, const ValueType * x, ValueType * y) { const IndexType THREADS_PER_BLOCK = VECTORS_PER_BLOCK * THREADS_PER_VECTOR; const IndexType thread_id = THREADS_PER_BLOCK * blockIdx.x + threadIdx.x; // global thread index const IndexType thread_lane = threadIdx.x & (THREADS_PER_VECTOR - 1); // thread index within the vector const IndexType row_id = thread_id / THREADS_PER_VECTOR; // global vector index if(row_id < row_num){ const IndexType row_start = A_row_offset[row_id]; //same as: row_start = Ap[row]; const IndexType row_end = A_row_offset[row_id+1]; // initialize local sum ValueType sum = 0; // accumulate local sums for(IndexType jj = row_start + thread_lane; jj < row_end; jj += THREADS_PER_VECTOR) sum += A_value[jj] * x[ A_col_index[jj] ]; sum = warpReduceSum (sum); if (thread_lane == 0){ y[row_id] = sum; } } }
首先說一下傳入的幾個模板參數,IndexType代表索引類型,一般用int,如果矩陣十分巨大,可以考慮long long,ValueType代表數值存儲的格式,科學計算一般都雙精度,深度學習一般用單精度,或者fp16。推理甚至有一些int8這樣的需求。THREADS_PER_VECTOR這個參數已經在前面說過了,VECTORS_PER_BLOCK則是代表一個block中有多少vector。我們盡可能地保證一個block有256個線程,所以VECTORS_PER_BLOCK = 256 / THREADS_PER_VECTOR。看完了模板參數,再看函數輸入參數,分別是A矩陣的行數,A矩陣的CSR表示,有3個數組,然后是向量x和向量y。
接下來到了具體的kernel邏輯,首先計算了四個參數,需要注意的是thread_lane和row_id參數,thread_lane代表當前元素是當前組里面的第幾個元素,row_id代表當前元素負責A矩陣中第幾行的計算。接下來的邏輯也比較明了,先計算當前行對應的索引值,即row_start和row_end。定義sum變量來存儲該行的計算結果,而后進行多次迭代,將每個線程對應的sum取出來,最后將sum元素進行warp的reduce_sum操作。最后將元素寫到y向量中。
三、優化技巧
在上一節中已經把代碼說完了,接下來盤點一下具體的優化技巧,以及優化中需要考慮的方方面面。
1、合理的block和thread調整。我一直覺得這個點是優化中最重要的一點。核心就是THREADS_PER_VECTOR需要根據實際的數據進行調整。這一點主要是考慮到如果使用更多的線程處理的話,只有THREADS_PER_VECTOR個線程在工作,其他的線程都被浪費了。
2、Shuffle指令減少訪存的latency。在不使用shuffle指令的話,只能通過shared memory完成最后的求和操作。從shared memory中取數比寄存器之間直接訪問要花費更多的latency。因而要盡可能地使用shuffle指令。
3、對于global memory的合并訪存。對于稀疏問題,由于CSR格式中的col數組和val數組不能保證地址對齊,因而針對global memory的合并訪存其實是有一定的困難。我們可以仔細地來進行分析。當A矩陣行數比較多的情況下,spmv主要的訪存有3部分,分別是A_value,A_col_index和x。其中,對于A_value和A_col_index的訪存是連續的,但是由于地址不能保證對齊,所以訪存效率大概率不會太高。而對于x的訪存本身就是不連續的,因而cache命中率會顯然易見地低。如何解決這些問題呢?對于A_value和A_col_index的訪存問題,尚可以嘗試對其進行數據填充,強制其地址對齊。而對于x的非連續訪存問題,如何提高訪存效率,這個問題就非常困難了。
4、關于向量化指令的使用。之前在進行gemm和gemv優化中大量地使用了float4這樣的向量化訪存結構。如何將向量化帶到spmv中,這也是一個非常困難的問題。最大的根源是因為每一行的元素不確定,并且本身A中每行的元素就比較少,根本沒有那么多數據去喂到LDS128指令上。
5、關于負載均衡的思考。CUDA上的負載均衡問題可以從兩個角度考慮,一個是block之間的負載均衡,另一個是block/warp內,不同線程之間的負載均衡。關于spmv的負載均衡問題,可以參考一下Speculative Segmented Sum for Sparse Matrix-Vector Multiplication on Heterogeneous Processors。
四、實驗與總結
最后,我們來說一下實驗環節。實驗主要用來說明兩個問題,第一個是THREADS_PER_VECTOR參數對性能的影響,第二個是與cusparse的對比,用以觀察不同數據下的性能表現。
實驗一,從佛羅里達矩陣庫里面選了一個稀疏矩陣,shyy41。平均一行有4.2個元素。我們在不同的參數下進行了實驗,其結果如下:
| THREADS_PER_VECTOR | spmv kernel耗時(ns) |
|---|---|
| 2 | 4093 |
| 4 | 3969 |
| 8 | 4066 |
| 16 | 4368 |
| 32 | 4976 |
這個結果和預期的差不多,因為平均一行元素個數是4.2,所以THREADS_PER_VECTOR參數取4或8會有更好的性能表現。
實驗二,從佛羅里達矩陣庫里面隨機選取了一些矩陣,其稀疏特性如下,矩陣旁邊有x-y-z標識。x和y代表矩陣的行數和列數,z代表矩陣中的非零元個數。
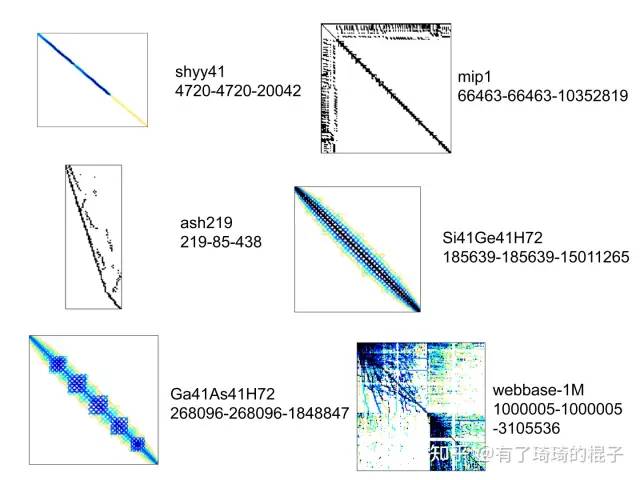
稀疏矩陣
性能表現如下,
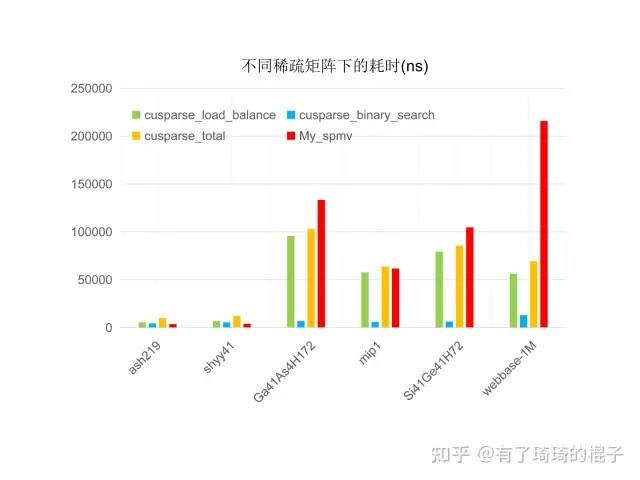
與cusparse的性能對比
結論:
1、先單獨看cusparse的表現,庫里面會調用兩個kernel,分別是binary_seach和load_balance。這個名稱簡寫了。總之,就是cusparse不管來的數據是啥,都會進行負載均衡,在數據量比較多的時候,額外的開銷比較少,能夠取到足夠的效益。
2、如果是結構化的網格,即元素聚集在對角線附近,且每行的非零元都差不了太多的時候,我寫的spmv會比cusparse快一些。如果每行的非零元方差特別大,cusparse中的負載均衡工作就發揮了威力,在web網絡這種矩陣上能夠比我的spmv快2-3倍。總之,在sparse問題中,負載均衡非常重要,我會在下一篇博文中說明如何在spmm中進行負載均衡。
總之,我們實現了spmv kernel,并對主要的優化技巧進行了解析和說明,然后大概地說了一下在spmv上需要注意的問題。通過實驗評估了不同參數對性能的影響以及在不同的稀疏矩陣下同cusparse進行了比較,在部分矩陣上性能能夠超越cusparse。但由于沒有考慮負載均衡,在非均勻網格上,與cusparse有一定的差距。
-
數據
+關注
關注
8文章
7238瀏覽量
90946 -
存儲
+關注
關注
13文章
4497瀏覽量
87040 -
模型
+關注
關注
1文章
3480瀏覽量
49947 -
澎峰科技
+關注
關注
0文章
68瀏覽量
3340
原文標題:深入淺出GPU優化系列:spmv優化
文章出處:【微信號:perfxlab,微信公眾號:perfxlab】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
《MATLAB優化算法案例分析與應用》
多目標優化算法有哪些
如何改進和優化RSA算法
如何優化控制算法的代碼
智能電網定價的光學優化算法
如何使用Spark進行并行FP-Growth算法優化及實現
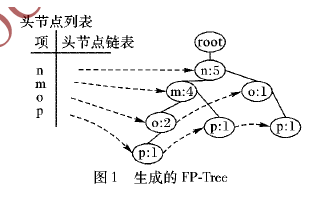
如何進行耦合數據的融合算法的分解優化
如何使用混合果蠅優化算法進行現場服務調度問題的解決方法
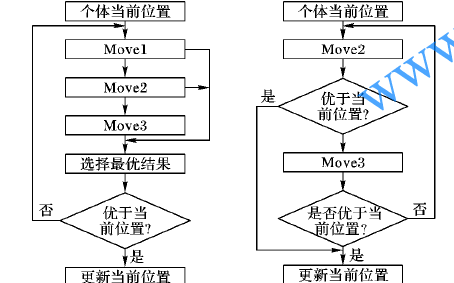





 如何對spmv算法進行優化
如何對spmv算法進行優化










評論