上一篇文章介紹了偶分頻，今天來介紹一下奇數(shù)分頻器的設(shè)計。

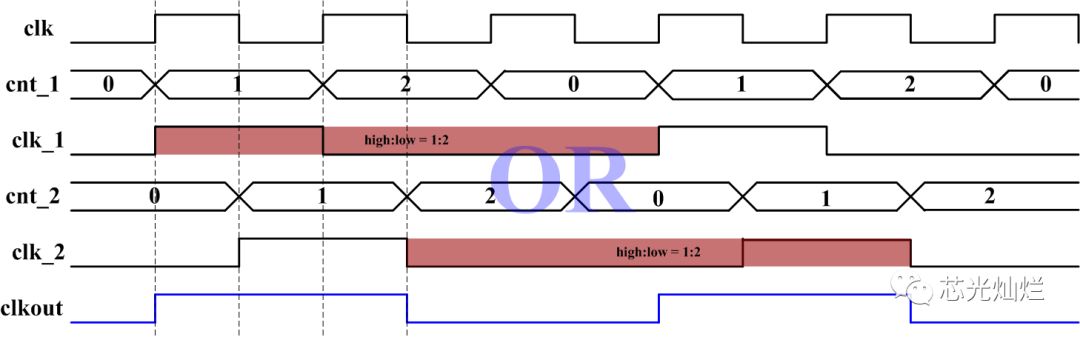
入門從簡單開始，先來個三分頻分析一下。 三分頻其實就是把輸入時鐘的三個周期當作一個周期，具體波形如圖所示。 （本文只針對于占空比為50%的分析）

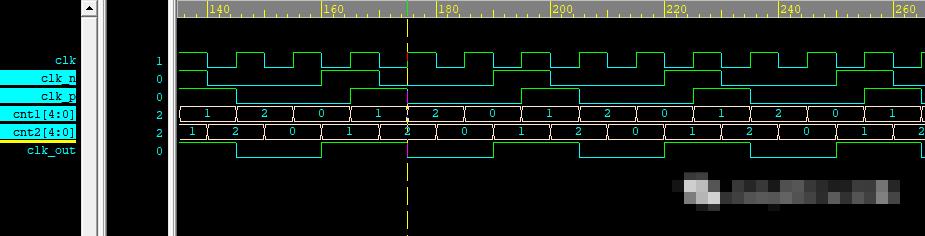
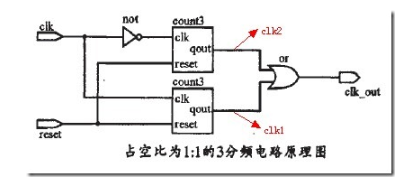
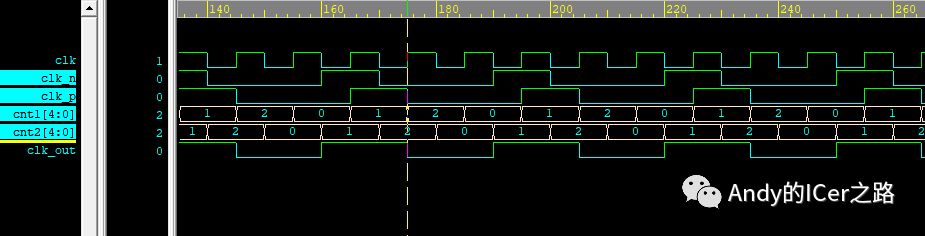
此處還是用計數(shù)器的方式完成設(shè)計，但是與偶分頻有所區(qū)別。 因為奇數(shù)分頻的頻率與輸入的時鐘頻率有相位差，因此需要增加一些信號完成設(shè)計。 clk_n是下降沿觸發(fā)的信號，clk_p是上升沿觸發(fā)的信號，通過計數(shù)并且因為不同的邊沿觸發(fā)而形成一定的相位差，并將兩個信號進行或門處理，最后輸出的就是奇數(shù)分頻結(jié)果了。

缺點分析：奇數(shù)分頻需要在兩個觸發(fā)器之后再加一個組合邏輯門，這個組合邏輯門不僅會增加時鐘的延時，而且在設(shè)計當中可能出現(xiàn)毛刺。

具體的占空比為50%的任意奇數(shù)分頻的代碼如下所示。

`timescale 1ns/1ps
module CLK_DIV #(parameter DIV_NUM=3)(
input clk,
input rst_n,
output clk_out
);

//all odd div
reg [4:0] cnt1,cnt2;
reg clk_p,clk_n;

always @(posedge clk,negedge rst_n)
if(!rst_n) begin
cnt1 <= 0;
clk_p <= 1'b0;
end
else begin
if(cnt1 == DIV_NUM-1) begin
cnt1 <= 0;
clk_p <= clk_p;
end
else begin
cnt1 <= cnt1 + 1'b1;
if(cnt1 == ((DIV_NUM-1)/2)-1 || cnt1 == DIV_NUM-2)
clk_p <= ~clk_p;
end
end

always @(negedge clk,negedge rst_n)
if(!rst_n) begin
cnt2 <= 0;
clk_n <= 1'b0;
end
else begin
if(cnt2 == DIV_NUM-1) begin
cnt2 <= 0;
clk_n <= clk_n;
end
else begin
cnt2 <= cnt2 + 1'b1;
if(cnt2 == ((DIV_NUM-1)/2)-1 || cnt2 == DIV_NUM-2)
clk_n <= ~clk_n;
end
end

assign clk_out = clk_p | clk_n;