整合在一起
現在我們已經完成了消息傳遞、聚合和更新步驟,讓我們把它們放在一起,在單個節點i上形成單個GNN層:
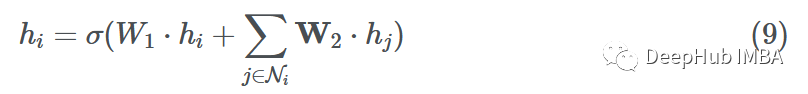
這里我們使用求和聚合和一個簡單的前饋層作為函數F和H。設hi∈Rd, W1,W2?Rd ' ×d其中d '為嵌入維數。
使用鄰接矩陣
到目前為止,我們通過單個節點i的視角觀察了整個GNN正向傳遞,當給定整個鄰接矩陣a和X?RN×d中所有N=∥V∥節點特征時,知道如何實現GNN正向傳遞也很重要。
在 MLP 前向傳遞中,我們想要對特征向量 xi 中的項目進行加權。這可以看作是節點特征向量 xi∈Rd 和參數矩陣 W?Rd′×d 的點積,其中 d′ 是嵌入維度:

如果我們想對數據集中的所有樣本(矢量化)這樣做,我們只需將參數矩陣和特征矩陣相乘,就可以得到轉換后的節點特征(消息):
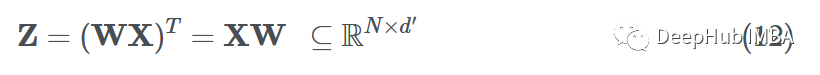
在gnn中,對于每個節點i,消息聚合操作包括獲取相鄰節點特征向量,轉換它們,并將它們相加(在和聚合的情況下)。
單行Ai對于Aij=1的每個指標j,我們知道節點i和j是相連的→eij∈E。例如,如果A2=[1,0,1,1,0],我們知道節點2與節點1、3和4連接。因此,當我們將A2與Z=XW相乘時,我們只考慮列1、3和4,而忽略列2和5:
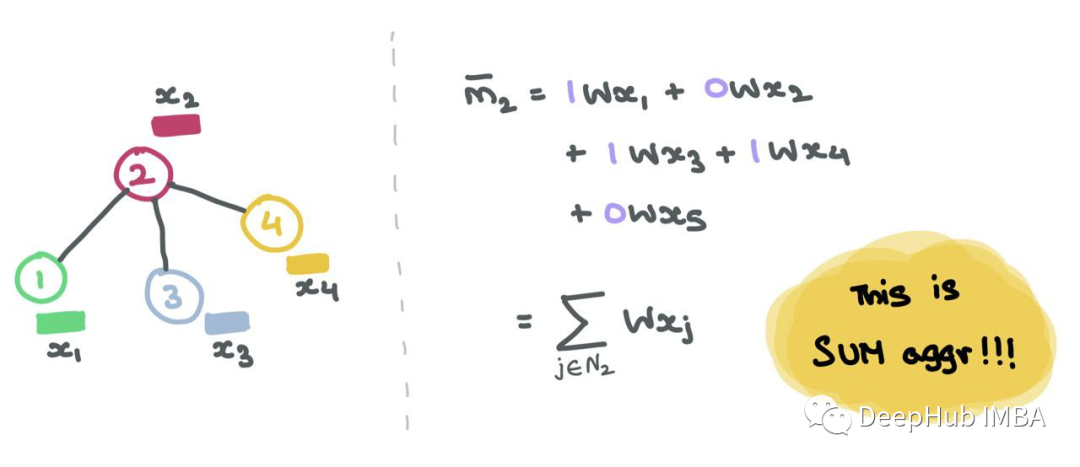
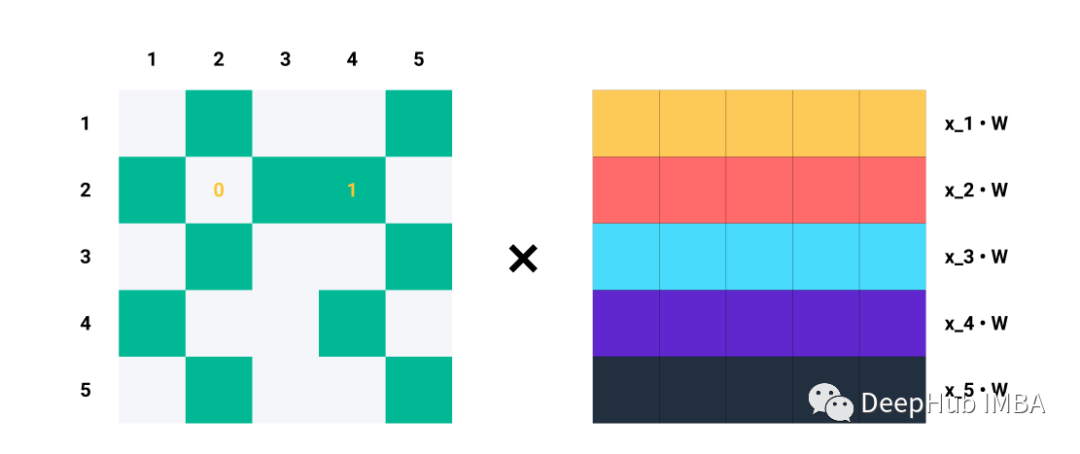
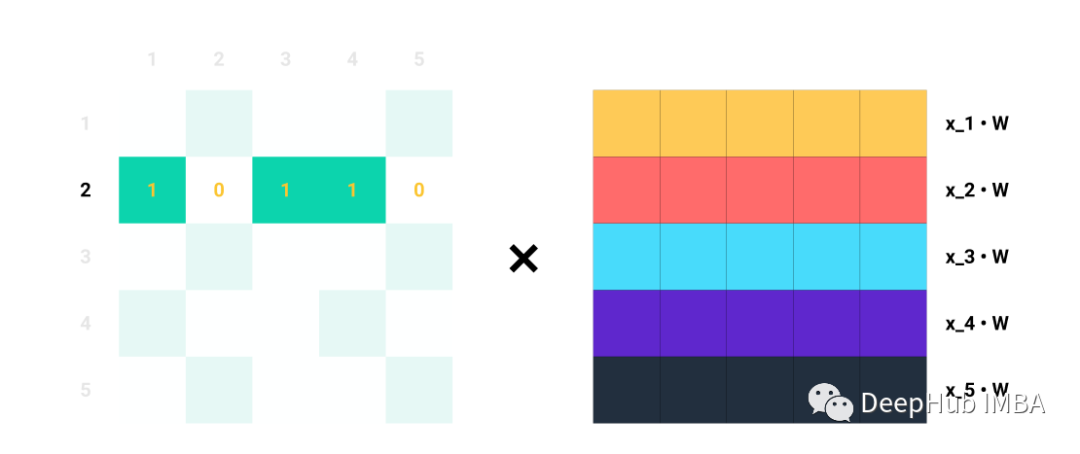
比如說A的第二行。
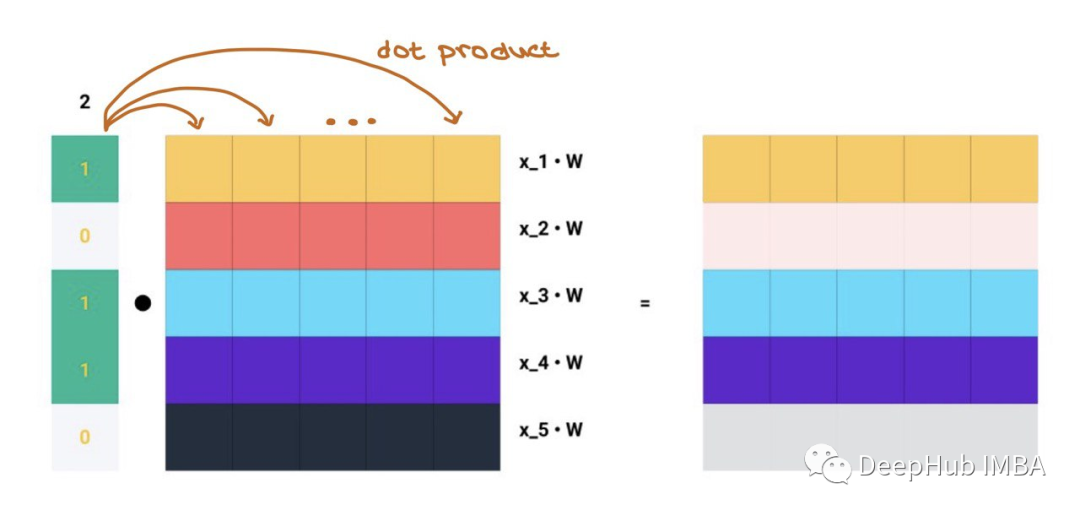
矩陣乘法就是A中的每一行與Z中的每一列的點積,這就是消息聚合的含義!!
獲取所有N的聚合消息,根據圖中節點之間的連接,將整個鄰接矩陣A與轉換后的節點特征進行矩陣乘法:

但是這里有一個小問題:觀察到聚合的消息沒有考慮節點i自己的特征向量(正如我們上面所做的那樣)。所以我們將自循環添加到A(每個節點i連接到自身)。
這意味著對角線的而數值需要進行修改,用一些線性代數,我們可以用單位矩陣來做這個!

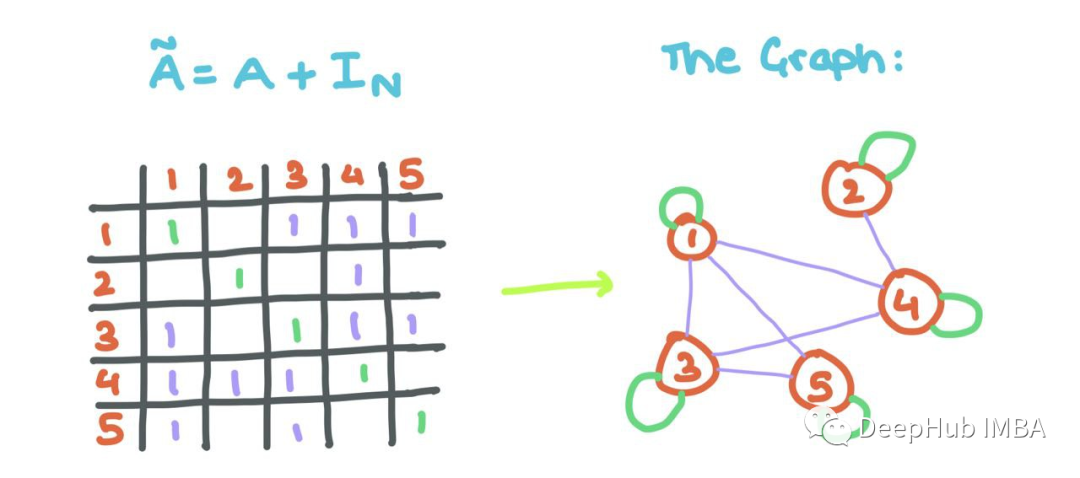
添加自循環可以允許GNN將源節點的特征與其鄰居節點的特征一起聚合!!
有了這些,你就可以用矩陣而不是單節點來實現GNN的傳遞。
?要執行平均值聚合(mean),我們可以簡單地將總和除以1,對于上面的例子,由于A2=[1,0,0,1,1]中有三個1,我們可以將∑j∈N2Wxj除以3,但是用gnn的鄰接矩陣公式來實現最大(max)和最小聚合(min)是不可能的。
GNN層堆疊
上面我們已經介紹了單個GNN層是如何工作的,那么我們如何使用這些層構建整個“網絡”呢?信息如何在層之間流動,GNN如何細化節點(和/或邊)的嵌入/表示?
- 第一個GNN層的輸入是節點特征X?RN×d。輸出是中間節點嵌入H1?RN×d1,其中d1是第一個嵌入維度。H1由h1i: 1→N∈Rd1組成。
- H1是第二層的輸入。下一個輸出是H2?RN×d2,其中d2是第二層的嵌入維度。同理,H2由h2i: 1→N∈Rd2組成。
- 經過幾層之后,在輸出層L,輸出是HL?RN×dL。最后,HL由hLi: 1→N∈RdL構成。
這里的{d1,d2,…,dL}的選擇完全取決于我們,可以看作是GNN的超參數。把這些看作是為MLP層選擇單位(“神經元”的數量)。
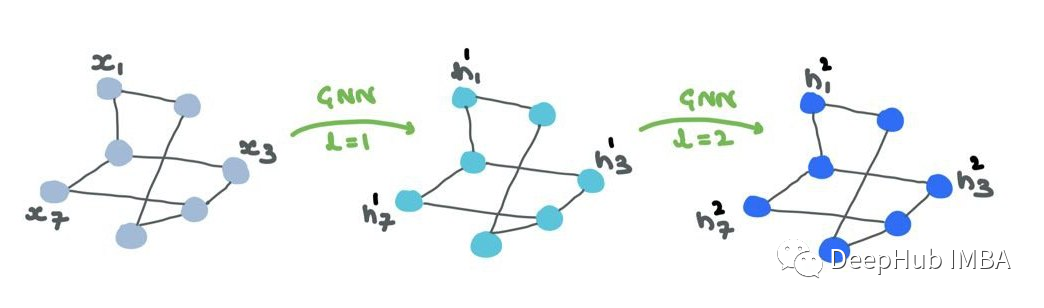
節點特征/嵌入(“表示”)通過GNN傳遞。雖然結構保持不變,但節點表示在各個層中不斷變化。邊表示也將改變,但不會改變連接或方向。
HL也可以做一些事情:
我們可以沿著第一個軸(即∑Nk=1hLk)將其相加,得到RdL中的向量。這個向量是整個圖的最新維度表示。它可以用于圖形分類(例如:這是什么分子?)
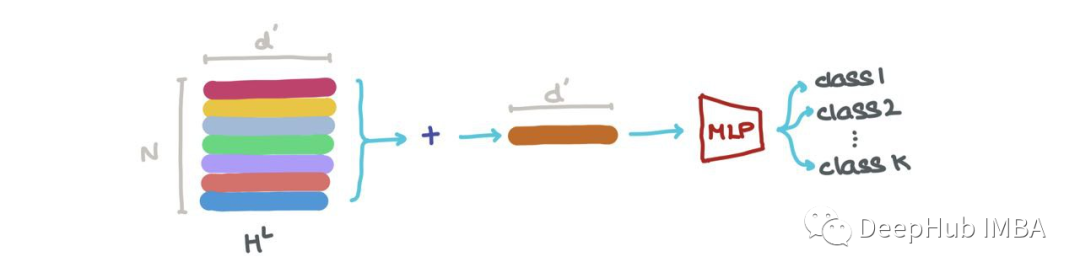
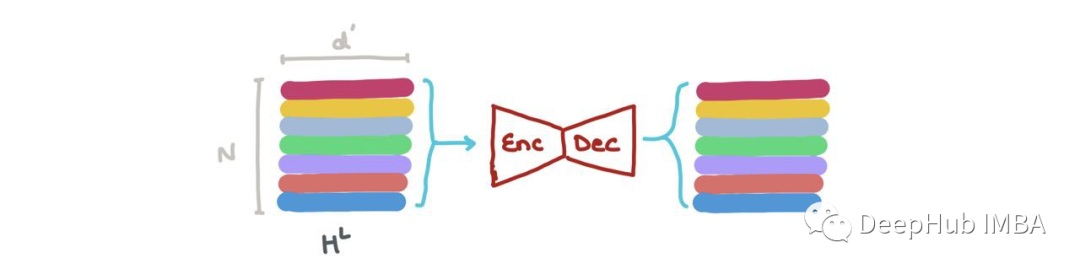
我們可以在HL中連接向量(即?Nk=1hk,其中⊕是向量連接操作),并將其傳遞給一個Graph Autoencoder。當輸入圖有噪聲或損壞,而我們想要重建去噪圖時,就需要這個操作。
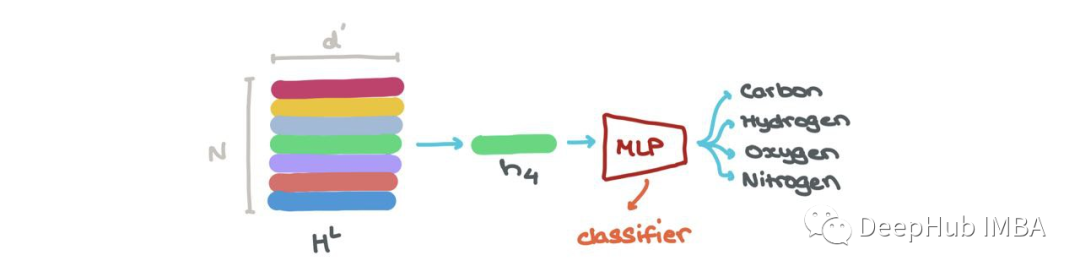
我們可以做節點分類→這個節點屬于什么類?在特定索引hLi (i:1→N)處嵌入的節點可以通過分類器(如MLP)分為K個類(例如:這是碳原子、氫原子還是氧原子?)
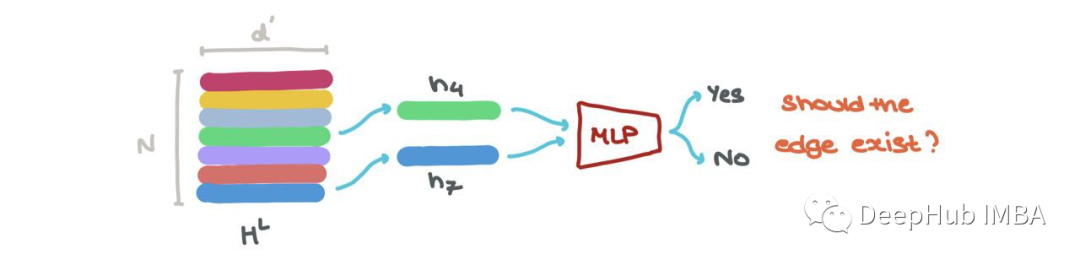
我們還可以進行鏈接預測→某個節點i和j之間是否存在鏈接?hLi和hLj的節點嵌入可以被輸入到另一個基于sigmoid的MLP中,該MLP輸出這些節點之間存在邊的概率。
這些就是GNN在不同的應用中所進行的操作,無論哪種方式,每個h1→N∈HL都可以被堆疊,并被視為一批樣本。我們可以很容易地將其視為批處理。
對于給定的節點i, GNN聚合的第l層具有節點i的l跳鄰域。節點看到它的近鄰,并深入到網絡中,它與鄰居的鄰居交互。
這就是為什么對于非常小、稀疏(很少邊)的圖,大量的GNN層通常會導致性能下降:因為節點嵌入都收斂到一個向量,因為每個節點都看到了許多跳之外的節點。對于小的圖,這是沒有任何作用的。
這也解釋了為什么大多數GNN論文在實驗中經常使用≤4層來防止網絡出現問題。
以節點分類為例訓練GNN
在訓練期間,對節點、邊或整個圖的預測可以使用損失函數(例如:交叉熵)與來自數據集的ground-truth標簽進行比較。也就是說gnn能夠使用反向傳播和梯度下降以端到端方式進行訓練。
訓練和測試數據
與常規ML一樣,圖數據也可以分為訓練和測試。這有兩種方法:
訓練數據和測試數據都在同一個圖中。每個集合中的節點相互連接。只是在訓練期間,測試節點的標簽是隱藏的,而訓練節點的標簽是可見的。但所有節點的特征對于GNN都是可見的。
我們可以對所有節點進行二進制掩碼(如果一個訓練節點i連接到一個測試節點j,只需在鄰接矩陣中設置Aij=0)。
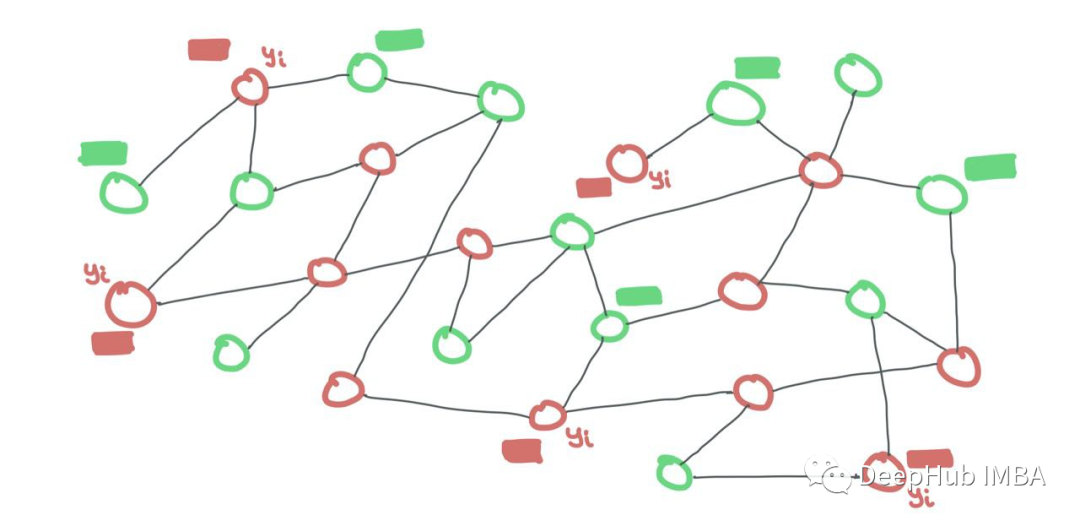
訓練節點和測試節點都是同一個圖的一部分。訓練節點暴露它們的特征和標簽,而測試節點只暴露它們的特征。測試標簽對模型隱藏。二進制掩碼需要告訴GNN什么是訓練節點,什么是測試節點。
2、Inductive
另外一種方法是單獨的訓練圖和測試圖。這類似于常規的ML,其中模型在訓練期間只看到特征和標簽,并且只看到用于測試的特征。訓練和測試在兩個獨立的圖上進行。這些測試圖分布在外,可以檢查訓練期間的泛化質量。
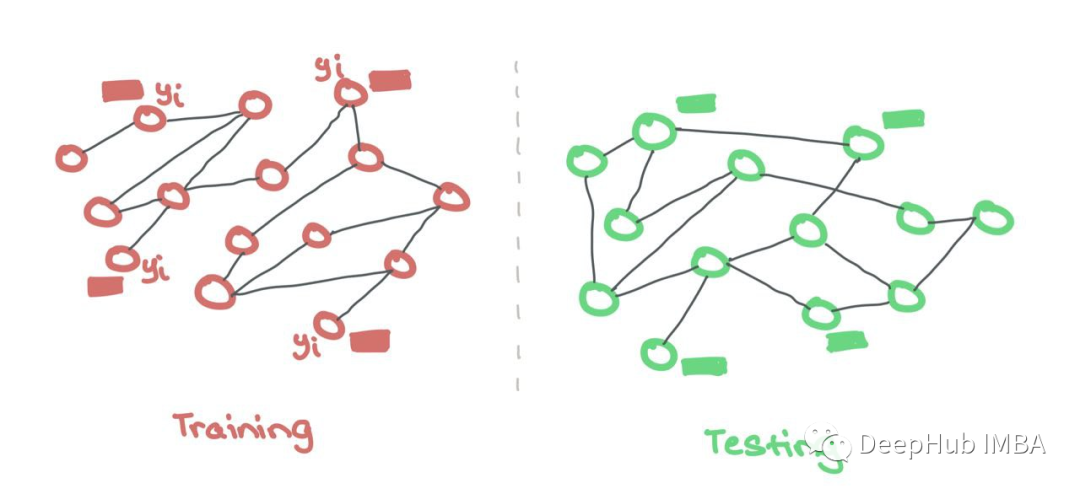
與常規ML一樣,訓練數據和測試數據是分開保存的。GNN只使用來自訓練節點的特征和標簽。這里不需要二進制掩碼來隱藏測試節點,因為它們來自不同的集合。
反向傳播和梯度下降
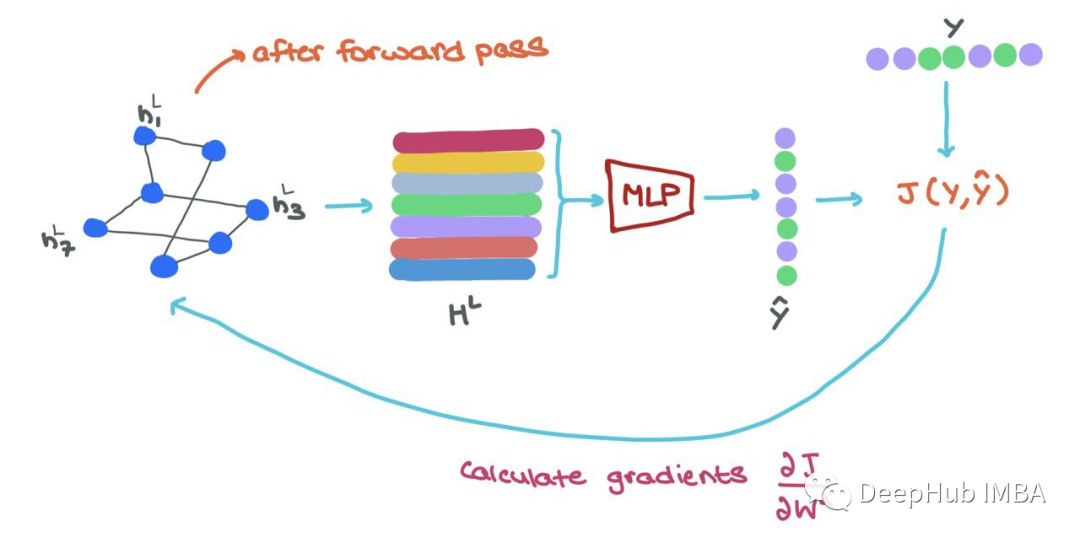
在訓練過程中,一旦我們向前通過GNN,我們就得到了最終的節點表示hLi∈HL, 為了以端到端方式訓練,可以做以下工作:
- 將每個hLi輸入MLP分類器,得到預測^yi
- 使用ground-truth yi和預測yi→J(yi,yi)計算損失
- 使用反向傳播來計算?J/?Wl,其中Wl是來自l層的參數矩陣
- 使用優化器更新GNN中每一層的參數Wl
- (如果需要)還可以微調分類器(MLP)網絡的權重。
-
芯片
+關注
關注
459文章
52145瀏覽量
435938 -
神經網絡
+關注
關注
42文章
4806瀏覽量
102734 -
數學
+關注
關注
0文章
99瀏覽量
19473
發布評論請先 登錄





 詳解圖神經網絡的數學原理2
詳解圖神經網絡的數學原理2
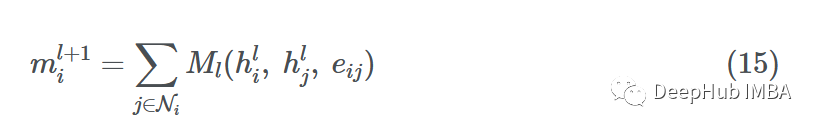










評論