1985年,為了拯救當時出現故障的蘇聯空間站禮炮七號,派出了兩名宇航員進行搶修。在完成任務之后,其中一名宇航員賈尼別科夫打開了從地球帶來的物資。這些物資是用一個翼型螺母鎖緊的,當這個螺母被松開并繼續在空間站漂浮旋轉的時候,賈尼別科夫發現它會周期性地掉轉180度。后來,這個現象被稱為賈尼別科夫效應。
事實上,我們在地球上也能重現該效應。以網球拍為例,我們人為地給它設定三個相互垂直的主軸:一是沿著把柄的主軸,二是垂直于把柄并在網的平面內的主軸,三是垂直于把柄和網的主軸。當我們讓網球拍繞著一或三主軸旋轉并把它拋入空中時,拍子的旋轉是穩定的,它只會繞著初始軸旋轉。當我們讓網球拍繞二主軸旋轉并拋入空中時,它的運動是不穩定的,最后會演變成繞著三個軸旋轉。所以,賈尼別科夫效應又叫作網球拍效應或中間軸效應。
在1991年的時候,一篇公開發表的文章才解釋了這種效應。我也看過一些解釋這種效應的科普文章和視頻,他們要么用純文字進行解釋,要么直接給出歐拉動力學方程的結果進行解釋。今天,我們從推導歐拉動力學方程開始,逐步給出這種效應的解釋。
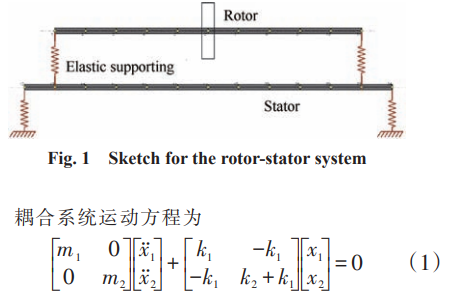
歐拉動力學方程推導
首先,我們要知道力矩和角動量的關系。如果你已經忘了,那么我們可以回想一下力和動量的關系:力等于動量對時間的導數。同樣,力矩等于角動量對時間的導數。
等式的左邊是力矩M,我們可以直接寫出它的分量形式。
等式的右邊是角動量對時間求導,雖然它計算比較復雜,但我們仍然可以寫出分量形式。
接下來這里有一個問題,后三項是基本矢量隨時間的變化,它們取決于我們所取的坐標系。在這里,我們所取的是剛體坐標系。在剛體坐標系下,基本矢量是隨著剛體的旋轉而旋轉,所以基本矢量隨時間的變化就是角速度ω叉乘這個基本矢量。如果還不明白,可以想想高中時是怎么推導圓周運動的加速度。
根據矢量叉乘的法則,最后一項我們可以寫成以下形式。
現在,整個式子變得非常復雜,但是如果我們代入角動量、角速度和轉動慣量的關系,式子就會變得非常簡單。在慣量主軸下,轉動慣量不會隨著旋轉變化,我們有以下關系:
把它代入上面的式子,最終我們會得出這樣的結果:
最后,我們讓每個分量的力矩和每個分量的角動量對時間求導相等,就得到著名的歐拉動力學方程。
網球拍效應解釋
解釋網球拍效應一個很重要的點是理論與現實的差距。理論上,我們可以讓網球拍繞任何一個軸穩定轉動,而繞另外兩個軸轉動的角速度永遠是零。但現實中,我們無法做到這一點,總是會有一些擾動破壞這種理想狀態。現在,我們要研究的是,給了微小擾動之后,這個擾動會不會被放大。
我們假設轉動慣量1>轉動慣量2>轉動慣量3,并且網球拍拋到空中后沒有任何力矩。首先研究繞主軸1旋轉的情況,此時ω1恒定,它對時間的導數也基本為零,而ω2和ω3受到擾動而出現微小的角速度。現在,對歐拉動力學方程的第二個方程求導,并把第三個方程代入其中,我們可以得到:
根據轉動慣量的大小,我們可以知道k<0,是我們很熟悉的波動方程,微小的擾動成正弦變化不會被放大,因此繞主軸1旋轉是穩定的。同樣的道理,我們也可以得出繞主軸3的轉動是穩定的,這里就不再計算。
但是,當繞主軸2旋轉時,同樣的道理我們可以得到:
此時,我們知道k>0,因此擾動會被放大,角速度會增加。也就是說繞主軸2的轉動是不穩定的,一個小擾動就會使網球拍發生翻轉。
審核編輯:郭婷
-
主軸
+關注
關注
0文章
396瀏覽量
4618
原文標題:網球拍效應與歐拉動力學方程
文章出處:【微信號:bdtdsj,微信公眾號:中科院半導體所】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
NVIDIA攜手Ansys和DCAI推進流體動力學量子算法發展
《虛擬世界的力學交響曲:Adams如何重塑工業仿真邊界》
TVolumeX應用:液晶成盒優化
Adams多體動力學仿真解決方案全面解析
輪轂電機驅動電動汽車垂向動力學控制研究綜述
航空發動機整機動力學有限元模型建立方法
【Simcenter STAR-CCM+】通過快速準確的CFD仿真加速空氣動力學創新

使用Phase Lab鎳基動力學數據庫計算多組分合金的成分分布曲線
“本源悟空”超導量子計算機助力大規模流體動力學量子計算

Simcenter STAR-CCM+車輛外部空氣動力學特性——通過快速準確的CFD仿真加速空氣動力學創新

圓滿收官| Aigtek參展第二屆波動力學前沿與應用學術會議載譽歸來!






 網球拍效應與歐拉動力學方程推導
網球拍效應與歐拉動力學方程推導












評論