作者：廖慶陵，竇震海，孫 鍇，朱亞玲

引 言

隨著現(xiàn)代工業(yè)的不斷發(fā)展，電力已經(jīng)深入人們的生產(chǎn)和生活中，負荷預(yù)測則是保證電力系統(tǒng)穩(wěn)定運行的關(guān)鍵技術(shù)。電力負荷數(shù)據(jù)是隨機非平穩(wěn)序列，幾乎不可能達到完全準(zhǔn)確，因此提升預(yù)測精度是學(xué)者們共同追求的目標(biāo)[1?2]。傳統(tǒng)預(yù)測方法在短期預(yù)測上受各種條件影響，在不同地區(qū)、不同情況下表現(xiàn)出來的適應(yīng)性相較于新的智能預(yù)測算法有較大差距。新興的智能預(yù)測算法相對于傳統(tǒng)預(yù)測方法已經(jīng)有了較好的效果，這方面的算法也越來越多，基于極限學(xué)習(xí)機、隨機森林、神經(jīng)網(wǎng)絡(luò)等常見算法的優(yōu)化改良較多。

通常使用其他算法與智能算法相結(jié)合的模式，這種模式能結(jié)合兩種算法的優(yōu)勢，帶來較好的優(yōu)化效果，缺點是可能會導(dǎo)致訓(xùn)練時間變長[6]。文獻[7]采用基于雙種群的粒子群算法（DP?PSO）尋求混合核函數(shù)LS?SV模型的最優(yōu)參數(shù)進行日平均負荷預(yù)測，由于粒子群算法相對容易陷入局部最優(yōu)，得到最佳參數(shù)設(shè)定的成功率得不到保障，從而影響預(yù)測結(jié)果。本文吸取其他算法的先進經(jīng)驗，同時針對粒子群算法的不足，提出一種改進自適應(yīng)粒子群算法優(yōu)化支持向量機模型的負荷預(yù)測。首先選用支持向量機為負荷預(yù)測的工具，支持向量機是在分類與回歸分析中分析數(shù)據(jù)的監(jiān)督式學(xué)習(xí)算法，因為其對于負荷預(yù)測有著很好的效果和實用性，常被應(yīng)用到負荷預(yù)測中。但支持向量機的問題是使用時需要將參數(shù) c和 g 調(diào)到合適的值才能達到最好的預(yù)測分類效果，所以在使用過程中常常會用到各種群體智能算法對支持向量機參數(shù)進行調(diào)優(yōu)。

1 算法原理及改進

1.1 群體算法

大多群體算法都有一個共同的缺點，參數(shù)在程序運行之前就一次性設(shè)置完成，不再變動，使得群體算法在運行前期或后期難以達到最好的優(yōu)化效果。比如粒子群算法中，固定的位置更新公式在運行的后期往往不能達到最優(yōu)的運行效果。針對群體算法位置更新公式的問題，部分改進算法會用到根據(jù)迭代數(shù)進行調(diào)整的位置更新公式，比如帶有慣性因子的粒子群算法，在迭代時對慣性因子進行線性遞減的操作，這樣慣性因子隨著迭代次數(shù)逐漸下降，使得在算法運行的后期粒子群的局部搜索能力得到提高。這種方法的效果要好于固定慣性因子。

但是這種根據(jù)迭代數(shù)線性減少的方式并沒有考慮到每個個體以及種群的實際狀態(tài)，如果前期的搜索并非很有成效，這時貿(mào)然減小粒子群算法中的慣性因子會使得搜索效率降低甚至陷入局部最優(yōu)無法跳出。針對群體算法的參數(shù)調(diào)整或根據(jù)實際運行狀態(tài)動態(tài)調(diào)整的問題，本文提出一種自適應(yīng)動態(tài)因子。將適應(yīng)度函數(shù)算出的適應(yīng)度值作為算法運行狀態(tài)的判斷依據(jù)，根據(jù)每一代種群適應(yīng)度值的變化來動態(tài)調(diào)整參數(shù)，以適應(yīng)各種群體算法的實際運行狀態(tài)。

自適應(yīng)動態(tài)因子更新公式如下：

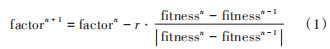
1.2 粒子群算法原理

粒子群算法是一種在生物種群行為特性中得到啟發(fā)的求解優(yōu)化問題的算法。粒子群算法首先初始化一群隨機粒子，然后迭代找到最優(yōu)解，在迭代過程中，粒子通過跟蹤極值加上更新公式來更新位置。算法流程如下：

1）初始化：首先設(shè)置最大迭代次數(shù)、目標(biāo)函數(shù)的自變量個數(shù)、粒子的最大速度，在速度區(qū)間和搜索空間上隨機初始化速度和位置，設(shè)置粒子群規(guī)模，每個粒子隨機初始化。

2）根據(jù)適應(yīng)度函數(shù)計算每個粒子的適應(yīng)度，得到個體極值與全局最優(yōu)解。3）通過式（2）、式（3）更新速度和位置。

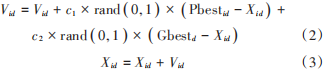
式中：Vid 是粒子 i 在第 d 維度的速度；c1 和 c2 為加速常數(shù)；rand ( 0, 1 ) 是值為大于 0 且小于 1 的隨機數(shù)；Pbestid是粒子 i在第 d維度的最好位置；Gbestd是全部粒子在第d維度的最好位置。

4）達到設(shè)定的迭代次數(shù)。

和其他群體智能算法一樣，粒子群算法在優(yōu)化過程中，種群的多樣性和算法的收斂速度之間始終存在著矛盾。對標(biāo)準(zhǔn)粒子群算法的改進，無論是參數(shù)的選取或是其他技術(shù)與粒子群的融合，其目的都是希望在加強算法局部搜索能力的同時保持種群的多樣性，防止算法在快速收斂的同時不容易出現(xiàn)早熟。

1.3 粒子群算法的改進

1.3.1 混沌初始化

種群初始化對于粒子群算法的求解精度和收斂速度有著較大的影響。粒子群算法的第一步初始化：傳統(tǒng)粒子群算法一般采用隨機初始化來確定初始種群的位置分布，由計算機生成隨機數(shù)，再根據(jù)式（4）隨機生成各個粒子的初始位置。通常這種隨機初始化能生成每次不一樣的初始種群，使用起來比較方便。但也存在弊端，就是初始粒子在解空間的分布并不均勻，常常遇到局部區(qū)域的粒子過于密集，同時一部分區(qū)域的初始粒子卻過于稀疏。這樣的情況對優(yōu)化算法的前期收斂是非常不利的，對于容易陷入局部最優(yōu)的群體優(yōu)化算法，可能導(dǎo)致收斂速度下降甚至無法收斂的情況發(fā)生。

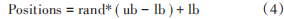
式中：Positions 代表生成的粒子位置；rand 代表生成的隨機數(shù)，取值范圍為[0，1]；ub，lb 分別為解空間的上下界。

而混沌初始化則可以有效地避免這些問題。混沌初始化具有隨機性、遍歷性和規(guī)律性的特點，是在一定范圍內(nèi)按照自身規(guī)律不重復(fù)地遍歷搜索空間，這樣生成的初始種群在求解精度和收斂速度方面有著明顯改進。本文中的混沌初始化選用 TentMap 混沌模型，其公式如下：

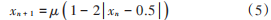
式中：μ ∈ ( 0, 4 ]，為混沌模型的映射參數(shù)，本文中 μ 的取值為 1，使混沌系統(tǒng)處于完全混沌狀態(tài)；xn是由混沌系統(tǒng)生成的混沌數(shù)字；x0為初始值，本文中取值為 0.588。

1.3.2 動態(tài)自適應(yīng)慣性因子

原始的粒子群算法中是不含有慣性因子的，但是使用效果不夠好，所以在使用過程中，普遍使用的是帶有慣性因子的粒子群算法。比較常見的慣性因子有：常數(shù)慣性因子、線性下降慣性因子和模糊慣性因子。算法在搜索最優(yōu)點時，全局搜索能力與局部搜索能力不能顧此失彼。慣性因子 ω 就能在一定程度上起到平衡的作用，增大 ω 可以加強全局探測能力，而減小 ω 則能加強局部搜索能力。帶有慣性權(quán)重的粒子速度更新公式為：

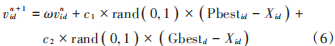
式中 ω是慣性因子，為一個非負數(shù)。常數(shù)慣性因子粒子群算法相較于原始粒子群算法在使用效果上有較大優(yōu)勢，能調(diào)節(jié)粒子群的全局搜索能力或者局部搜索能力，但是常數(shù)慣性因子并不能同時兼顧，于是又有學(xué)者提出一種隨著迭代次數(shù)的增加線性降低慣性因子的方法。線性下降慣性因子的計算公式如下：

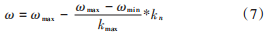
式中：ωmax 和 ωmin 分別是慣性因子的最大和最小值；kn 為當(dāng)前迭代數(shù)；kmax是最大迭代數(shù)。

線性下降慣性因子的粒子群算法在開始時慣性較大，適合大面積的搜索，能快速找到最優(yōu)解的大致位置，之后隨著 ω 逐漸減小，粒子慣性減弱，加強局部搜索能力，能更精確地搜尋最優(yōu)解。這種方法相較于常數(shù)慣性因子粒子群算法有較大的提升，但是因為不管是否適應(yīng)度變得更好，慣性因子都會以同樣的速度下降，所以線性下降慣性因子粒子群算法有時也會出現(xiàn)尋優(yōu)效果差的問題。本文吸取前人改進算法的優(yōu)點，提出一種動態(tài)自適應(yīng)慣性因子。每次迭代更新所有粒子的位置后計算所有粒子的適應(yīng)度，如果種群適應(yīng)度比上一代種群適應(yīng)度更好，那么調(diào)小慣性因子 ω，粒子群的局部搜索能力就會得到提高。相反，如果種群適應(yīng)度降低，就調(diào)大慣性因子 ω，粒子群的局部搜索能力就會得到減弱，全局搜索性能得到提升。動態(tài)自適應(yīng) ω的計算公式如下：

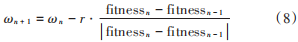
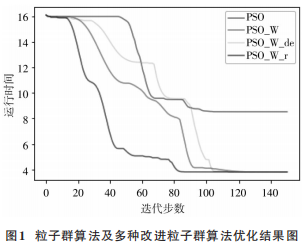
式中：fitnessn為周期n時的最優(yōu)適應(yīng)度值；ωn為周期n時ω的 值 ，ω的取值范圍是 [0.4,0.9],初始值設(shè)置為0.75；r為增益倍數(shù)，取值范圍是[0.02,0.05]。用經(jīng)典粒子群優(yōu)化（PSO）算法、慣性粒子群優(yōu)化（PSO_W）算 法、線性下降慣性因子粒子群優(yōu)化（PSO_W_de）算法和自適應(yīng)動態(tài)粒子群優(yōu)化（PSO_W_r）算法對函數(shù)進行尋優(yōu)，運行結(jié)果如圖 1 所示。可以從圖中看出，通過自適應(yīng)慣性因子改進的粒子群算法在效率上遠遠高于其他幾種粒子群算法。

1.3.3 差分變異算子

粒子群優(yōu)化算法雖然有運行速度快的優(yōu)點，但是不可避免地容易陷入局部最優(yōu)。本文將差分算法中的差分變異算子引入粒子群算法中：在每次迭代完成之后，選取適應(yīng)度最差的30%~50% 的粒子進行變異操作。這樣可以在加快尋優(yōu)速度的同時，防止算法陷入早熟。變異公式如下：

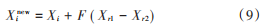
式中：Xi 為變異前的粒子 i；Xinew 為變異后的粒子 i；F 為縮放比例因子，通常取值為 0.5。

2 自適應(yīng)粒子群算法優(yōu)化支持向量機模型

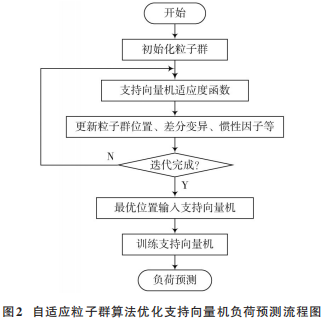
支持向量機中有兩個重要參數(shù)c和g。其中：c 是懲罰系數(shù)，是對誤差的寬容度，c越高越容易過擬合，c過小則容易欠擬合；g 是 RBF 內(nèi)核中的一個參數(shù)，g 值越大，支持向量越少，g 值越小，支持向量越多。支持向量的個數(shù)影響訓(xùn)練與預(yù)測的速度。因此在支持向量機的使用中，參數(shù)的優(yōu)化會帶來更好的效果。本文選擇粒子群優(yōu)化算法以及自適應(yīng)粒子群優(yōu)化算法對支持向量機的參數(shù) c 和 g 進行調(diào)優(yōu)，使得負荷預(yù)測模型能有更好的預(yù)測效果。用自適應(yīng)粒子群算法優(yōu)化支持向量機參數(shù)進行負荷預(yù)測的具體實現(xiàn)步驟如下：

1）混沌初始化粒子群的初始位置，每個位置的坐標(biāo)值代表支持向量機參數(shù)c和 g。

2）計算出每個粒子對應(yīng)的適應(yīng)度，適應(yīng)度函數(shù)選用支持向量機模型里的適應(yīng)度函數(shù)。

3）再根據(jù)自適應(yīng)粒子群算法的位置更新公式進行移動，同時根據(jù)適應(yīng)度值的變化，動態(tài)調(diào)整慣性因子 ω。

4）將適應(yīng)度較差的一部分粒子進行差分變異。并且重新回到步驟 2），直到達到迭代次數(shù)。

5）將適應(yīng)度最好的粒子的位置參數(shù)取出，作為支持向量機的參數(shù)c和g。

6）用訓(xùn)練數(shù)據(jù)對當(dāng)前支持向量機進行訓(xùn)練。

7）用訓(xùn)練好的支持向量機模型進行負荷預(yù)測，輸出結(jié)果。

自適應(yīng)粒子群算法優(yōu)化支持向量機模型簡要流程圖如圖2所示。

本文用粒子群算法優(yōu)化的支持向量機和改進的自適應(yīng)粒子群算法優(yōu)化的支持向量機進行負荷預(yù)測，并將結(jié)果進行對比分析。兩種算法都采用相同的數(shù)據(jù)、相同的輸入輸出量。本文采用美國某地區(qū)2019年8—9月的歷史負荷值作為實驗數(shù)據(jù)，共 1 464 個每小時一次的負荷數(shù)據(jù)，輸出量為一天中每個小時的負荷預(yù)測值，輸入量為預(yù)測點當(dāng)天前一個和前兩個小時的負荷值，前一天同一小時、前一小時、后一小時負荷值，前一周同一小時、前一小時、后一小時負荷數(shù)據(jù)。對輸入數(shù)據(jù)需要進行歸一化預(yù)處理，以提高算法運行效率以及預(yù)測精度。預(yù)處理方法是用線性轉(zhuǎn)化的方式將數(shù)據(jù)成比例地轉(zhuǎn)化到[0，1]區(qū)間內(nèi)。這樣將數(shù)據(jù)限定在一個較小范圍，預(yù)處理公式如下：

式中：x 是原始數(shù)據(jù)；x′是處理后的數(shù)據(jù)；xmax 和 xmin 分別為輸入樣本集的最大值和最小值。粒子群算法種群規(guī)模取 40，增益倍數(shù) r 取 10，迭代次數(shù) Kmax 取 100。預(yù)測結(jié)果如圖 3所示。

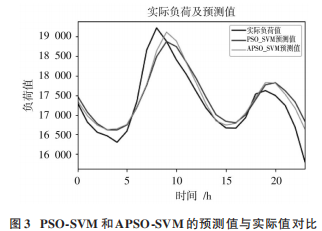
根據(jù)實例數(shù)據(jù)，利用式（11）分析可以得出：在迭代次數(shù)為 100 次的情況下，改進自適應(yīng)粒子群算法優(yōu)化的支持向量機預(yù)測值的 MAPE 值為 1.569%；原始粒子群算法在同樣迭代次數(shù)的情況下誤差相對較大，MAPE 值為 2.248%。

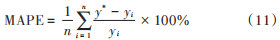
式中：y ?為預(yù)測值；yi為實際值；n為樣本量。

3 結(jié) 語

傳統(tǒng)的粒子群優(yōu)化算法的慣性因子為固定值，導(dǎo)致前期或后期效率較低。自適應(yīng)慣性因子使得粒子群的慣性因子在算法運行過程中根據(jù)適應(yīng)度自動調(diào)整，以達到提升搜索效率的目的，同時針對粒子群算法容易陷入局部最優(yōu)的問題提出加入差分變異算法，對適應(yīng)度差的粒子進行差分變異，并用改進后的自適應(yīng)粒子群算法優(yōu)化支持向量機參數(shù) c 和 g，得到一種自適應(yīng)粒子群算法優(yōu)化的支持向量機模型，使得支持向量機與粒子群優(yōu)化算法能很好地配合進行負荷預(yù)測。自適應(yīng)粒子群算法可以使得這個優(yōu)化過程相對于原始粒子群算法更加高效，這主要得益于改進的自適應(yīng)慣性因子相較于傳統(tǒng)的固定慣性因子，同時增強了前期的全局搜索能力和后期局部搜索能力，從而更快速尋找到更優(yōu)的支持向量機參數(shù)。根據(jù)實際數(shù)據(jù)進行實驗，對比本文提出的模型與未經(jīng)優(yōu)化的模型，發(fā)現(xiàn)預(yù)測精度有明顯提升。

盡管如此，本文方法仍有改進空間。以后的工作可以從以下兩方面著手：需對粒子群算法的智能搜索策略、慣性因子、學(xué)習(xí)因子和其他重要參數(shù)的取值進行更加深入的分析，繼續(xù)挖掘粒子群算法的尋優(yōu)潛力；將APSO?SVM 算法運用于更多的領(lǐng)域，提升改進算法的應(yīng)用范圍，使其具有更好的推廣價值。

審核編輯：郭婷