挺久沒寫動態(tài)規(guī)劃相關(guān)的題目了,本文我?guī)Т蠹覐?fù)習(xí)一下動態(tài)規(guī)劃相關(guān)問題的一系列解題套路,然后著重討論一下動態(tài)規(guī)劃窮舉時不同視角的問題。
動態(tài)規(guī)劃解題組合拳
首先,前文我的刷題心得講了,我們刷的算法問題的本質(zhì)是「窮舉」,動態(tài)規(guī)劃問題也不例外,你必須想辦法窮舉所有可能的解,然后從中篩選出符合題目要求的解。
另外,動態(tài)規(guī)劃問題窮舉的過程中會出現(xiàn)重疊子問題導(dǎo)致的冗余計算,所以前文動態(tài)規(guī)劃核心套路框架中告訴你如何一步一步把暴力窮舉解法優(yōu)化成效率更高的動態(tài)規(guī)劃解法。
然而,想要寫出暴力解需要依據(jù)狀態(tài)轉(zhuǎn)移方程,狀態(tài)轉(zhuǎn)移方程是動態(tài)規(guī)劃的解題核心,可不是那么容易想出來的。不過,前文動態(tài)規(guī)劃設(shè)計:數(shù)學(xué)歸納法告訴你,思考狀態(tài)轉(zhuǎn)移方程的一個基本方法是數(shù)學(xué)歸納法,即明確dp函數(shù)或數(shù)組的定義,然后使用這個定義,從已知的「狀態(tài)」中推導(dǎo)出未知的「狀態(tài)」。
還沒完,比如高樓扔雞蛋問題中對dp函數(shù)/數(shù)組的定義不見得是唯一的,不同的定義會導(dǎo)致狀態(tài)轉(zhuǎn)移方程發(fā)生變化,解題效率也有高低之分,所以我們應(yīng)該給dp函數(shù)盡可能想出更合適的定義來解題。
接下來就是本文要著重探討的問題了:就算dp函數(shù)/數(shù)組的定義相同,如果你使用不同的「視角」進行窮舉,效率也不見得是相同的。
關(guān)于窮舉「視角」的問題,前文回溯算法窮舉視角:子集劃分問題講了回溯算法中不同的窮舉視角導(dǎo)致的不同解法,其實這種視角的切換在動態(tài)規(guī)劃類型問題中依然存在。前文對排列的舉例非常有助于你理解窮舉視角的問題,這里再簡單提一下。
排列問題的兩種視角
我們先回顧一下以前學(xué)過的排列組合知識:
1、P(n, k)(也有很多書寫成A(n, k))表示從n個不同元素中拿出k個元素的排列(Permutation/Arrangement);C(n, k)表示從n個不同元素中拿出k個元素的組合(Combination)總數(shù)。
2、「排列」和「組合」的主要區(qū)別在于是否考慮順序的差異。
3、排列和組合總數(shù)的計算公式如下:
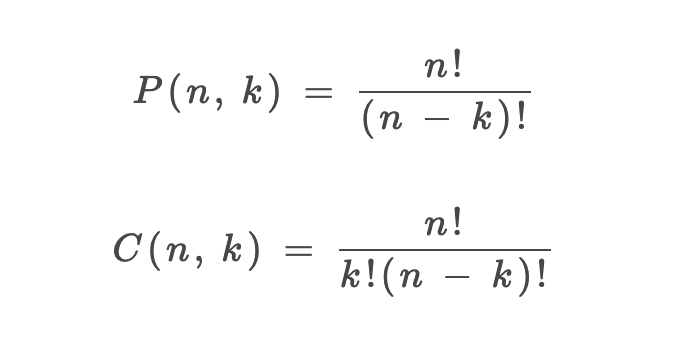
好,現(xiàn)在我問一個問題,這個排列公式P(n, k)是如何推導(dǎo)出來的?為了搞清楚這個問題,我需要講一點組合數(shù)學(xué)的知識。
排列組合問題的各種變體都可以抽象成「球盒模型」,P(n, k)就可以抽象成下面這個場景:

即,將n個標(biāo)記了不同序號的球(標(biāo)號為了體現(xiàn)順序的差異),放入k個標(biāo)記了不同序號的盒子中(其中n >= k,每個盒子最終都裝有恰好一個球),共有P(n, k)種不同的方法。
現(xiàn)在你來,往盒子里放球,你怎么放?其實有兩種視角。
首先,你可以站在盒子的視角,每個盒子必然要選擇一個球。
這樣,第一個盒子可以選擇n個球中的任意一個,然后你需要讓剩下k - 1個盒子在n - 1個球中選擇:
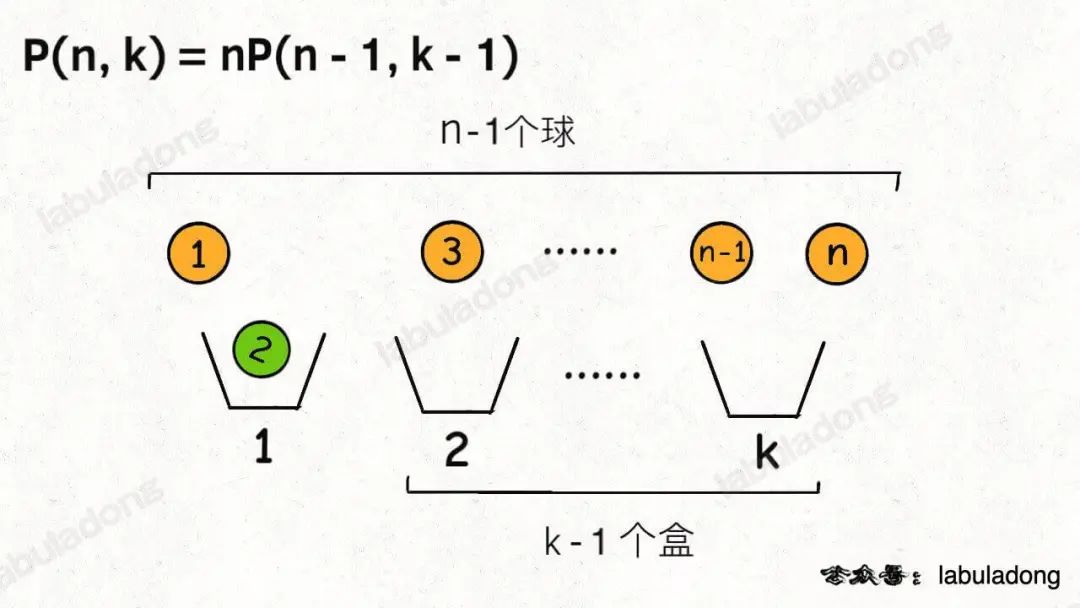
另外,你也可以站在球的視角,因為并不是每個球都會被裝進盒子,所以球的視角分兩種情況:
1、第一個球可以不裝進任何一個盒子,這樣的話你就需要將剩下n - 1個球放入k個盒子。
2、第一個球可以裝進k個盒子中的任意一個,這樣的話你就需要將剩下n - 1個球放入k - 1個盒子。
結(jié)合上述兩種情況,可以得到:
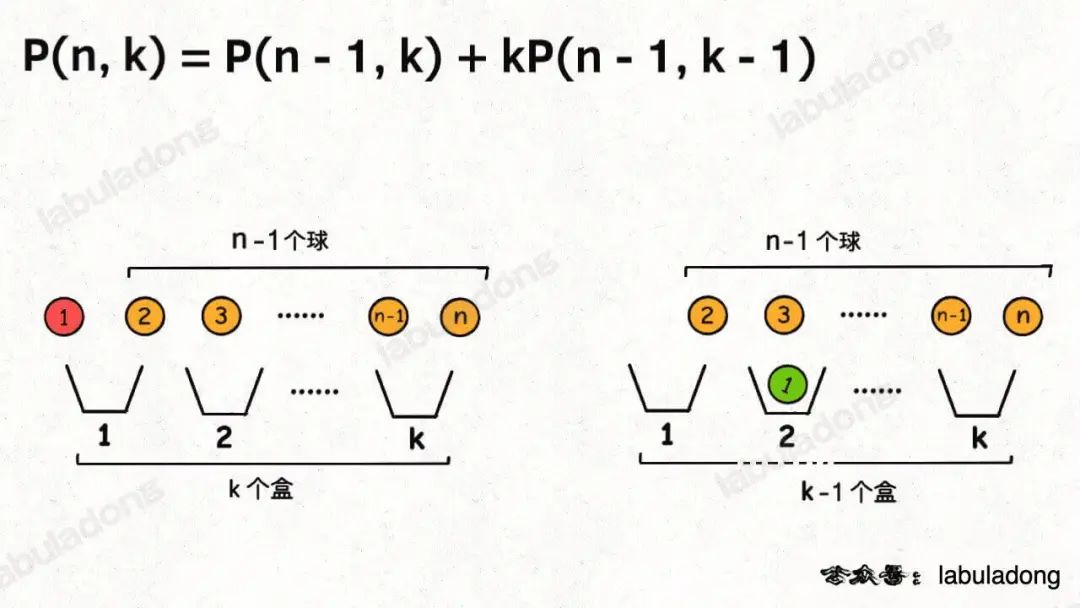
你看,兩種視角得到兩個不同的遞歸式,但這兩個遞歸式解開的結(jié)果都是我們熟知的階乘形式:
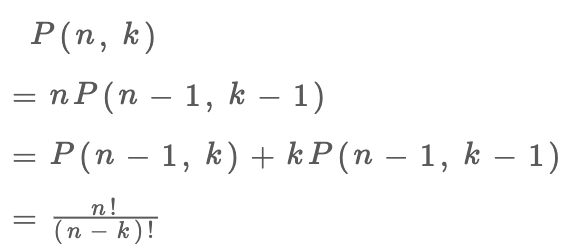
至于如何解遞歸式,涉及數(shù)學(xué)的內(nèi)容比較多,這里就不做深入探討了,有興趣的讀者可以自行學(xué)習(xí)組合數(shù)學(xué)相關(guān)知識。
當(dāng)然,以上只是純數(shù)學(xué)的推導(dǎo),P(n, k)的計算結(jié)果也僅僅是一個數(shù)字,所以以上兩種窮舉視角從數(shù)學(xué)上講沒什么差異。但從編程的角度來看,如果讓你計算出來所有排列結(jié)果,那么兩種窮舉思路的代碼實現(xiàn)可能會產(chǎn)生性能上的差異,因為有的窮舉思路難免會使用額外的 for 循環(huán)拖慢效率,這也是前文回溯算法窮舉視角:子集劃分問題主要探討的。
本文不講回溯算法和排列組合,不過請你記住這個例子,待會會把這種窮舉視角的差異運用到動態(tài)規(guī)劃題目當(dāng)中。
例題分析
看一下力扣第 115 題「不同的子序列」:給你輸入一個字符串s和一個字符串t,請你計算在s的子序列中t出現(xiàn)的次數(shù)。比如題目給的例子,輸入s = "babgbag", t = "bag",算法返回 5:

函數(shù)簽名如下:
intnumDistinct(Strings,Stringt);
你要數(shù)一數(shù)s的子序列中有多少個t,說白了就是窮舉嘛,那么首先想到的就是能不能把原問題分解成規(guī)模更小的子問題,然后通過子問題的答案推導(dǎo)出原問題的答案。
首先,我們可以這樣定義一個dp函數(shù):
//定義:s[i..]的子序列中 t[j..]出現(xiàn)的次數(shù)為 dp(s, i, t, j)
intdp(Strings,inti,Stringt,intj)
這道題對dp函數(shù)的定義很簡單直接,題目讓你求出現(xiàn)次數(shù),那你就定義函數(shù)返回值為出現(xiàn)次數(shù)就可以。
有了這個dp函數(shù),題目想要的結(jié)果是dp(s, 0, t, 0),base case 也很容易寫出來,解法框架如下:
intnumDistinct(Strings,Stringt){
returndp(s,0,t,0);
}
//定義:s[i..]的子序列中 t[j..]出現(xiàn)的次數(shù)為 dp(s, i, t, j)
intdp(Strings,inti,Stringt,intj){
//basecase1
if(j==t.length()){
//t已經(jīng)全部匹配完成
return1;
}
//basecase2
if(s.length()-i// s[i..]比 t[j..]還短,必然沒有匹配的子序列
return0;
}
//...
}
好,接下來開始思考如何利用這個dp函數(shù)將大問題分解成小問題,即如何寫出狀態(tài)轉(zhuǎn)移方程進行窮舉。
回顧一下之前講的排列組合的「球盒模型」,這里是不是很類似?t中的若干字符就好像若干盒子,s中的若干字符就好像若干小球,你需要做的就是給所有盒子都裝一個小球。
所以這里就有兩種窮舉思路了,分別是站在t的視角(盒子選擇小球)和站在s的視角(小球選擇盒子)。
視角一,站在t的角度進行窮舉:
我們的原問題是求s[0..]的所有子序列中t[0..]出現(xiàn)的次數(shù),那么可以先看t[0]在s中的什么位置,假設(shè)s[2], s[6]是字符t[0],那么原問題轉(zhuǎn)化成了在s[2..]和s[6..]的所有子序列中計算t[1..]出現(xiàn)的次數(shù)。
寫成比較偏數(shù)學(xué)的形式就是狀態(tài)轉(zhuǎn)移方程:
--定義:s[i..]的子序列中 t[j..]出現(xiàn)的次數(shù)為 dp(s, i, t, j)
dp(s,i,t,j)=SUM(dp(s,k+1,t,j+1)wherek>=iands[k]==t[j])
翻譯成代碼大致就是這個思路:
//定義:s[i..]的子序列中 t[j..]出現(xiàn)的次數(shù)為 dp(s, i, t, j)
intdp(Strings,inti,Stringt,intj){
intres=0;
//在s[i..]中尋找k,使得s[k]==t[j]
for(intk=i;kif(s.charAt(k)==t.charAt(j)){
//累加結(jié)果
res+=dp(s,k+1,t,j+1);
}
}
returnres;
}
這個思路應(yīng)該不難理解吧,當(dāng)然還可以加上備忘錄消除重疊子問題,最終解法如下:
//備忘錄
int[][]memo;
intnumDistinct(Strings,Stringt){
//初始化備忘錄為特殊值-1
memo=newint[s.length()][t.length()];
for(int[]row:memo){
Arrays.fill(row,-1);
}
returndp(s,0,t,0);
}
//定義:s[i..]的子序列中 t[j..]出現(xiàn)的次數(shù)為 dp(s, i, t, j)
intdp(Strings,inti,Stringt,intj){
//basecase1
if(j==t.length()){
return1;
}
//basecase2
if(s.length()-ireturn0;
}
//查備忘錄防止冗余計算
if(memo[i][j]!=-1){
returnmemo[i][j];
}
intres=0;
//執(zhí)行狀態(tài)轉(zhuǎn)移方程
//在s[i..]中尋找k,使得s[k]==t[j]
for(intk=i;kif(s.charAt(k)==t.charAt(j)){
//累加結(jié)果
res+=dp(s,k+1,t,j+1);
}
}
//存入備忘錄
memo[i][j]=res;
returnres;
}
這道題就解決了,不過效率不算很高,我們可以粗略估算一下這個算法的時間復(fù)雜度上界,其中M, N分別代表s, t的長度,算法的「狀態(tài)」就是dp函數(shù)參數(shù)i, j的組合:
帶備忘錄的動態(tài)規(guī)劃算法的時間復(fù)雜度
=子問題的個數(shù)x函數(shù)本身的時間復(fù)雜度
=「狀態(tài)」的個數(shù)x函數(shù)本身的時間復(fù)雜度
=O(MN)*O(M)
=O(N*M^2)
當(dāng)然,因為 for 循環(huán)的復(fù)雜度不總是 O(M) 且子問題個數(shù)肯定小于 O(MN),所以這是復(fù)雜度的粗略上界。不過根據(jù)前文算法時空復(fù)雜度使用指南的描述,這個上界還是說明這個算法的復(fù)雜度有些偏高。主要高在哪里呢?對「狀態(tài)」的窮舉已經(jīng)有了memo備忘錄的優(yōu)化,所以 O(MN) 的復(fù)雜度是必不可少的,關(guān)鍵問題出在dp函數(shù)中的 for 循環(huán)。
是否可以優(yōu)化掉dp函數(shù)中的 for 循環(huán)呢?可以的,這就需要另一種窮舉視角來解決這個問題。
視角二,站在s的角度進行窮舉:
我們的原問題是計算s[0..]的所有子序列中t[0..]出現(xiàn)的次數(shù),可以先看看s[0]是否能匹配t[0],如果不匹配,那沒得說,原問題就可以轉(zhuǎn)化為計算s[1..]的所有子序列中t[0..]出現(xiàn)的次數(shù);
但如果s[0]可以匹配t[0],那么又有兩種情況,這兩種情況是累加的關(guān)系:
1、讓s[0]匹配t[0],那么原問題轉(zhuǎn)化為在s[1..]的所有子序列中計算t[1..]出現(xiàn)的次數(shù)。
2、不讓s[0]匹配t[0],那么原問題轉(zhuǎn)化為在s[1..]的所有子序列中計算t[0..]出現(xiàn)的次數(shù)。
為啥明明s[0]可以匹配t[0],還不讓它倆匹配呢?主要是為了給s[0]之后的元素匹配的機會,比如s = "aab", t = "ab",就有兩種匹配方式:a_b和_ab。
把以上思路寫成狀態(tài)轉(zhuǎn)移方程:
//定義:s[i..]的子序列中 t[j..]出現(xiàn)的次數(shù)為 dp(s, i, t, j)
intdp(Strings,inti,Stringt,intj){
if(s[i]==t[j]){
//匹配,兩種情況,累加關(guān)系
returndp(s,i+1,t,j+1)+dp(s,i+1,t,j);
}else{
//不匹配,在s[i+1..]的子序列中計算t[j..]的出現(xiàn)次數(shù)
returndp(s,i+1,t,j);
}
}
依照這個思路,再加個備忘錄消除重疊子問題,可以寫出如下解法:
int[][]memo;
intnumDistinct(Strings,Stringt){
//初始化備忘錄為特殊值-1
memo=newint[s.length()][t.length()];
for(int[]row:memo){
Arrays.fill(row,-1);
}
returndp(s,0,t,0);
}
//定義:s[i..]的子序列中 t[j..]出現(xiàn)的次數(shù)為 dp(s, i, t, j)
intdp(Strings,inti,Stringt,intj){
//basecase1
if(j==t.length()){
return1;
}
//basecase2
if(s.length()-ireturn0;
}
//查備忘錄防止冗余計算
if(memo[i][j]!=-1){
returnmemo[i][j];
}
intres=0;
//執(zhí)行狀態(tài)轉(zhuǎn)移方程
if(s.charAt(i)==t.charAt(j)){
//匹配,兩種情況,累加關(guān)系
res+=dp(s,i+1,t,j+1)+dp(s,i+1,t,j);
}else{
//不匹配,在s[i+1..]的子序列中計算t[j..]的出現(xiàn)次數(shù)
res+=dp(s,i+1,t,j);
}
//結(jié)果存入備忘錄
memo[i][j]=res;
returnres;
}
這個解法中dp函數(shù)遞歸的次數(shù),即狀態(tài)i, j的不同組合的個數(shù)為 O(MN),而dp函數(shù)本身沒有 for 循環(huán),即時間復(fù)雜度為 O(1),所以算法總的時間復(fù)雜度就是 O(MN),比剛才的解法要好一些,你提交這個解法代碼,耗時明顯比剛才的解法少一些。
至此,這道題就分析完了。我們分別站在t的視角和s的視角運用dp函數(shù)的定義進行窮舉,得出兩種完全不同但都是正確的狀態(tài)轉(zhuǎn)移邏輯,不過兩種邏輯在代碼實現(xiàn)上有效率的差異。
那么不妨進一步思考一下,什么樣的動態(tài)規(guī)劃題目可能產(chǎn)生「窮舉視角」上的差異?換句話說,什么樣的動態(tài)規(guī)劃問題能夠抽象成經(jīng)典的「球盒模型」呢?
--- EOF ---
審核編輯 :李倩
-
函數(shù)
+關(guān)注
關(guān)注
3文章
4380瀏覽量
64845 -
數(shù)組
+關(guān)注
關(guān)注
1文章
420瀏覽量
26539
原文標(biāo)題:論動態(tài)規(guī)劃窮舉的兩種視角
文章出處:【微信號:TheAlgorithm,微信公眾號:算法與數(shù)據(jù)結(jié)構(gòu)】歡迎添加關(guān)注!文章轉(zhuǎn)載請注明出處。
發(fā)布評論請先 登錄
貼片晶振中兩種常見封裝介紹
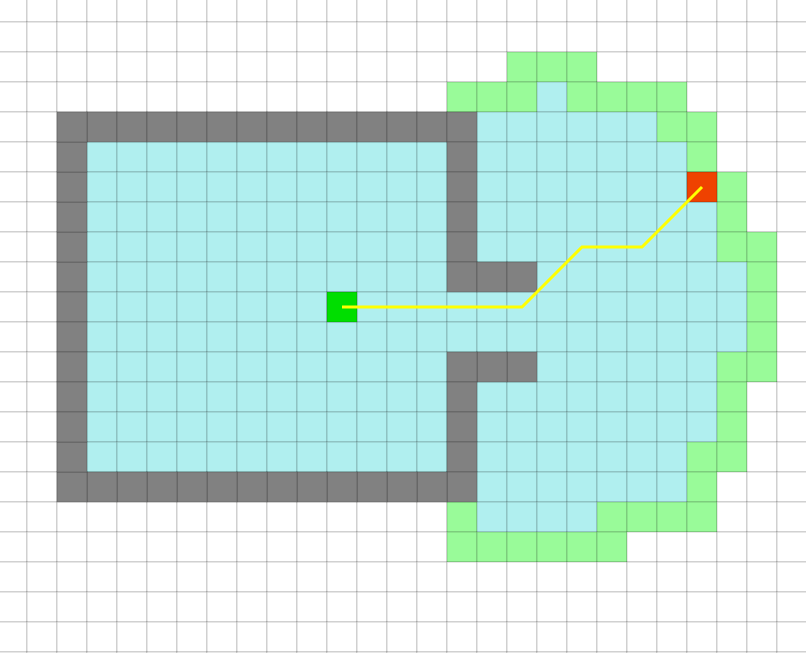
AGV小車中的動態(tài)路徑規(guī)劃算法揭秘
詳解ADC電路的靜態(tài)仿真和動態(tài)仿真

AMC1204有兩種封裝,SOIC-8和SOIC-16,功能一樣嗎?為什么要推出兩種封裝?
ADS1292R有 \"1 ch ECG + 1 ch呼吸偵測\" 或 \"2 ch ECG\" 兩種模式,是否可以在產(chǎn)品上實現(xiàn)自行切換兩種使用模式?
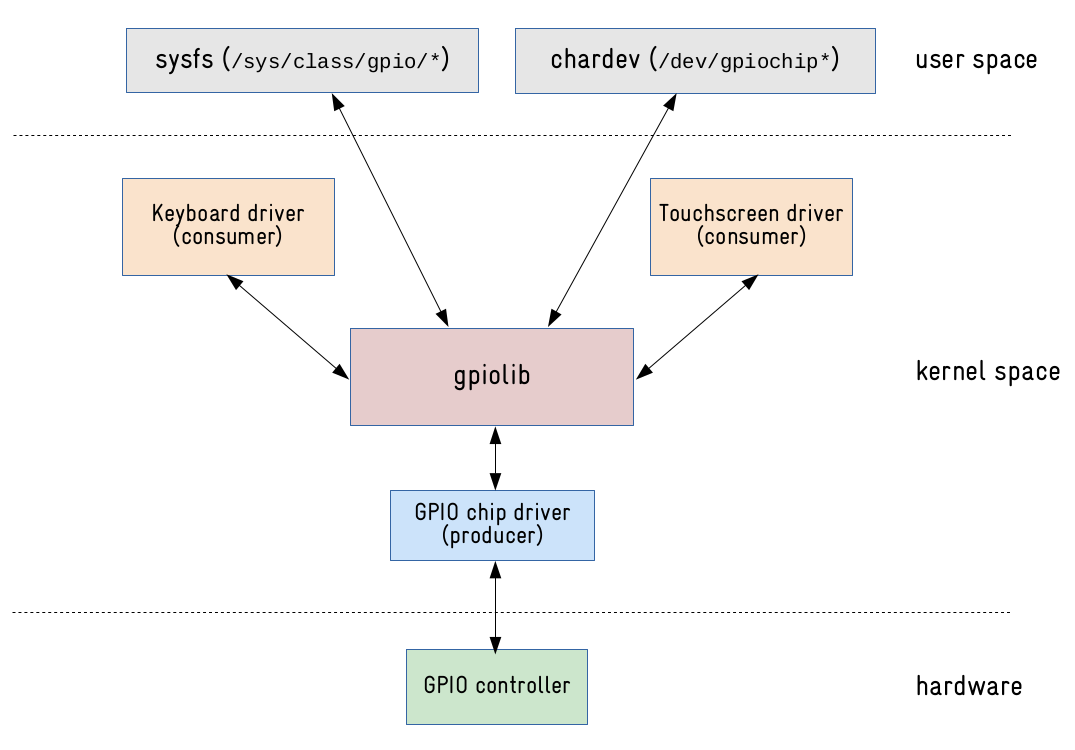
Linux應(yīng)用層控制外設(shè)的兩種不同的方式
比較分析兩種不同的可提高柵極驅(qū)動電流的方法






 論動態(tài)規(guī)劃窮舉的兩種視角
論動態(tài)規(guī)劃窮舉的兩種視角











評論