昨天第二篇文章寫的有點匆忙了，有一些地方配圖配錯了，這里做個更正。

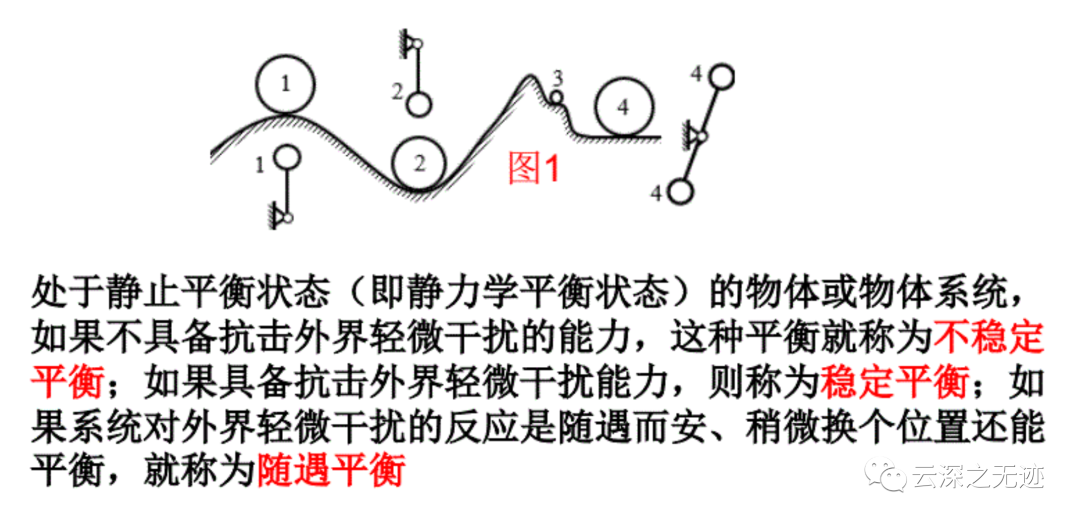
關(guān)于靜力學(xué)平衡，就回憶一下這個圖就好

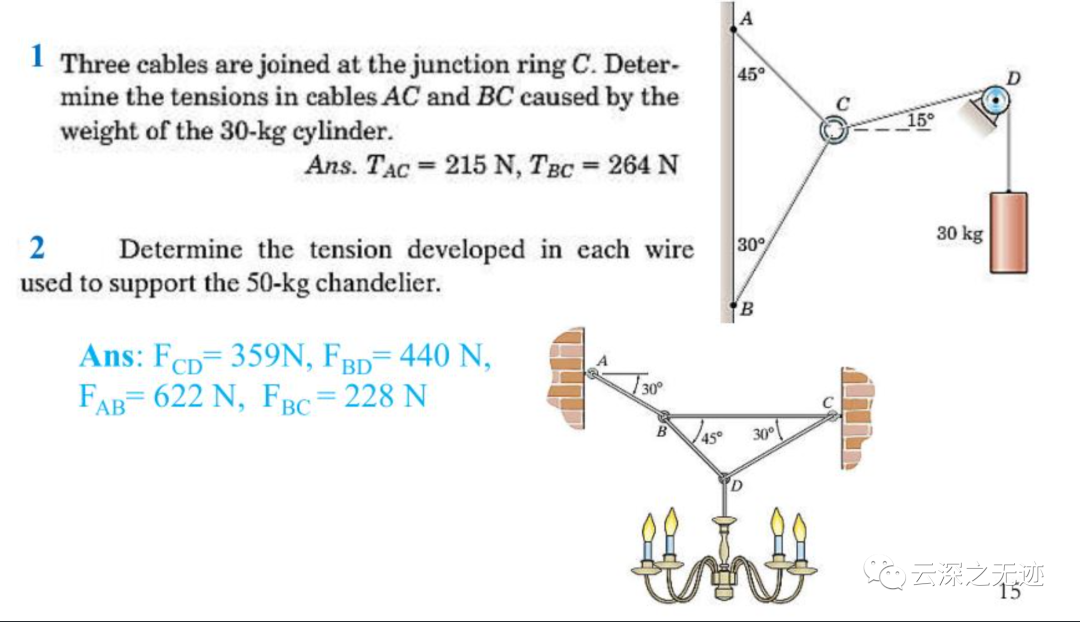
程序第一個給的例題是這個，我配錯了圖，對不起了

?解析沿矩形分量的力

(force, angle) => (force_x, force_y)，這個就是最終的結(jié)果。

因為提起角度就有兩個不同的記法，這里也做了一個角度的兼容。

Core就是一個正交分解

弧度制

我們這個圖就很完美了

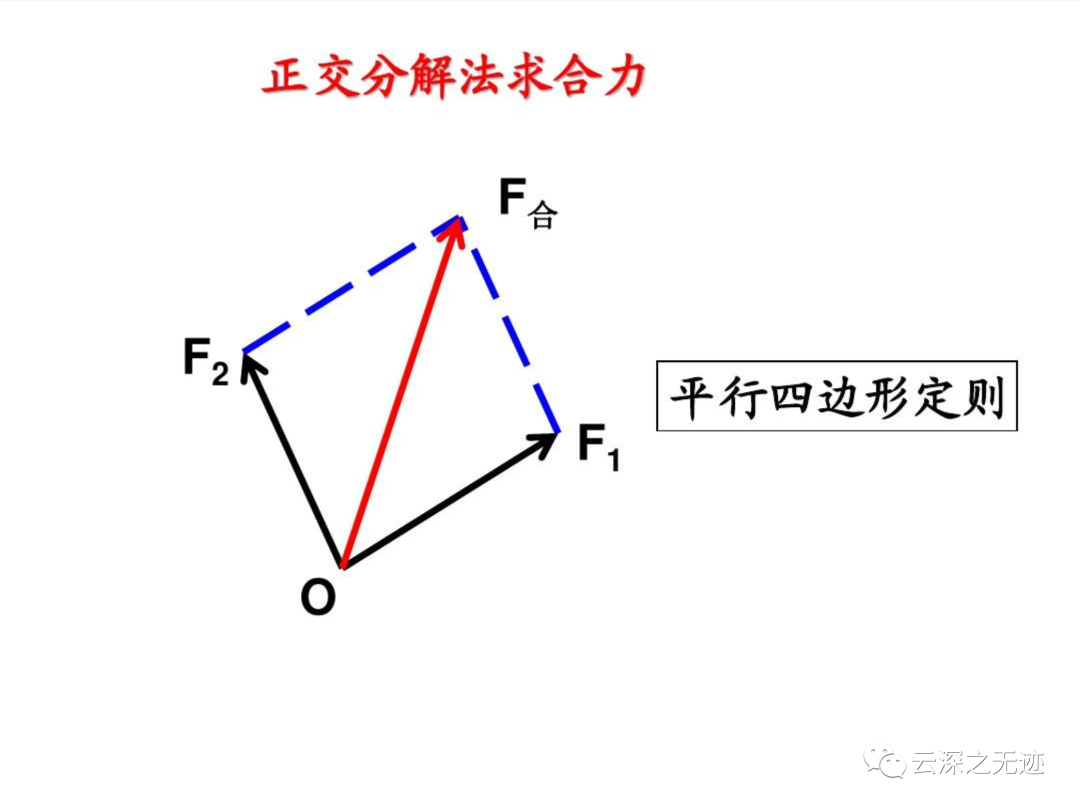
還有一個是比較泛化的正交分解

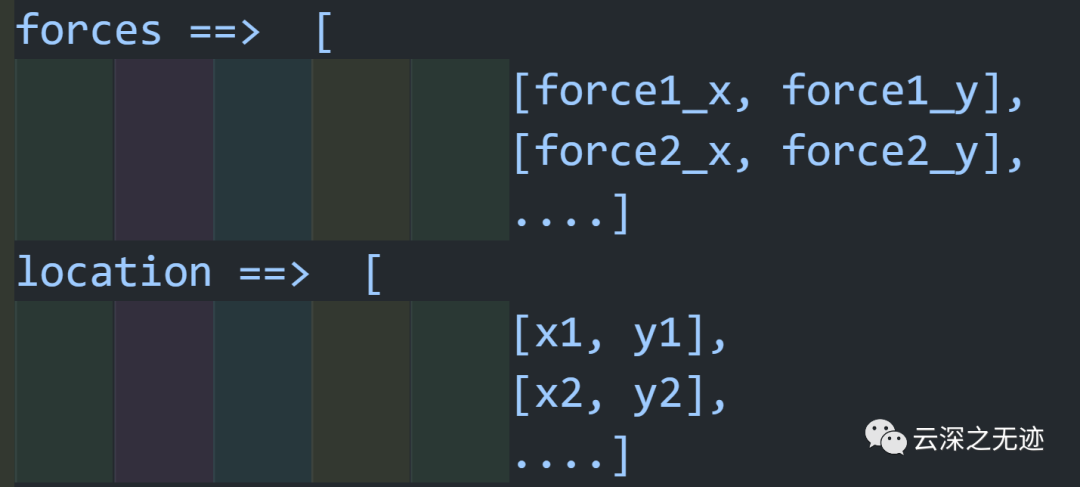
在函數(shù)的參數(shù)構(gòu)建中，分力，位置

in_static_equilibrium(force, location)

最后就會給出結(jié)果

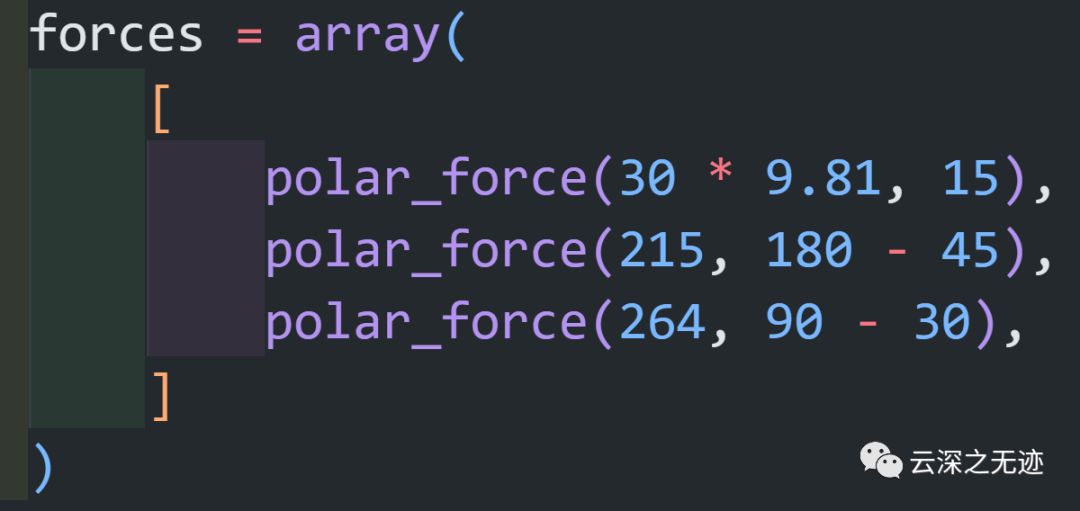
對于例題，這就是我們的分力，三組

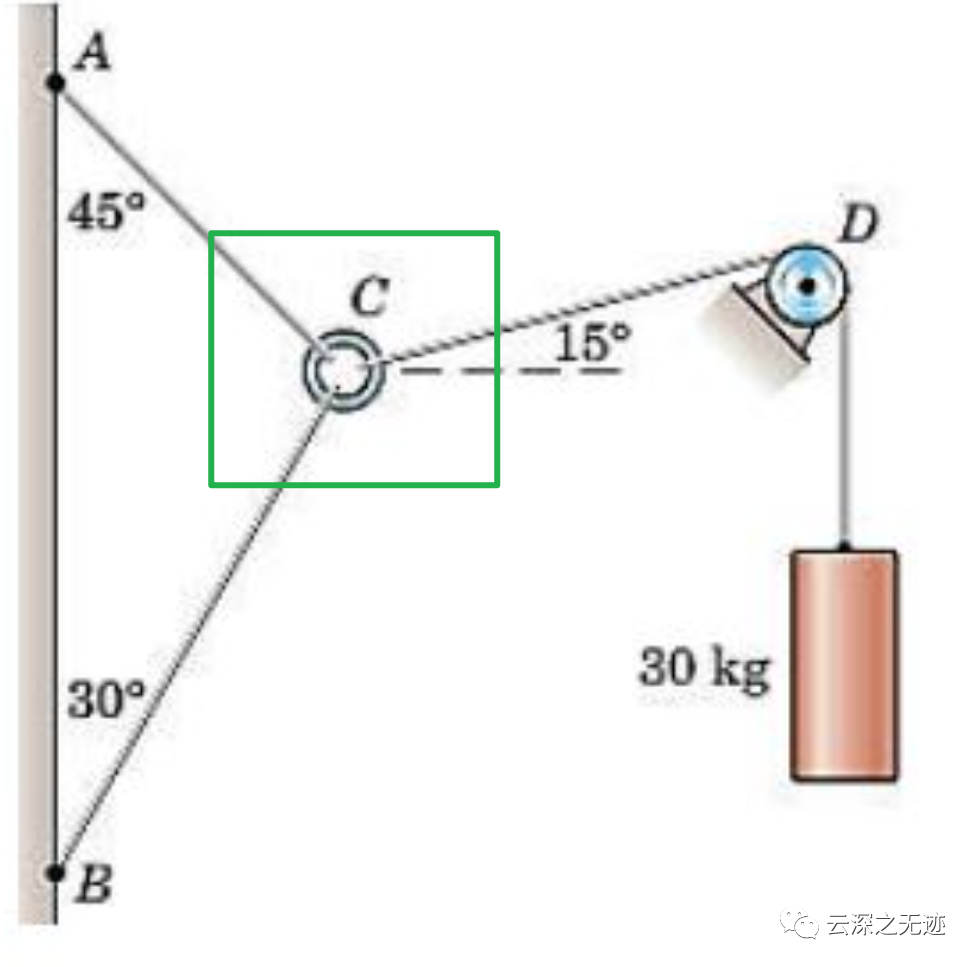
三個點在原點處的平衡情況

location = array([[0, 0], [0, 0], [0, 0]])assertin_static_equilibrium(forces,location)

這樣調(diào)用就好

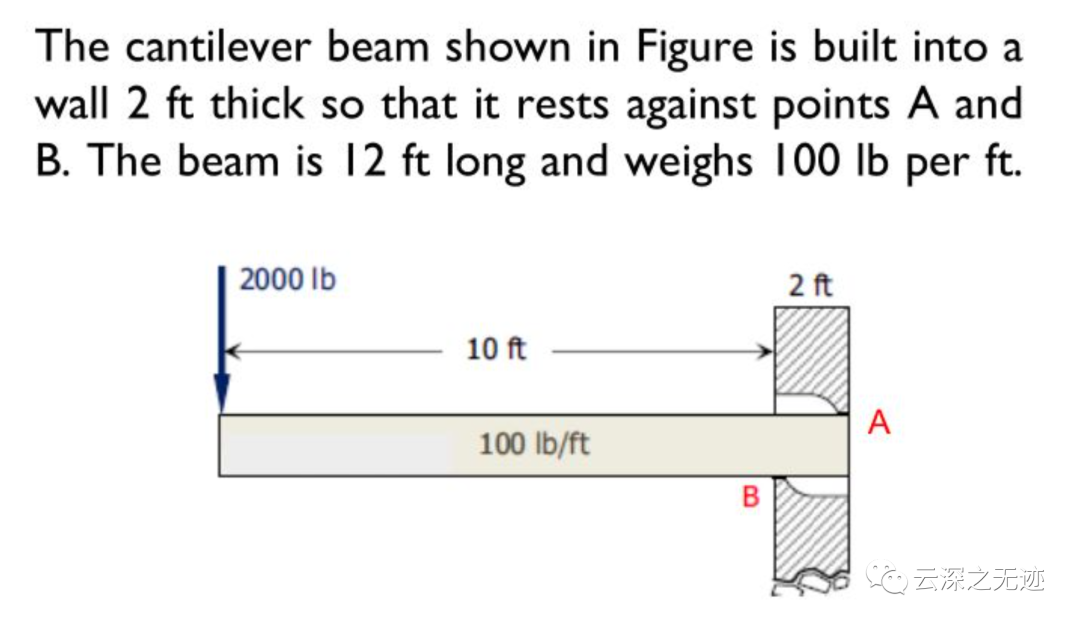
對于這個，因為角度特殊，所以力直接給出

四力，四點

import mathforce = polar_force(10, 45)math.isclose(force[0], 7.071067811865477)
True
math.isclose(force[1], 7.0710678118654755)
Truepolar_force(10, 3.14, radian_mode=True)
[-9.999987317275396,0.01592652916486828]

在Python數(shù)學(xué)模塊中，math.isclose()方法用于確定兩個浮點數(shù)的值是否接近。要使用此函數(shù)，你必須導(dǎo)入數(shù)學(xué)模塊。

用法：isclose(a, b, rel_tol = 1e-09, abs_tol 0.0)

參數(shù)：rel_tol:被視為“close”的最大差，相對于輸入值的大小

abs_tol:“close”的最大差異，與輸入值的大小無關(guān)

cross是叉積

numpy.cross

numpy.cross(a,b,axisa=-1,axisb=-1,axisc=-1,axis=None)

返回兩個（數(shù)組）向量的叉積。

a和b 的叉積是垂直于a和b的向量。如果a和b是向量的數(shù)組，則默認(rèn)情況下，向量由a和b的最后一個軸定義，并且這些軸的尺寸可以為2或3。其中a或b的尺寸為2時，則第三個分量假定輸入向量為零，并據(jù)此計算叉積。如果兩個輸入向量的尺寸均為2，則返回叉積的z分量。

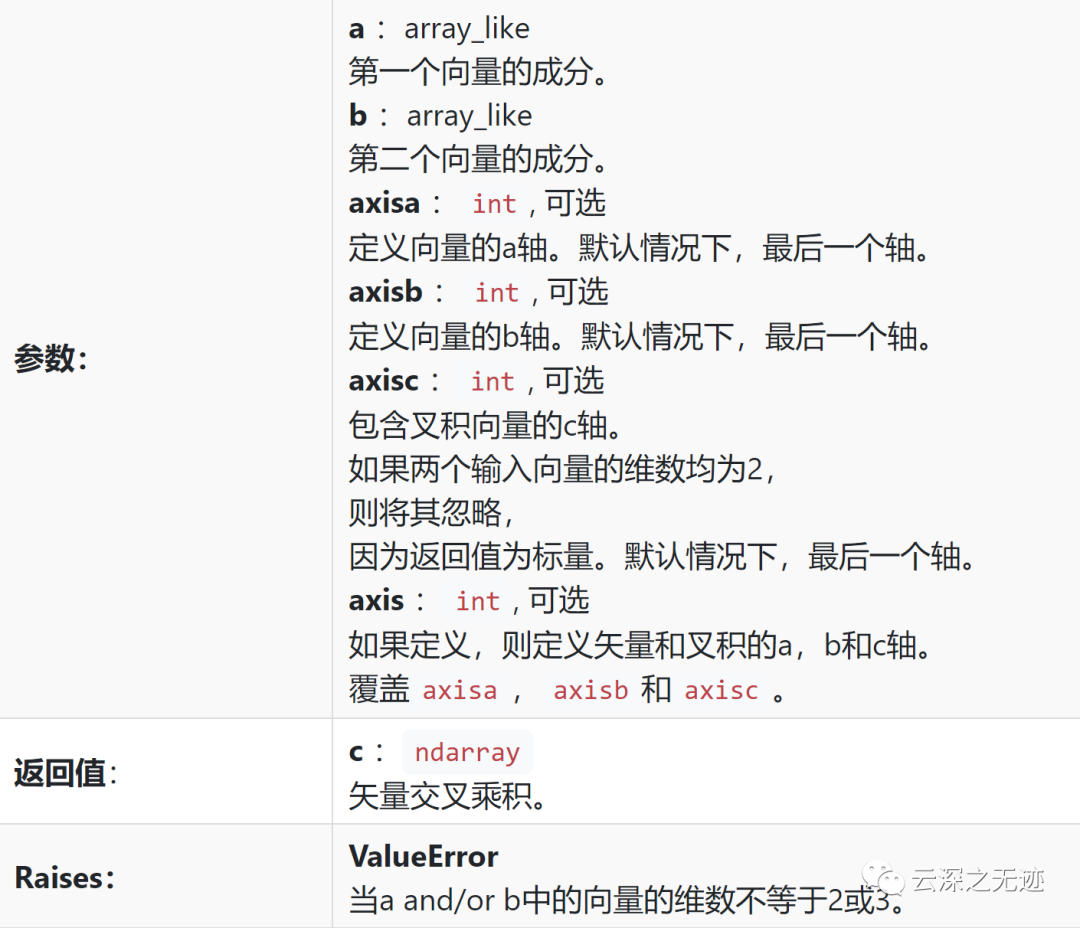
參數(shù)表

叉積來了哈~

向量積，數(shù)學(xué)中又稱外積、叉積，物理中稱矢積、叉乘，是一種在向量空間中向量的二元運算。與點積不同，它的運算結(jié)果是一個向量而不是一個標(biāo)量。并且兩個向量的叉積與這兩個向量和垂直。

a x b就是a叉b（廢話？？？）有時也用^這個符號。

向量積可以被定義為：

模長:(在這里θ表示兩向量之間的夾角（共起點的前提下）（0°≤θ≤180°），它位于這兩個矢量所定義的平面上.)

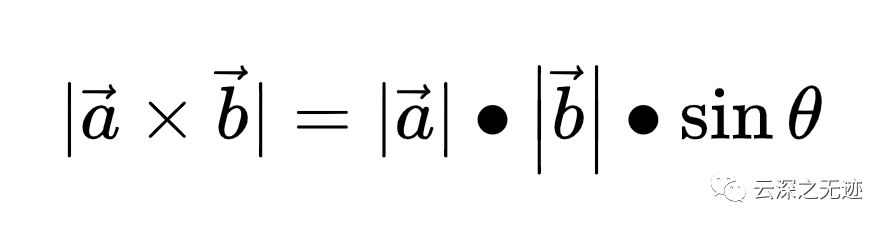
就像這樣

方向：a向量與b向量的向量積的方向與這兩個向量所在平面垂直，且遵守右手定則。（一個簡單的確定滿足“右手定則”的結(jié)果向量的方向的方法是這樣的：若坐標(biāo)系是滿足右手定則的，當(dāng)右手的四指從a以不超過180度的轉(zhuǎn)角轉(zhuǎn)向b時，豎起的大拇指指向是c的方向。）

也可以這樣定義（等效）：

向量積|c|=|a×b|=|a||b|sin

即c的長度在數(shù)值上等于以a，b，夾角為θ組成的平行四邊形的面積。

而c的方向垂直于a與b所決定的平面，c的指向按右手定則從a轉(zhuǎn)向b來確定。

平時見到的各種積：

這里可以簡單的總結(jié)一下

對于這樣的東西，一個好的可視化解釋，可以讓你記憶猶新：

叉積的長度|a×b|可以解釋成這兩個叉乘向量a，b共起點時，所構(gòu)成平行四邊形的面積。據(jù)此有：混合積[abc]=（a×b）·c可以得到以a，b，c為棱的平行六面體的體積。

在數(shù)學(xué)里面，我們給定一種運算法則后會試圖將它融入到現(xiàn)有的數(shù)學(xué)體系。所以這里給出代數(shù)規(guī)則：

1、反交換律：a×b=-b×a

2、加法的分配律：a×（b+c）=a×b+a×c。

3、與標(biāo)量乘法兼容：（ra）×b=a×（rb）=r（a×b）。

4、不滿足結(jié)合律，但滿足雅可比恒等式：a×（b×c）+b×（c×a）+c×（a×b）=0。

5、分配律，線性性和雅可比恒等式別表明：具有向量加法和叉積的R3構(gòu)成了一個李代數(shù)。

6、兩個非零向量a和b平行，當(dāng)且僅當(dāng)a×b=0。

是不是混進(jìn)來一個雅可比？？？

雅可比恒等式是橢圓函數(shù)理論中的一個著名恒等式。雅可比恒等式就是下列等式：

[X,[Y,Z]]+[Y,[Z,X]]+[Z,[X,Y]]=0

滿足雅可比恒等式的代數(shù)結(jié)構(gòu)不一定滿足反交換律。

上面的橢圓理論什么的是復(fù)變函數(shù)里面的，我只是一個土狗，不知道怎么說。

OKOK，叉積又不得不提拉格朗日公式：

（a×b）×c=b（a·c）-a（b·c）

a×（b×c）=b（a·c）-c（a·b）

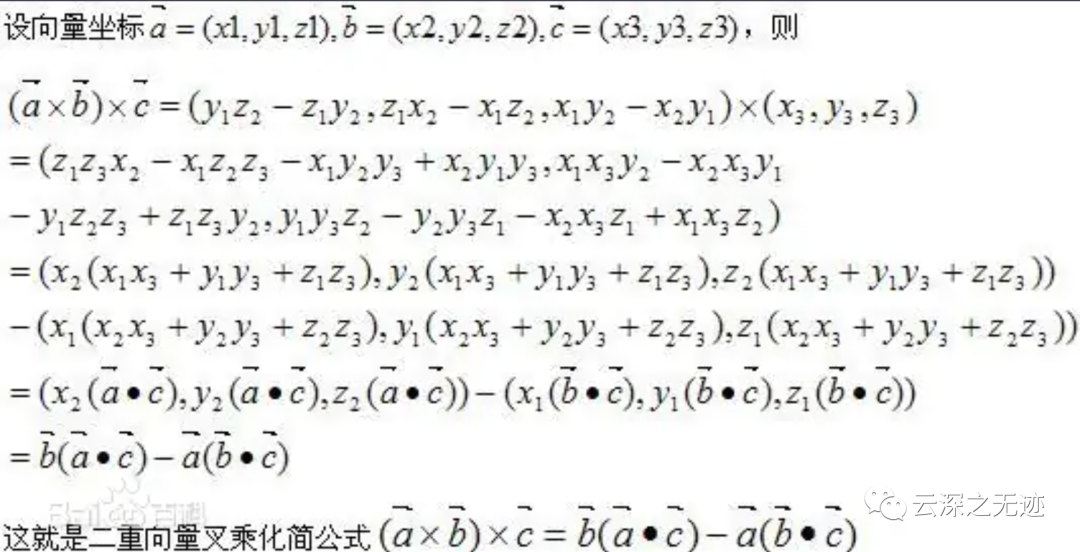
證明過程

可以簡單地記成“BAC-CAB”。這個公式在物理上簡化向量運算非常有效。等等？？？你是不是不知道上面說的是什么。

他叫：二重向量叉乘化簡公式。

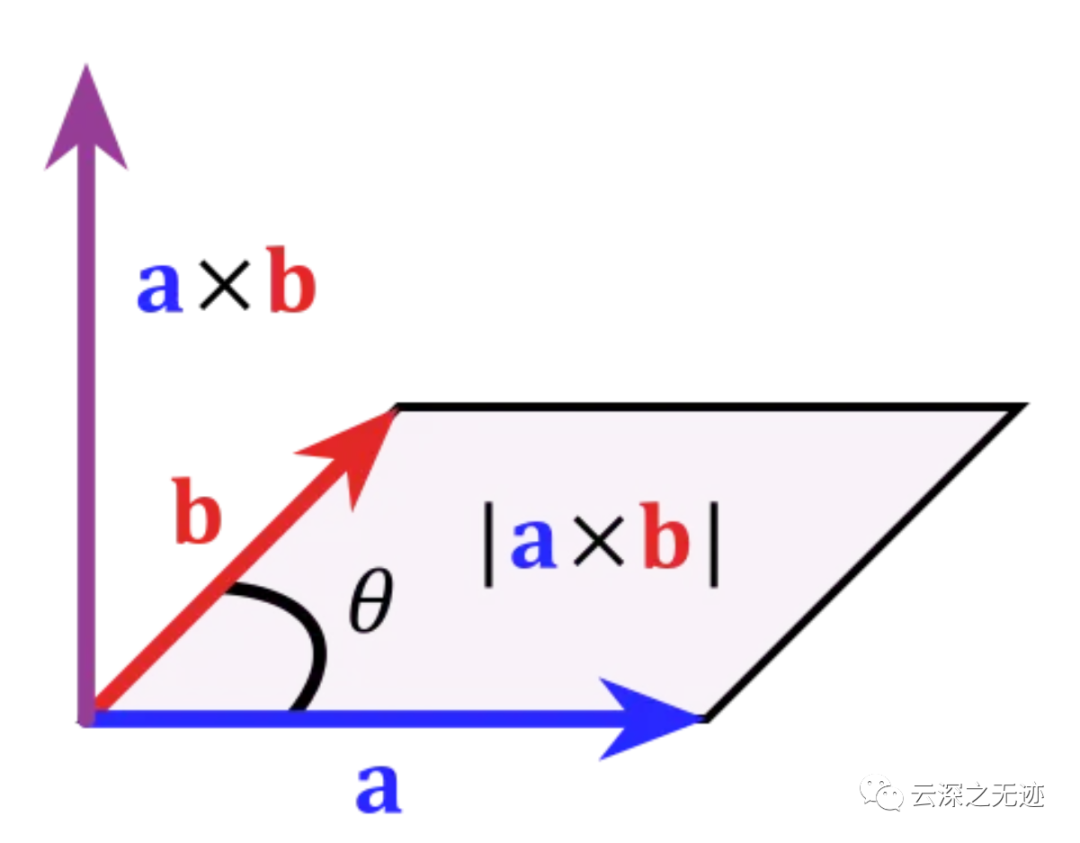
說了這么多的字，可能沒有一張圖來的快

哥倆好？不是~是叉積的方向啦！

伸出右手，將大拇指指向a，將食指指向b，中指自然彎曲，并使中指同時垂直于食指和拇指，那么此時中指所指的方向就是a×b的方向。

從這個右手定則，我們可以發(fā)現(xiàn)，兩個向量的叉積同時垂直這兩個向量，并且：

a×b=-b×a

也就是確確實實的不支持交換律。

不過既然物理這么多了，也不怕再多點：

在力的作用線的延長線或反向延長線經(jīng)過原點時，力矩為零。力矩在物理學(xué)里是指作用力使物體繞著轉(zhuǎn)動軸或支點轉(zhuǎn)動的趨向。力矩的單位是牛頓米。力矩的概念，起源于阿基米德對杠桿的研究。轉(zhuǎn)動力矩又稱為轉(zhuǎn)矩或扭矩。力矩能夠使物體改變其旋轉(zhuǎn)運動。推擠或拖拉涉及到作用力 ，而扭轉(zhuǎn)則涉及到力矩。力矩等于徑向矢量與作用力的叉積。

為什么說力矩，因為最后有叉積。

這是我們的判斷是否處于平衡狀態(tài)

因為要叉積計算，注意兩個向量的個數(shù)

這里也注意內(nèi)在，位置是矢量，分力也是矢量，所以可以計算。求完以后將值sum然后小于一個小數(shù)，證明平衡。

這里簡單的分析一下：

叉乘的模，等于兩個向量的模的乘積乘以sinθ。θ是兩個向量的夾角，如果兩個向量的模不為0，那么sinθ要等于0，也就是夾角是0°或者180°，那么兩個向量平行。

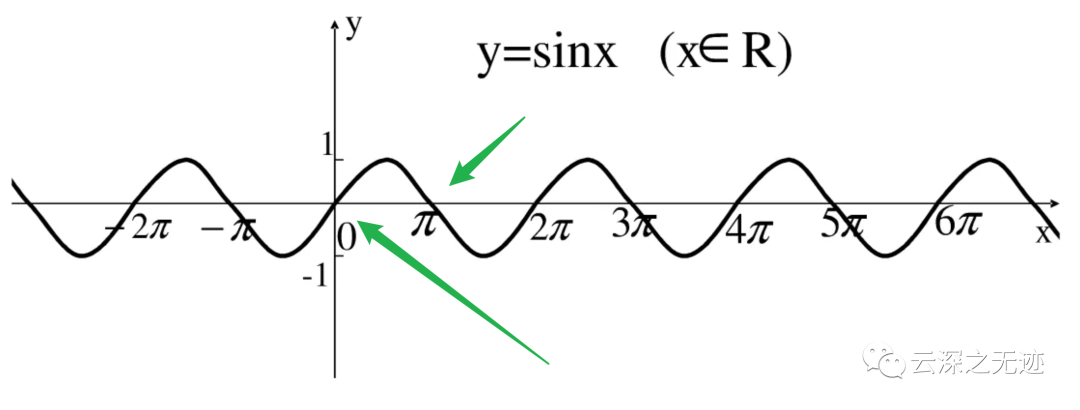
就是這些位置

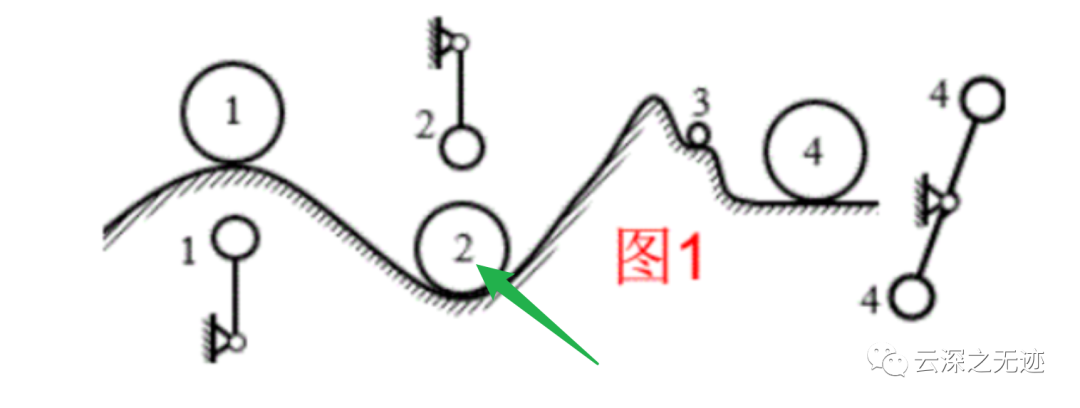
我們再分析，2是最穩(wěn)定的狀態(tài)，那么它的分力和原點叉積和越小越穩(wěn)定

這篇文章有點長了，感激你看到這里，叉積會算了嗎？靚仔