陀螺儀是一種測量物體旋轉速度的傳感器。陀螺儀的工作原理對許多工程師來說可能是神秘的。
考慮到這一點,并且受到 來自 Analog Devices 的一篇文章的啟發,本文試圖對MEMS振動陀螺儀背后的理論進行更詳細的解釋。由于全面的分析可能涉及數學密集型,我們將嘗試考慮傳感器的特殊方向,以盡可能簡化討論。
使用極坐標系定位旋轉對象
使用極坐標系可以更容易地描述旋轉物體的位置。假設,如下圖 1 所示,對象始終位于 XY 平面內。
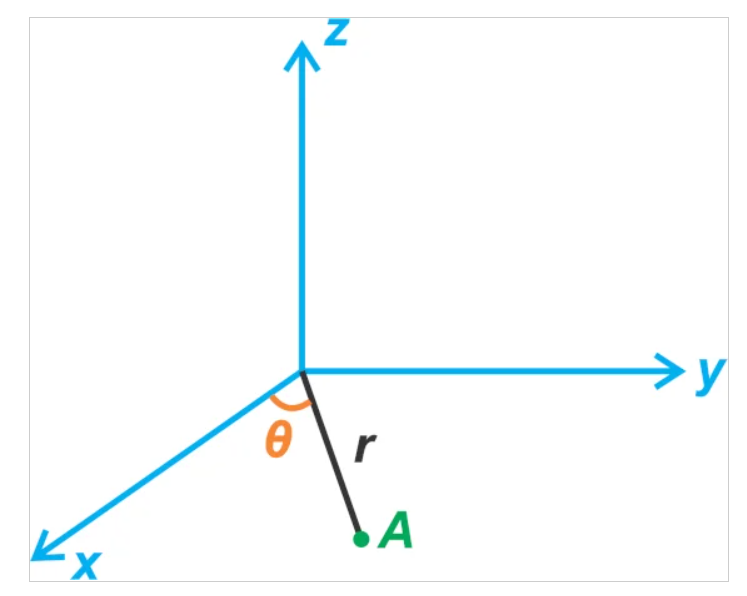
圖 1. XYZ 平面上的示例對象。
隨著 θ 的變化,點 A 圍繞 z 軸旋轉。您可能記得在數學課中,單位向量 ^rr^ 和 ^θθ^ 是為極坐標系定義的,如圖 2 所示,以唯一地指定坐標系中的一個點XY 平面。
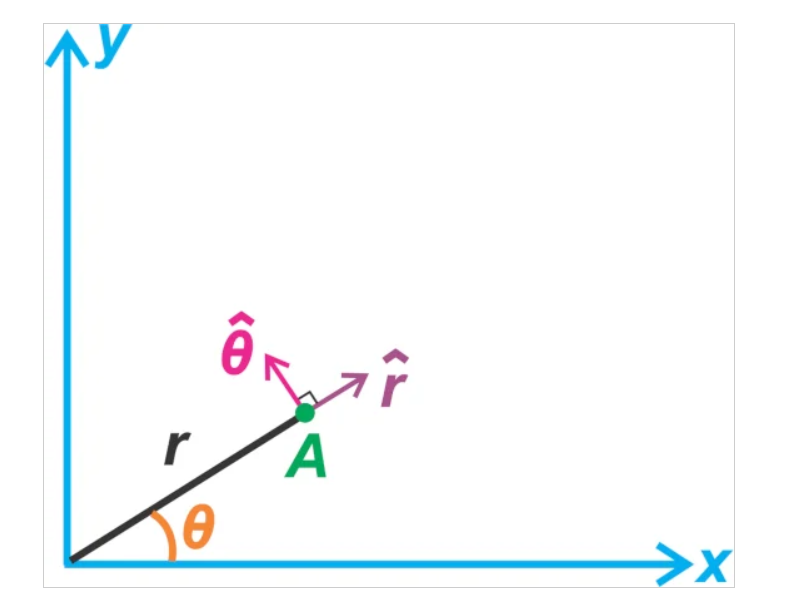
圖 2. 極坐標系示例。

第一項考慮了一個明顯的點:如果我們保持 θ 不變,我們仍然可以通過將物體與原點的距離改變 Δr 來改變物體的位置,如圖 3 所示。在這種情況下,速度應該具有徑向分量,即在$$\hat{r}$$的方向。^rr^.
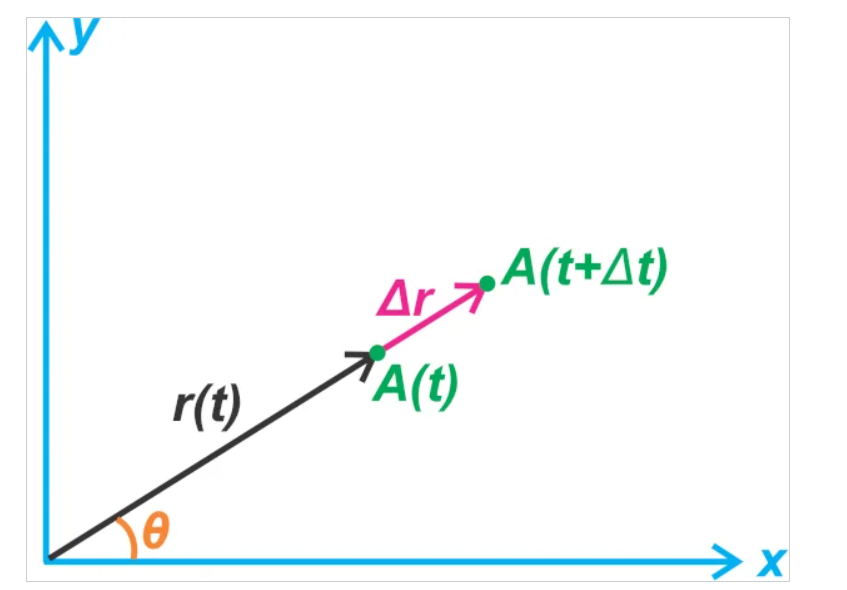
圖 3. 通過改變距離來改變物體的位置。
等式 2 中的第二項考慮了這樣一個事實:即使與原點的距離是恒定的,物體的位置也會因旋轉而改變。請記住,盡管 $$\hat{r}$$ 的長度為 1,但它的方向取決于 θ 并且可以隨時間變化。圖 4(a) 顯示了如果我們保持 r 不變并將角度增加 Δθ,則位置如何變化。^rr^長度為 1,它的方向取決于 θ 并且可以隨時間變化。圖 4(a) 顯示了如果我們保持 r 不變并將角度增加 Δθ,則位置如何變化。
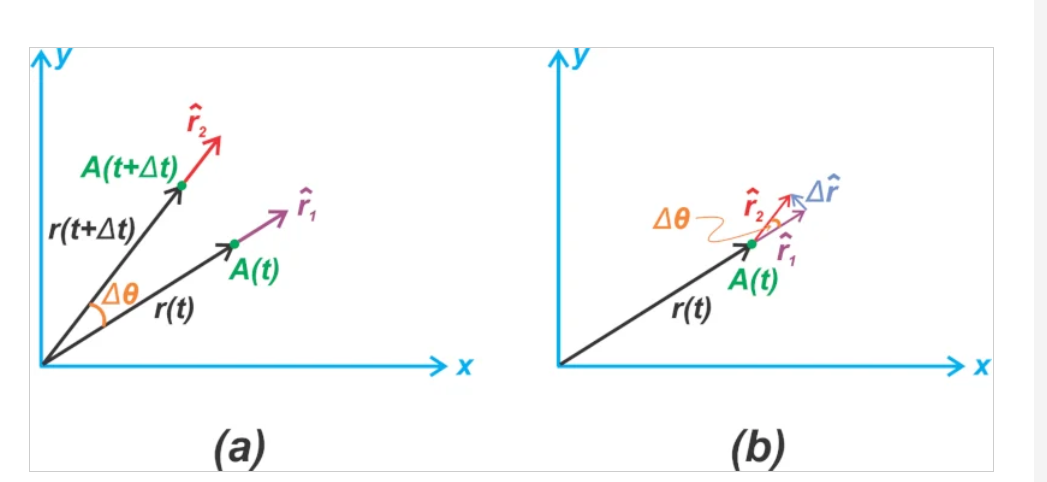
圖 4. 如果 r 為常數且角度增加 Δθ (a) 并找到該變化 (b) 時位置如何變化的示例。




VA→=drdtr^+rdθdtθ^
洞察方程式
等式 8 中的切線項是振動陀螺儀運行的關鍵。讓我們更仔細地研究一下這個術語是如何創建的。圖 5 顯示了珠子沿旋轉輪輻移動的軌跡。
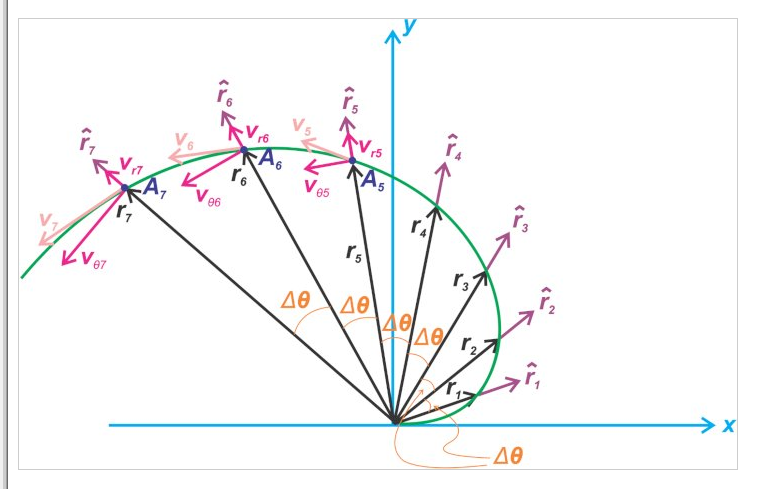
圖 5. 顯示珠沿旋轉輪輻軌跡的示例。

vθ=rdθd噸=rωvθ=rdθdt=rω
圖 5 顯示了位置 A5、A6 和 A7 的這些速度分量。在我們的示例中,徑向分量的大小是恒定的,但是切向分量呢?
由于 ? 是常數,因此速度的切向分量隨 r 增加。換句話說,當我們遠離原點時,珠子必須在給定的時間間隔和 Δθ 內移動更長的距離。通過比較連續位置向量之間的距離,您可以清楚地看到這一點。
另一個問題是由于這種現象,切向速度的變化速度有多快?
對于給定的 ?,給出加速度的切向分量的切向速度的變化率等于 r 的變化率。因此,切向加速度的一個分量由下式給出:


MEMS陀螺儀的基本結構
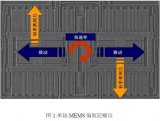
圖 6 顯示了振動陀螺儀的基本結構。
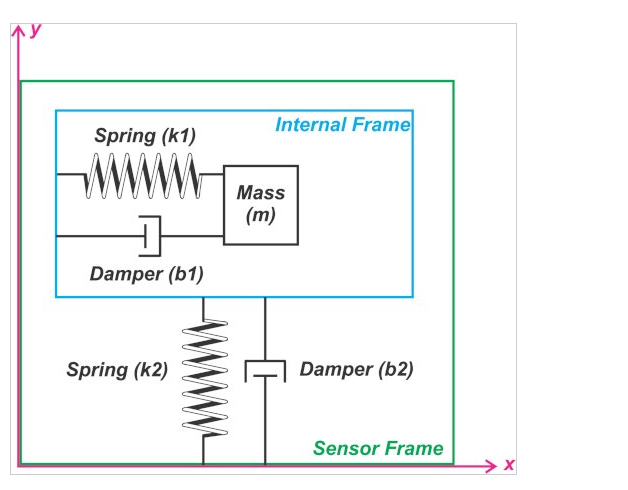
圖 6. 振動陀螺儀的示例結構。
質量 (m) 通過阻尼彈簧結構連接到“內部框架”。此外,由正反饋系統(上面未顯示)控制的致動器用于驅動質量進入諧波振蕩。如圖所示,反饋系統保證質量保持在沿 x 軸的可調節連續振蕩中。此外,內部框架通過相對于質量振蕩方向呈 90° 的第二阻尼彈簧結構連接到“傳感器框架”。當在該方向上存在力時,這種配置允許內部框架能夠在 y 軸方向上移動。
正如我們將在下一節中看到的,當傳感器繞垂直于圖中所示 XY 平面的軸旋轉時,圖 6 所示的結構可以檢測角速度。
振動陀螺儀如何工作?
假設,如圖 7 所示,陀螺儀固定在逆時針方向旋轉的平臺上。
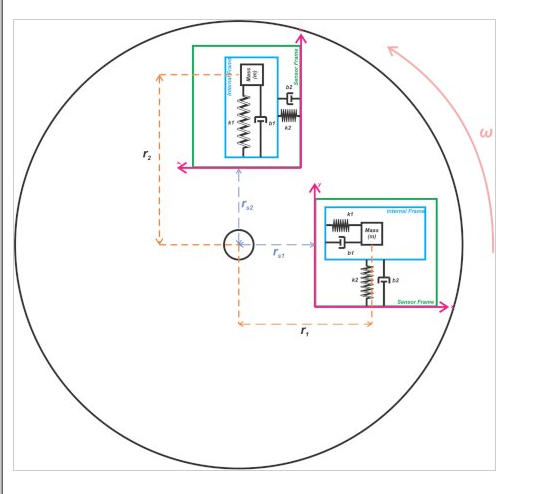
圖 7. 固定平臺上逆時針旋轉的陀螺儀。
該圖顯示了兩個不同時刻的傳感器。盡管傳感器封裝與平臺中心的距離是固定的,但我們知道質量距離從 r 1變為 r 2是由于其在傳感器框架的 x 方向上的振蕩。在此示例中,質量距離增加 r 2 》 r 1。
與圖 5 中描述的磁珠示例類似,檢測質量在傳感器 y 軸的正方向上經歷切向加速度。在 y 方向上,質量塊剛性連接到內部框架。因此,同樣的加速度也適用于內部框架。內部框架;然而,最初傾向于保持靜止,這會改變內部框架相對于傳感器框架的相對位置。
-
傳感器
+關注
關注
2561文章
52443瀏覽量
762950 -
陀螺儀
+關注
關注
44文章
827瀏覽量
99625
發布評論請先 登錄
詳解三軸陀螺儀的技術原理
中國自己的MEMS陀螺儀誕生
三軸陀螺儀是什么_三軸陀螺儀在手機上的應用
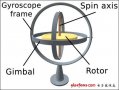
MEMS陀螺儀技術原理_三軸陀螺儀技術原理
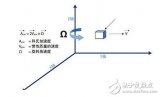
淺談MEMS陀螺儀技術 MEMS是否取代光纖陀螺儀技術
分析三軸陀螺儀的工作原理及應用
光纖陀螺儀與旋轉式陀螺儀的工作原理解析
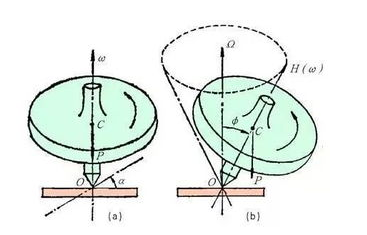
微機械陀螺儀工作原理_微機械陀螺儀的應用
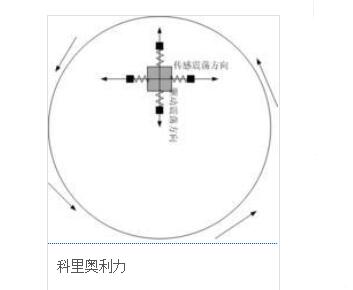
MEMS IMU/陀螺儀對準的基礎知識

什么是MEMS陀螺儀?
怎么解決陀螺儀角度漂移問題 三軸陀螺儀和六軸陀螺儀的區別
陀螺儀是什么?陀螺儀工作原理





 陀螺儀的基礎知識和結構
陀螺儀的基礎知識和結構










評論