完整的揚聲器會包括幾個部份：喇叭單體、分頻網絡、音箱這三大區塊，我們就分門別類來討論。首先就是喇叭單體，基本上來說就是將麥克風的工作原理倒過來，以電氣訊號輸入在磁力系統里音圈上的線圈，線圈會隨著訊號產生磁性變化，而帶動音圈在磁力系統中以聲音的波形運動。音圈再推動喇叭單體的振膜或音盆，以推動空氣產生音波，聲音就這樣發出來了。

說來確實并不困難，不過要將電氣訊號盡可能地依原來應有的波形、響應等低失真的情況發出聲音就是另外一回事了。音頻范圍由低頻（20Hz）到高頻（18kHz）超過了十個八度音程，單一喇叭單體要能涵蓋這個音頻范圍，在音量方面就會受到結構的限制。不過現在全音域單體技術成熟發達，市面上已經有不少性能還不錯的全音域單體供貨銷售了。

當然要建構能發出大音量高帶寬的揚聲系統，就需要將不同音域配置給不同特性的單體，諸如低頻域（300Hz以下）配置給低音單體、中頻域（300Hz-2500Hz）給中音單體，高頻域（2500Hz以上）給高音單體分別發音，整合成完整的音域。低頻因為需要推動大量的空氣，所以需要最大的振膜/音盆；中音域需要推動的空氣量較少，因此音盆口徑與單體尺寸也更小更輕；而高音域只需要推動最少的空氣，因此高音單體也是振膜與體型最輕小的。

基本上來說，單體音盆/振膜口徑愈大，質量就愈重能推動愈多空氣，但也具備更大的慣性所以反應的速度會降低，因此適合更低的頻率；反之單體的振膜口徑愈小質量愈輕的，就具備更快的反應速度，能發出更高的頻率，但相對能推動的空氣量就有限。這也是為何市面上稍有體積的揚聲器，都會配置多音路與多個單體整合發音。

當然這樣的話就要將擴大機的電氣訊號分出高低音路甚或中音路，也就是所謂的「分頻」。一般說來揚聲系統的分頻方式有兩種做法，最主流的方式就是以被動分頻網絡，將擴大機的訊號分出頻率范圍不同的音路出來。而被動分頻網絡說穿了就是被動的電感、電容與電阻所構成的「濾波器」，將該音路的音域范圍以外的頻段予以濾除，而只剩下所需的頻段能夠通過。所以揚聲器統設有幾個音路，也就會有幾組濾波網絡來構成分頻網絡，分別驅動負責不同音域的單體。

另外一種做法是「電子分音」，是由訊號還在前級輸出的階段，就輸送至電子分音器，分出所需頻段的各音域，不過采用的是主動式的電子分音電路，一般說來分頻效果會比起被動分頻網絡要來得更好。但分頻出來的不同音路就需要個別不同的擴大機去推動各音路的單體，因此會大幅提升揚聲系統的成本；通常電子分音都是由比較大型的揚聲系統所采用（還有會另文介紹的專業鑒聽揚聲器）。

最后這些不同音路的單體當然要裝置起來成為一組完整的揚聲系統，不過還需要進一步考慮的，是單體前后往復震動推動空氣發出聲音，其前后的聲音是「反相」的，如果不進一步處理的話，會在聆聽空間中產生彼此抵消的效應，因此需要「裝箱」將單體后方發出的「背波」做進一步的處理。一般說來每只單體都會有獨立的空間來處理背波，中高音若是單體的體積較小，單體出廠時就會建置密封的背腔預先處理。

所以揚聲器音箱最主要還是針對某些口徑較大的中音與低音單體設計。目前揚聲器音箱設計有兩種主流方式：密閉式與開放式，開放式的主流是低音反射式，也就是讓音箱的低音腔室容量與反射導管的口徑與長度經過計算，與單體的低頻特性調諧以產生更大量（適量）的低頻表現。但密閉式的音箱容積依然要經過考慮單體特性的計算，讓低頻可以得到最低頻率的延伸。

不過開放式的音箱并不只有低音反射的設計方式，還有諸如雙單體多氣室的Isobarik形式或是傳輸線（將音箱內部隔成長導管的形態以延伸低頻頻率）等諸多方式。音箱的材質與結構上也有諸多設計以強化其結構避免產生共振影響音質，最主流的材質就是所謂的「中密度纖維板」（MDF），此種材料有價格合宜、加工容易以及效果理想的的諸多特性。當然也有揚聲器廠家采用金屬或特殊材料設計/建構音箱，以取得更佳的特性與效果。

以上就是典型揚聲器的構成要素，當然在技術上還有其他不同的設計會脫離上述的范疇，例如「電漿/離子高音」式采用放電的方式驅動空氣；「靜電揚聲器」是采用電極/電場驅動薄膜來推動空氣發音，根本沒有音箱結構。要將電能轉為聲能確實還有諸多其他方式，不過目前技術最成熟也是最主流的做法，依然是以電磁系統為原理的傳統單體、再與音箱結構整合的傳統揚聲器。

01 物理神經網絡

??看到最近在 Nature 雜志上發表的一篇文章 Deep Physical Neural Networks Trained with Backpropogation［1］ 介紹了利用多層非線性物理系統構建深度學習網絡，并通過反向隨機梯度下降完成系統訓練方法的確令人驚訝、毀人三觀。

??你敢想象利用幾只揚聲器，或者幾只場效應管就可以組成深度物理神經網絡（Physical Neural Networks），完成圖像分類？分類效果比起傳統的數字神經網絡也不遜色。對于MNIST手寫體數字識別也可達到97%以上。（見下面基于四通道雙諧波信號發生器（SHG）方案）

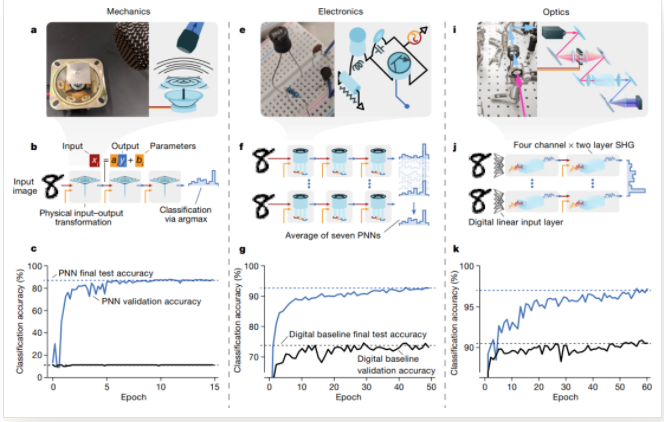
▲ 圖1 分別基于機械系統、電子線路、光學系統構建的P物理神經網絡

??這類建構在物理系統而非數字處理器之上的神經網絡目標是在推理速度和能效方面超過傳統數字計算機，構建智能傳感器和高效網絡推理。

??猜測大多數人和我一樣，第一看到這個文章都會有疑問：這類常見到的揚聲器、三極管、光學透鏡怎么就能夠像深度學習網絡那樣完成學習訓練和推理的呢？特別是這其中都是一些常見到的物理系統，這里面并沒有包含什么量子計算機、神經計算機之類結構。

??文章包含的工作很多（原文PDF有60多頁），我還沒有看完，不過文章一開始把為什么物理神經網絡能夠實現人工神經網絡算法的原理還是講的比較明白。傳統的深度學習可以分解若干網絡層的級聯計算，每一層的計算包括輸入數據（Input）、網絡參數（Parameters），它們經過融合后經過神經元非線性傳遞函數形成網絡的輸出（Output）。

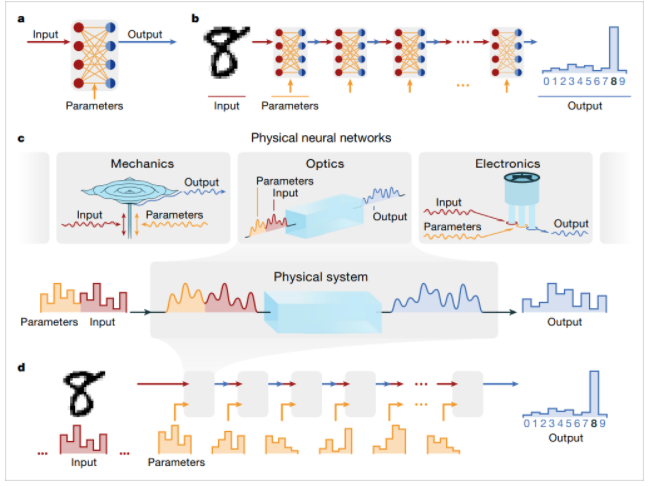
▲ 圖2 人工神經網絡（ANN）與物理神經網絡（PNN） 之間的聯系

??物理神經網絡也是分成若干層的級聯，比如若干個揚聲器，每個揚聲器是一層神經網絡。輸入信號是揚聲器的輸入電壓；網絡參數則是一組可以控制的電壓信號，比如持續時間，幅值可以改變的信號，它們與輸入信號通過（疊加、串聯等）合并后送入揚聲器，揚聲器的輸出聲音再經過麥克風采集形成網絡的輸出。

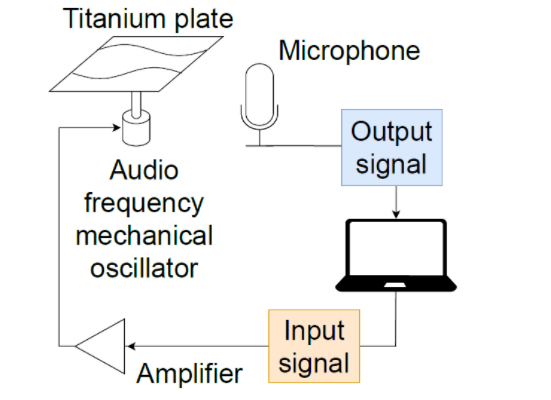
▲ 圖1.3 由揚聲器組成的一層神經網絡結構圖

??在由晶體管組成的放大電路、光學倍頻器（SHG）組成的系中，對于輸入信號，網絡參數以及它們的融合方法根據各子系統特點有所不同。

??比如在下圖中，網絡參數實際上就是一段長度和幅值不同的直流信號，嵌入在輸入變化的信號中（A），經過三極管電路之后形成輸出（B），輸入信號和網絡參數融合部分進行展開與歸一化（C）形成網絡輸出信號。

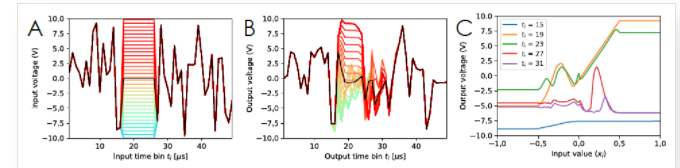
▲ 圖3 在三極管電路中輸入信號網絡參數信號（幅值可控一段直流電平）的串聯，以及對應的電路輸出信號

??盡管現在對于網絡如何進行訓練，如何進行工作的細節還有待進一步的了解，但文章所展示關于深度神經網絡算法的本質令人耳目一新。利用了系統輸入輸出之間的非線性把輸入信號與網絡信號進行融合完成信息的處理，所以文章所舉例的三個系統（揚聲器、三極管電路、二次倍頻光學系統）都應該不是線性時不變系統。

??下面，我們拋開物理神經網絡算法，先看看論文中的這三個系統的特點。

02 非線性系統

??在大學本科階段所學習的“信號與系統”、“自動控制理論”中所討論的原理和方法基本上都是針對于線性時不變系統，因此判斷一個系統是否是線性時不變是應用這些理論第一步需要做的事情。

??在前面Nature 論文中所提到的三個物理系統（機械、電子、光學）是否都滿足線性時不變呢？

2.1 三極管電路

??文章中三極管電路最簡單，同樣它的非線性也最為明顯。

??電路包含有四個元器件：電阻、電感、電容以及場效應三極管。其中電阻、電感、電容都是線性元器件，只有場效應三極管是一個非線性器件。它的漏極飽和電流與柵極電壓之間呈現平方關系。所以該電子系統是一個非線性系統。

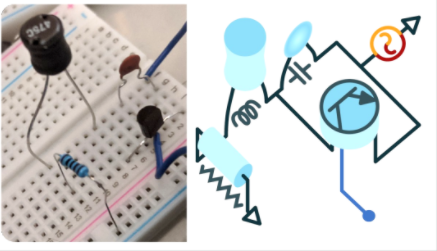
▲ 圖2.1.1 三極管電路

2.2 二次諧波產生系統（SHG）

??二次諧波產生系統 是一個光學系統，也是文章舉例中最復雜的系統。

??對于SHG（Second-Harmonic Generation）光學系統我不是很熟悉，通過 檢索相應文獻［2］ 可以了解到它的基本原理。它利用了 一些特殊的分子物理狀態可以將輸入光學信號的頻率進行倍頻，產生對應的二次諧波信號。

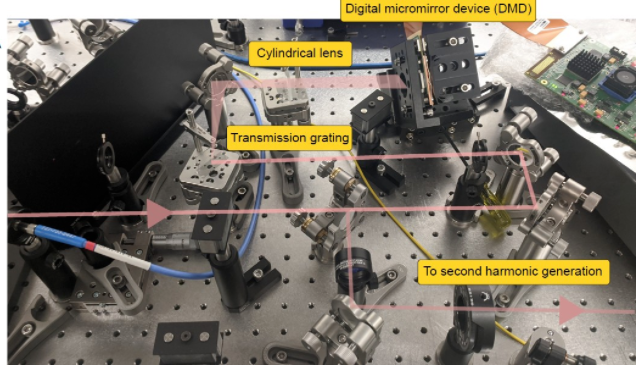
▲ 圖2.2.1 二次諧波產生系統

??對于這類你不熟悉的物理系統，那么該如何判斷它 是否屬于線性時不變系統呢？

??在這里我們需要利用線性時不變系統的一個特性：線性時不變系統不會產生新的頻率信號。

??雖然它可以改變輸入信號中不同頻率分量的幅度和相位，但不會有新的頻率分量產生。SHG光學系統是將輸入光譜中所有頻率分量都進行倍頻，產生了新的倍頻分量，因此它不屬于線性時不變系統。

??因此，倍頻是該系統能夠用于完成物理神經系統的關鍵，一個線性時不變光學系統是無法構建物理神經網絡的。

2.3 揚聲器

??文章舉例的三個系統中，就數揚聲器機械振動系統最令人感到撲朔迷離。系統分為揚聲器、音頻功放、麥克風組成。其中揚聲器需要進行改裝。

??他們把動圈式喇叭的振動膜和防塵罩拆除，露出音頻線圈，在上面使用膠水粘上一個金屬螺釘，再固定一個3.2cm×3.2cm見方，1mm厚的金屬鉭制作的金屬片。讀到此，你會覺得他們這通騷操作屬于脫了褲子放屁，故弄玄虛。

▲ 圖2.3.1 利用揚聲器制作的機械振蕩系統

??原以為他們這么改裝應該是想在喇叭機械系統中融入非線性環節，但在音圈（Sound Coil）上增加的金屬螺釘和鉭片好像僅僅是增加了喇叭線圈慣性質量，對于其中高頻振蕩進行壓制，起到一個低頻濾波的作用。因此該系統仍然屬于一個線性時不變系統。

??下面是論文補充材料中給出的揚聲器輸入電壓信號，麥克風錄音信號以及信號降采樣的數字信號。可以看到麥克風錄制的音頻信號的確是對輸入信號的低通平滑濾波。

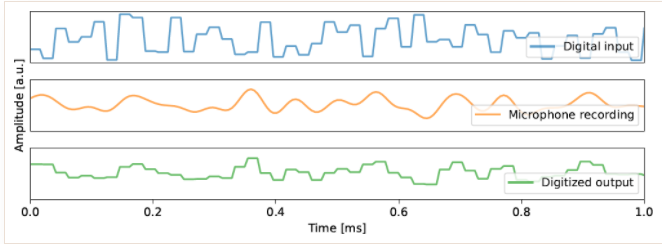
▲ 圖2.3.2 揚聲器的輸入信號、麥克風錄音信號以及降采樣數字信號

??下圖是文章中給出的輸入隨機信號中嵌入了幅度可控一段直流信號（相當于網絡參數），施加在揚聲器上之后，麥克風采集到的音頻信號。最后一張圖上可以看到在不同時刻對應的輸出信號與輸入信號之間呈現線性關系。

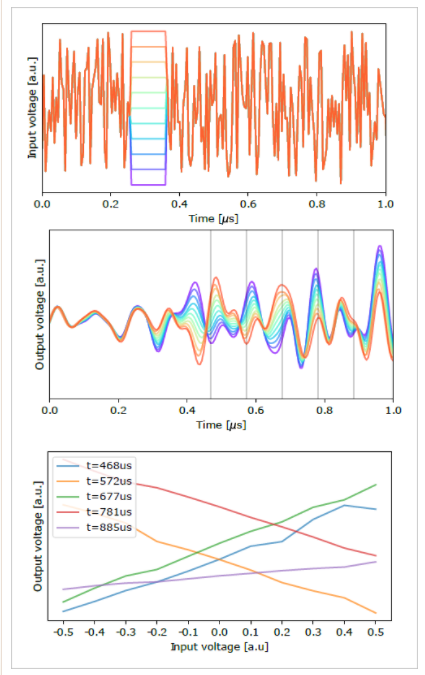
▲ 圖2.3.3 輸入隨機噪聲加上可控直流信號片段噪聲的輸出信號

??那么問題來了：這個系統中的非線性環節到底在哪兒呢？

??現在能夠想到的就是其中麥克風信號進行降采樣可能會改變系統的線性時不變特性，類似于卷積神經網中的 Pooling 層的作用。

※ 總 結 ※

??來自于康納爾大學的這篇研究論文給出了 一個利用物理系統實現深層網絡學習和推理的框架。本文對于文章舉例的三個系統不屬于線性時不變系統進行分析。除了其中SHG系統比較復雜之外，其它兩個系統（三極管、揚聲器）是如此的簡便，吸引人去進行搭建系統，測試一下相應的性能性能。

參考資料

［1］Deep Physical Neural Networks Trained with Backpropogation： https://www.nature.com/articles/s41586-021-04223-6.pdf［2］檢索相應文獻： https://www.sciencedirect.com/topics/chemistry/second-harmonic-generation