人工神經(jīng)網(wǎng)絡(luò) （ ANN ）是 人工智能（ AI ） 技術(shù)的基本構(gòu)件。人工神經(jīng)網(wǎng)絡(luò)是 machine-learning 模型的基礎(chǔ)；它們模擬的學(xué)習(xí)過程與人腦相同。簡言之，人工神經(jīng)網(wǎng)絡(luò)賦予機(jī)器完成特定任務(wù)的類似于人的性能（以及更高性能）的能力。本文旨在為數(shù)據(jù)科學(xué)家提供基本的高級知識，以了解在訓(xùn)練 ANN 時(shí)調(diào)用的函數(shù)和方法所涉及的低級操作。

作為數(shù)據(jù)科學(xué)家，我們的目標(biāo)是通過暴露數(shù)據(jù)中的模式來解決業(yè)務(wù)問題。通常，這是通過使用機(jī)器學(xué)習(xí)算法來識別模式和以模型表示的預(yù)測來完成的。為特定用例選擇正確的模型，并適當(dāng)?shù)卣{(diào)整參數(shù)，需要徹底了解問題和底層算法。對問題域和算法的理解是需要考慮的，以確保我們正確使用模型，并正確解釋結(jié)果。

本文介紹并解釋了梯度下降和反向傳播算法。這些算法有助于 ANN 從數(shù)據(jù)集中學(xué)習(xí)，特別是在涉及數(shù)據(jù)點(diǎn)和神經(jīng)網(wǎng)絡(luò)預(yù)測的操作導(dǎo)致網(wǎng)絡(luò)參數(shù)值發(fā)生修改的情況下。

建立直覺

在我們進(jìn)入這篇文章的技術(shù)細(xì)節(jié)之前，讓我們先看看人類是如何學(xué)習(xí)的。

人類大腦的學(xué)習(xí)過程是復(fù)雜的，研究幾乎沒有觸及人類學(xué)習(xí)的表面。然而，我們所知道的很少的東西對構(gòu)建模型是有價(jià)值和有幫助的。與機(jī)器不同，人類不需要大量數(shù)據(jù)來理解如何解決問題或做出邏輯預(yù)測；相反，我們從經(jīng)驗(yàn)和錯(cuò)誤中學(xué)習(xí)。

人類通過突觸可塑性的過程學(xué)習(xí)。突觸可塑性是一個(gè)術(shù)語，用來描述獲得新信息后新的神經(jīng)連接是如何形成和加強(qiáng)的。就像我們在經(jīng)歷新事件時(shí)大腦中的連接得到加強(qiáng)和形成一樣，我們通過計(jì)算神經(jīng)網(wǎng)絡(luò)預(yù)測的誤差來訓(xùn)練人工神經(jīng)網(wǎng)絡(luò)，并根據(jù)這些誤差加強(qiáng)或削弱神經(jīng)元之間的內(nèi)部連接。

梯度下降

梯度下降是一種標(biāo)準(zhǔn)的優(yōu)化算法。它通常是第一個(gè)用于訓(xùn)練機(jī)器學(xué)習(xí)的優(yōu)化算法。讓我們剖析“梯度下降”這個(gè)術(shù)語，以便更好地理解它與機(jī)器學(xué)習(xí)算法的關(guān)系。

坡度是對直線或曲線的陡度進(jìn)行量化的測量。從數(shù)學(xué)上講，它詳細(xì)說明了直線上升或下降的方向。下降是向下的動(dòng)作。因此，梯度下降算法根據(jù)這些短語的兩個(gè)簡單定義量化向下運(yùn)動(dòng)。

為了訓(xùn)練機(jī)器學(xué)習(xí)算法，您需要努力識別網(wǎng)絡(luò)中的權(quán)重和偏差，以幫助您解決所考慮的問題。例如，您可能有分類問題。查看圖像時(shí)，需要確定圖像是貓還是狗。為了建立模型，您需要使用正確標(biāo)記的貓和狗圖像數(shù)據(jù)樣本來訓(xùn)練算法。

雖然上面描述的示例是分類，但問題可能是定位或檢測。盡管如此， well 神經(jīng)網(wǎng)絡(luò)在問題上的表現(xiàn)被建模為一個(gè)函數(shù)，更具體地說，是一個(gè)成本函數(shù)；成本或有時(shí)被稱為損失函數(shù)的東西衡量模型的錯(cuò)誤程度。成本函數(shù)的偏導(dǎo)數(shù)影響最終模型的權(quán)重和選擇的偏差。

梯度下降是一種算法，有助于搜索參數(shù)值，使代價(jià)函數(shù)最小化，以達(dá)到局部最小或最優(yōu)精度。

神經(jīng)網(wǎng)絡(luò)中的代價(jià)函數(shù)、梯度下降和反向傳播

神經(jīng)網(wǎng)絡(luò)令人印象深刻。同樣令人印象深刻的是，計(jì)算程序能夠區(qū)分圖像和圖像中的對象，而無需明確告知要檢測的特征。

將神經(jīng)網(wǎng)絡(luò)視為接受輸入（數(shù)據(jù)）以產(chǎn)生輸出預(yù)測的函數(shù)是有幫助的。這個(gè)函數(shù)的變量是神經(jīng)元的參數(shù)或權(quán)重。

因此，解決交給神經(jīng)網(wǎng)絡(luò)的任務(wù)的關(guān)鍵任務(wù)是以近似或最好地代表數(shù)據(jù)集的方式調(diào)整權(quán)重和偏差的值。

下圖描繪了一個(gè)接收輸入（ X ）的簡單神經(jīng)網(wǎng)絡(luò)1十、2十、3十、N） ，這些輸入被轉(zhuǎn)發(fā)到包含權(quán)重（ W ）的層內(nèi)的神經(jīng)元1W2W3WN） 。輸入和權(quán)重經(jīng)過乘法運(yùn)算，結(jié)果通過加法器（）相加，激活函數(shù)調(diào)節(jié)層的最終輸出。

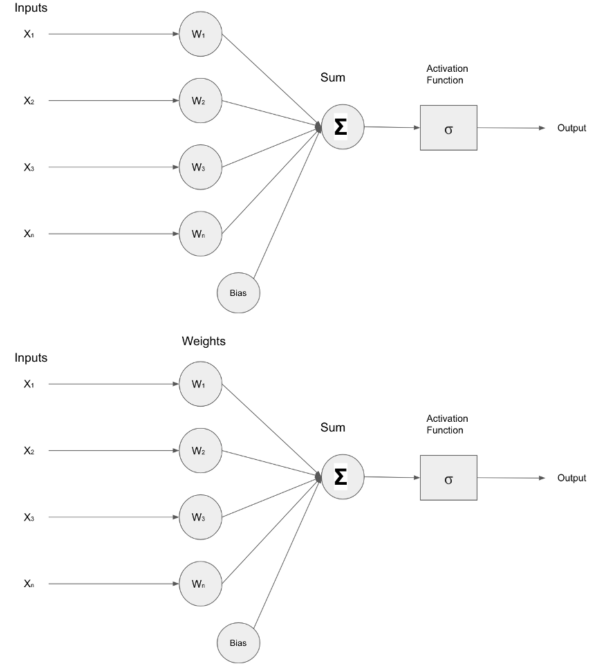
圖 1 ：作者創(chuàng)建的淺層神經(jīng)網(wǎng)絡(luò)的圖像。

為了評估神經(jīng)網(wǎng)絡(luò)的性能，需要一種機(jī)制來量化神經(jīng)網(wǎng)絡(luò)預(yù)測和實(shí)際數(shù)據(jù)樣本值之間的差異或差距，從而計(jì)算出影響神經(jīng)網(wǎng)絡(luò)內(nèi)權(quán)重和偏差修改的因素。

cost function 簡化了神經(jīng)網(wǎng)絡(luò)預(yù)測值和數(shù)據(jù)樣本實(shí)際值之間的誤差差距。

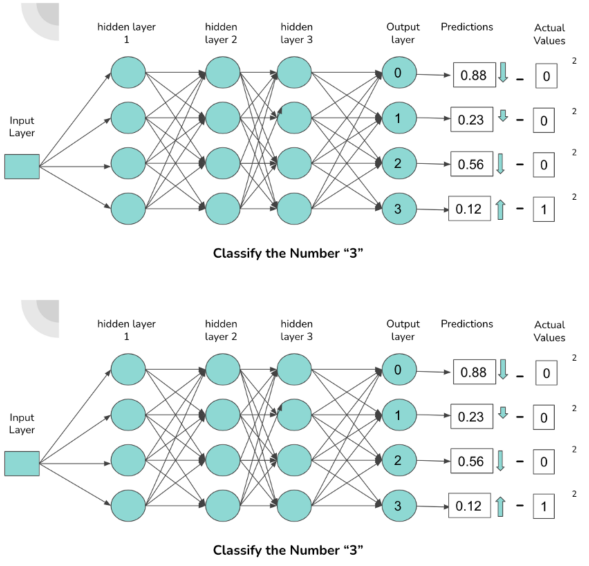
圖 2 ：描述的神經(jīng)網(wǎng)絡(luò)內(nèi)部連接和預(yù)測。

上圖展示了一個(gè)由密集連接的神經(jīng)元組成的簡單神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)，它對包含數(shù)字 0-3 的圖像進(jìn)行分類。輸出層中的每個(gè)神經(jīng)元對應(yīng)一個(gè)數(shù)字。與神經(jīng)元連接的激活程度越高，神經(jīng)元輸出的概率就越高。概率對應(yīng)于通過網(wǎng)絡(luò)前饋的數(shù)字與激活的神經(jīng)元相關(guān)聯(lián)的可能性。

當(dāng)一個(gè)“ 3 ”通過網(wǎng)絡(luò)前饋時(shí)，我們期望負(fù)責(zé)分類“ 3 ”的連接（由圖中的箭頭表示）具有更高的激活度，這導(dǎo)致與數(shù)字“ 3 ”相關(guān)的輸出神經(jīng)元的概率更高。

神經(jīng)元的激活有幾個(gè)因素，即偏差、權(quán)重和前一層的激活。為了使神經(jīng)網(wǎng)絡(luò)在特定數(shù)據(jù)集上獲得最佳性能，必須對這些指定的組件進(jìn)行迭代修改。

通過利用“均方誤差”等成本函數(shù)，我們獲得了與網(wǎng)絡(luò)誤差有關(guān)的信息，用于通過網(wǎng)絡(luò)的權(quán)重和偏差向后傳播更新。

為完整起見，以下是機(jī)器學(xué)習(xí)中使用的成本函數(shù)示例：

均方誤差

范疇交叉熵

二元交叉熵

對數(shù)損失

我們已經(jīng)介紹了如何通過測量網(wǎng)絡(luò)預(yù)測的技術(shù)來提高神經(jīng)網(wǎng)絡(luò)的性能。本文的其余內(nèi)容主要關(guān)注梯度下降、反向傳播和成本函數(shù)之間的關(guān)系。

圖 3 中的圖像顯示了繪制在 x 軸和 y 軸上的成本函數(shù)，該函數(shù)的參數(shù)空間中包含值。讓我們來看看神經(jīng)網(wǎng)絡(luò)是如何學(xué)習(xí)的，它將代價(jià)函數(shù)可視化為一個(gè)不均勻的曲面，繪制在一個(gè)圖上，在可能的權(quán)重/參數(shù)值的參數(shù)空間內(nèi)。

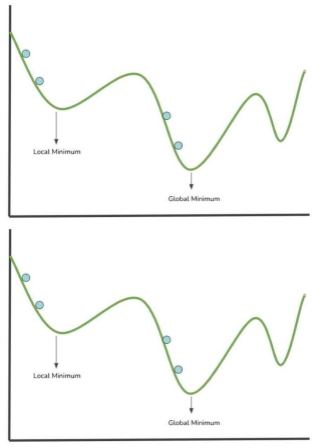
圖 3 ：可視化的梯度下降。

上圖中的藍(lán)色點(diǎn)表示搜索局部最小值的步驟（將參數(shù)值計(jì)算到成本函數(shù)中）。建模成本函數(shù)的最低點(diǎn)對應(yīng)于導(dǎo)致成本函數(shù)最低值的權(quán)重值的位置。代價(jià)函數(shù)越小，神經(jīng)網(wǎng)絡(luò)的性能越好。因此，可以根據(jù)收集的信息修改網(wǎng)絡(luò)的權(quán)重。

梯度下降法是一種算法，用于引導(dǎo)在每一步中選擇的成對值朝著最小值移動(dòng)。

局部最小值：成本函數(shù)指定范圍或扇區(qū)內(nèi)的最小參數(shù)值。

全局最小值：這是整個(gè)成本函數(shù)域內(nèi)的最小參數(shù)值。

梯度下降算法通過計(jì)算可微函數(shù)的梯度并沿梯度的相反方向移動(dòng)，指導(dǎo)搜索以局部/全局最小值最小化函數(shù)的值。

反向傳播是一種機(jī)制，通過這種機(jī)制，可以反復(fù)調(diào)整影響神經(jīng)元輸出的組件（偏差、權(quán)重、激活），以降低成本函數(shù)。在神經(jīng)網(wǎng)絡(luò)的結(jié)構(gòu)中，神經(jīng)元的輸入，包括與前一層神經(jīng)元的所有先前連接，決定了它的輸出。

反向傳播涉及的關(guān)鍵數(shù)學(xué)過程是導(dǎo)數(shù)的計(jì)算。反向傳播操作計(jì)算成本函數(shù)相對于權(quán)重、偏差和前一層激活的偏導(dǎo)數(shù)，以確定哪些值會(huì)影響成本函數(shù)的梯度。

通過計(jì)算梯度使代價(jià)函數(shù)最小化，得到局部極小值。在每個(gè)迭代或訓(xùn)練步驟中，網(wǎng)絡(luò)中的權(quán)重通過計(jì)算的梯度以及 learning rate 進(jìn)行更新，該梯度控制對權(quán)重值的修改因子。在神經(jīng)網(wǎng)絡(luò)的訓(xùn)練階段，每個(gè)步驟都要重復(fù)這個(gè)過程。理想情況下，目標(biāo)是在每一步之后更接近局部最小值。

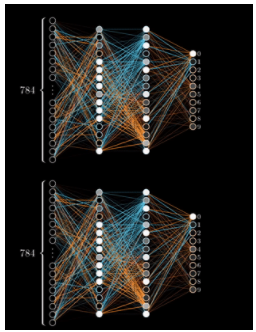
圖 4 ：錯(cuò)誤的反向傳播（反向傳播）。

“反向傳播”這個(gè)名字來源于進(jìn)程的字面意思，即“錯(cuò)誤的反向傳播”。梯度的偏導(dǎo)數(shù)量化了誤差。通過在網(wǎng)絡(luò)中向后傳播誤差，最后一層（距離輸出層最近的層）梯度的偏導(dǎo)數(shù)用于計(jì)算第二層到最后一層的梯度。

誤差在各層中傳播，并利用當(dāng)前層中前一層的梯度偏導(dǎo)數(shù)，直到到達(dá)網(wǎng)絡(luò)中的第一層（距離輸入層最近的層）。

總結(jié)

這只是梯度下降主題的入門。有一個(gè)數(shù)學(xué)和微積分的世界與梯度下降相關(guān)。

TensorFlow 、 SciKit-Learn 、 PyTorch 等軟件包通常會(huì)抽象出實(shí)現(xiàn)訓(xùn)練和優(yōu)化算法的復(fù)雜性。然而，這并不能免除數(shù)據(jù)科學(xué)家和 ML 從業(yè)者理解這些智能“黑匣子”背后發(fā)生的事情的要求。

關(guān)于作者

Richmond Alake 是一名機(jī)器學(xué)習(xí)和計(jì)算機(jī)視覺工程師，他與多家初創(chuàng)公司和公司合作，整合深度學(xué)習(xí)模型，以解決商業(yè)應(yīng)用中的計(jì)算機(jī)視覺任務(wù)。

審核編輯：郭婷