圖神經網絡圖解指南圖神經網絡或簡稱 GNN 是用于圖數據的深度學習 (DL) 模型。這些年來它們變得很熱。這種趨勢在 DL 領域并不新鮮:每年我們都會看到一個新模型的脫穎而出,它要么在基準測試中顯示最先進的結果,要么是一個全新的機制/框架到已經使用的模型中(但是你閱讀論文時會感到很簡單)。這種反思讓我們質疑這種專門用于圖形數據的新模型存在的原因。
為什么我們需要GNN ?圖表無處不在:圖表數據非常豐富,我認為這是展示我們每天產生或消費的材料最自然、最靈活的方式。從大多數公司和Facebook或Twitter等社交網絡中使用的關系數據庫,到科學和文學中連接知識創造的引文圖表,我們不需要費力地列舉一系列圖表數據的例子。甚至圖像也可以被看作是圖表,因為它們的網格結構。
模型能夠捕獲圖中所有可能的信息:正如我們所見,圖數據無處不在,并且采用具有特征向量的互連節點的形式。是的,我們可以使用一些多層感知器模型來解決我們的下游任務,但是我們將失去圖拓撲為我們提供的連接。
至于卷積神經網絡,它們的機制專用于圖的一種特殊情況:網格結構的輸入,其中節點完全連接而沒有稀疏性。話雖如此,唯一剩下的解決方案是一個模型,它可以建立在兩個給出的信息之上:節點的特征和我們圖中的局部結構,這可以減輕我們的下游任務;
這就是 GNN 所做的。GNN 訓練哪些任務?既然我們已經適度地證明了這些模型的存在,我們將揭示它們的用法。事實上,我們可以在很多任務上訓練 GNN:大圖中的節點分類(根據用戶的屬性和關系對社交網絡中的用戶進行細分),或全圖分類(對藥物應用的蛋白質結構進行分類)。
除了分類之外,回歸問題還可以在圖數據之上制定,不僅適用于節點,也適用于邊。總而言之,圖神經網絡的應用是無窮無盡的,取決于用戶的目標和他們擁有的數據類型。為簡單起見,我們將專注于唯一圖中的節點分類任務,我們嘗試將以特征向量為首的節點圖子集映射到一組預定義的類別/類。
該問題假設存在一個訓練集,其中我們有一組標記的節點,并且圖中的所有節點都有一個我們注意到 x 的特定特征向量。我們的目標是預測驗證集中特征節點的標簽。
GNN的本質現在我們已經設置了我們的問題,是時候了解 GNN 模型將如何訓練以輸出未標記節點的類。事實上,我們希望我們的模型不僅要使用我們節點的特征向量,還要利用我們處理的圖結構。使 GNN 獨一無二的最后一條語句必須包含在某個假設中,該假設聲明相鄰節點傾向于共享相同的標簽。
GNN通過使用消息傳遞形式化來整合這一點,本文將進一步討論這一概念。我們將介紹一些我們將在后面考慮的瓶頸。上面說的非常的抽象,現在讓我們看看 GNN 是如何構建的。事實上,GNN 模型包含一系列通過更新的節點表示進行通信的層(每一層為每個節點輸出一個嵌入向量,然后將其用作下一層的輸入以在其上構建)。
我們模型的目的是構建這些嵌入(對于每個節點),集成節點的初始特征向量和圍繞它們的局部圖結構的信息。一旦我們有了很好的嵌入,我們將經典的 Softmax 層提供給這些嵌入以輸出相關類。
為了構建這些嵌入,GNN層使用了一種稱為消息傳遞的簡單機制,它幫助圖節點與它們的鄰居交換信息,從而一層接一層地更新它們的嵌入向量。
消息傳遞框架
這一切都從一些節點開始,向量 x 描述它們的屬性,然后每個節點通過置換等變函數(均值、最大值、最小值……)從其鄰居節點收集其他特征向量。換句話說,一個對節點排序不敏感的函數。這個操作叫做聚合,它輸出一個消息向量。
第二步是Update函數,節點將從它的鄰居(消息向量)收集到的信息與它自己的信息(特征向量)結合起來,構造一個新的向量h: embedded。該聚合和更新函數的實例化在不同的論文中有所不同。您可以參考GCN[1]、GraphSage[2]、GAT[3]或其他,但消息傳遞的思想保持不變。
這個框架背后的直覺是什么?好吧,我們希望我們節點的新嵌入能夠考慮到本地圖結構,這就是我們從鄰居節點聚合信息的原因。通過這樣做,人們可以直觀地預見聚合后的一組鄰居節點將具有更相似的表示,這將減輕我們最終的分類任務。在我們的第一個假設(鄰居節點傾向于共享相同的標簽)的情況下,所有這些都是成立的。
GNN 中的層組合
現在我們已經了解了消息傳遞的主要機制,是時候了解層在 GNN 上下文中的含義了。回想上一節,每個節點使用來自其鄰居的信息來更新其嵌入,因此自然擴展是使用來自其鄰居(或第二跳鄰居)的鄰居的信息來增加其感受野并變得更加了解 圖結構。這就是我們 GNN 模型的第二層。我們可以通過聚合來自 N 跳鄰居的信息將其推廣到 N 層。
在這一點上,您對 GNN 的工作原理有了一個高層次的了解,并且您可能能夠發現為什么這種形式主義會出現問題。首先,在深度學習的背景下談論 GNN 假設存在深度(許多層)。
這意味著節點將可以訪問來自距離較遠且可能與它們不相似的節點的信息。一方面,消息傳遞形式主義試圖軟化鄰居節點之間的距離(平滑),以便稍后簡化我們的分類。另一方面,它可以通過使我們所有的節點嵌入相似來在另一個方向上工作,因此我們將無法對未標記的節點進行分類(過度平滑)。在下一節中,我將嘗試解釋什么是平滑和過度平滑,我們將平滑作為增加 GNN 層的自然效果進行討論,我們將了解為什么它會成為一個問題。
我還將嘗試對其進行量化(從而使其可跟蹤),并在此量化的基礎上使用已發表論文中關于此問題的解決方案來解決它。
GNN 中的過度平滑問題
雖然消息傳遞機制幫助我們利用封裝在圖形結構中的信息,但如果結合 GNN 深度,它可能會引入一些限制。換句話說,我們對更具表現力和更了解圖結構的模型的追求(通過添加更多層,以便節點可以有一個大的感受野)可以轉化為一個模型,該模型對待節點都一樣(節點表示收斂到不可區分的向量[4])。
這種平滑現象既不是錯誤也不是特例,而是 GNN 的基本性質,我們的目標是緩解它。為什么會發生過度平滑?消息傳遞框架使用了前面介紹的兩個主要函數 Aggregate 和 Update,它們從鄰居那里收集特征向量并將它們與節點自己的特征結合起來更新它們的表示。此操作的工作方式使交互節點(在此過程中)具有非常相似的表示。我們將嘗試在我們模型的第一層中說明這一點,以說明為什么會發生平滑,然后添加更多層以顯示這種表示平滑如何隨層增加。
注意:過度平滑表現為節點嵌入之間的相似性。所以我們使用顏色,其中不同的顏色意味著向量嵌入的不同。此外,在我們的示例中,為了簡單起見,我們將僅更新突出顯示的 4 個節點。
正如您在第一層中看到的,節點可以訪問單跳鄰居。例如,您還可以觀察到,節點 2 和節點 3 幾乎可以訪問相同的信息,因為它們相互鏈接并具有共同的鄰居,唯一的區別是它們的最后一個鄰居(紫色和黃色)。我們可以預測它們的嵌入會略有相似。對于節點 1 和節點 4,它們彼此交互但具有不同的鄰居。所以我們可以預測他們的新嵌入會有所不同。我們通過為每個節點分配新的嵌入來更新我們的圖,然后移動到第二層并執行相同的過程。
在我們 GNN 的第二層,節點 1,4 和 2,3 的計算圖分別幾乎相同。我們可能期望我們為這些節點更新的新嵌入將更加相似,即使對于以第一層的方式“幸存”的節點 1 和節點 4 現在也將具有相似的嵌入,因為額外的層使他們可以訪問更多 圖的部分,增加了訪問相同節點的可能性。
這個簡化的例子展示了過度平滑是 GNN 深度的結果。公平地說,這與真實案例相去甚遠,但它仍然提供了這種現象發生背后的原因。為什么這真的是一個問題?現在我們了解了為什么會發生過度平滑,以及為什么它是設計好的,這是 GNN 層組合的影響,是時候強調我們為什么應該關心它,并激勵解決方案來克服它。
首先,學習嵌入的目標是最后將它們提供給分類器,以預測它們的標簽。考慮到這種過度平滑的效果,我們最終會為沒有相同標簽的節點得到類似的嵌入,這將導致錯誤標記它們。有人可能認為減少層數會降低過度平滑的效果。是的,但這意味著在復雜結構數據的情況下不利用多跳信息,因此不會提高我們的最終任務性能。
示例:為了強調最后一句,我將用一個在現實生活中經常出現的例子來說明。想象一下,我們正在處理一個具有數千個節點的社交網絡圖。一些新用戶剛剛登錄該平臺并訂閱了他們朋友的個人資料。我們的目標是找到主題建議來填充他們的提要。
考慮到這個假想的社交網絡,在我們的GNN模型中只使用1或2層,我們將只知道我們的用戶關心連接的話題,但我們錯過了其他多樣化的話題,他可能會喜歡他的朋友的互動。綜上所述,過度平滑作為一個問題,我們遇到了一個低效率模型和一個更有深度但在節點表示方面更缺乏表現力的模型之間的權衡。
我們如何量化它?現在我們已經明確表示過度平滑是一個問題并且我們應該關心它,我們必須對其進行量化,以便我們可以在訓練 GNN 模型時對其進行跟蹤。不僅如此,量化還將為我們提供一個指標,通過將其作為正則化項添加到我們的目標函數中(或不。。。。。。),用作數值懲罰。根據我最近的閱讀,很多論文都處理了 GNN 中的過度平滑問題,他們都提出了一個度量來量化它,以證明他們對這個問題的假設并驗證他們的解決方案。
我從處理這個問題的兩篇不同論文中選擇了兩個指標。
MAD 和 MADGap [5]
Deli Chen 等人引入了兩個量化指標 MAD 和 MADGap,來衡量圖節點表示的平滑度和過度平滑度。一方面,MAD 計算圖中節點表示(嵌入)之間的平均平均距離,并使用它來表明平滑是向 GNN 模型添加更多層的自然效果。基于此度量,他們將其擴展到 MADGap,該度量度量不同類別節點之間表示的相似性。這種概括是建立在主要假設之上的,即在節點交互時,它們可以訪問來自同一類的節點的重要信息,或者通過與來自其他類的節點交互來獲取噪聲。
在這篇文章中引起我興趣的是作者對建立消息傳遞形式的主要假設的質疑方式(鄰居節點可能有類似的標簽)。事實上,他們的測量MADGap不僅僅是一個過度平滑的測量,而是一個相對于我們的節點收集的信號的信息噪聲比的測量。因此,觀察到這個比例一層接著一層地減小,就證明了圖拓撲與下游任務目標之間的不一致。
群距離比 [6]
Kaixiong Zhou 等人引入了另一個應變前向度量,但與 MADGap 具有相同的目標,即組距離比。該指標計算兩個平均距離,然后計算它們的比率。我們首先將節點放在相對于它們的標簽的特定組中。然后,為了構建我們的比率的提名者,我們計算每兩組節點之間的成對距離,然后對所得距離求平均值。至于分母,我們計算每個組的平均距離,然后計算平均值。
比例小意味著嵌入不同分組的節點之間的平均距離較小,因此我們可能會在分組的嵌入方面進行混合,這就是過平滑的證明。
我們的目標是保持一個高的組距離比,以在節點的嵌入方面有不同的類別,這將簡化我們的下游任務。
有解決方案來克服過度平滑嗎?
一個直接的監管規則?現在我們已經量化了過度平滑問題,你可能會認為我們的工作被終止了,在我們的損失目標中添加這個度量作為一個規則就足夠了。剩下的問題是,在我們的訓練會話的每次迭代中計算這些度量(上面提到的)可能會耗費計算成本,因為我們需要訪問我們的圖中的所有訓練節點,然后進行一些距離計算,處理二次縮放的節點對(C(2,n) = n * (n -1) / 2 = O(n2))一個間接的解決方案?
因此,所有討論過平滑問題的論文都考慮用其他更容易實現和對過平滑有影響的間接解決方案來克服這個計算問題。我們不會廣泛討論這些解決方案,但您將在下面找到其中一些參考資料。至于我們的例子,我們將討論Kaixiong Zhou 等人提出的可微群歸一化[6]。
DGN將節點分組,并對其進行獨立歸一化,輸出新的下一層嵌入矩陣。這個額外的層是用來優化前面定義的組距離比或Rgroup。實際上,在一個組內嵌入節點的歸一化使得它們的嵌入非常相似(減少了Rgroup的分子),而這些使用可訓練參數的縮放和移動使得來自不同組的嵌入不同(增加了Rgroup的分子)。
為什么有效?第一次看論文,沒看到加入這個歸一化層和優化Rgrou比之間的聯系,后來我觀察到這一層一方面使用了一個可訓練的分配矩陣,因此它有來自我們的損失函數,因此指導將完美情況下的節點分配給它們的真實類。
另一方面,我們還有平移和縮放參數,它們也由我們的損失函數引導。那些用于將一組嵌入到另一組的不同嵌入的參數因此有助于下游任務。
總結
這篇文章可能很長,但它只觸及了圖神經網絡及其問題的表面,我試圖從 GNN 的小探索開始,并展示它們如何 - 使用如此簡單的機制 - 解鎖我們無法想到的潛在應用其他 DL 架構的上下文。
這種簡單性受到許多阻礙其表達能力的問題的限制(至少目前來說),研究人員的目標是克服它,以尋求利用圖數據的全部力量。至于我,我閱讀了不同的論文,討論了一些 GNN 的限制和瓶頸,但將它們統一起來的一個共同點是,所有這些問題都可以與我們用來訓練圖模型的主要機制相關聯,即消息傳遞。
我可能不是專家,但我必須提出一些問題。繼續列舉這些問題并試圖解決它們真的值得嗎?既然我們仍處于這樣一個有趣領域的第一次迭代中,為什么不考慮一種新機制并嘗試一下呢?
作者:Anas AIT AOMAR原文地址:https://towardsdatascience.com/over-smoothing-issue-in-graph-neural-network-bddc8fbc2472
翻譯(轉自):DeepHub IMBA
編輯:jq
-
神經網絡
+關注
關注
42文章
4814瀏覽量
103513
原文標題:圖神經網絡中的過平滑問題
文章出處:【微信號:sessdw,微信公眾號:三星半導體互動平臺】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
神經網絡專家系統在電機故障診斷中的應用
BP神經網絡與卷積神經網絡的比較
什么是BP神經網絡的反向傳播算法
BP神經網絡與深度學習的關系
BP神經網絡的基本原理
BP神經網絡在圖像識別中的應用
人工神經網絡的原理和多種神經網絡架構方法
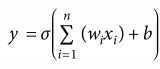





 如何解決圖神經網絡中的過平滑問題
如何解決圖神經網絡中的過平滑問題











評論