分析線性系統的古典方法是微分方程法。描述系統的微分方程中，包含有激勵函數和響應函數以及它們對時間的各階導數的線性組合。線性系統的分析歸結為求解線性微分方程。因為這樣一個分析求解的過程，都是在時域中進行的，所涉及的都是時間變量t，所以這種解微分方程的方法稱為時域分析法。

進行時域分析時，首先是列出系統的微分方程，這個工作并不困難。對于線性電路，只要根據基爾霍夫定理，就可以列出一個或一組電路的線性微分方程。

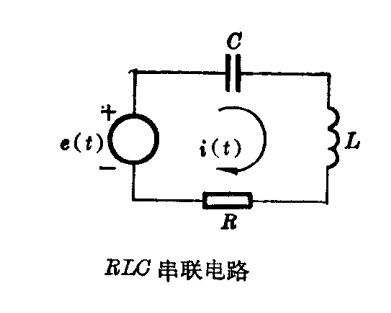
例如，對于RLC串聯電路，如所熟知，可以列出如下方程：

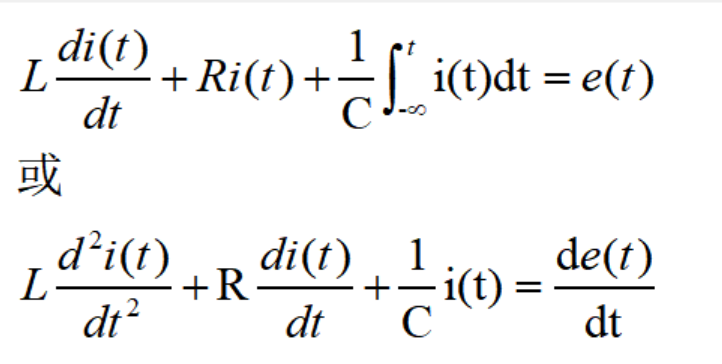
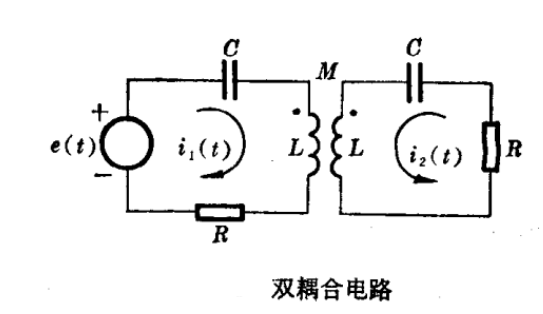
例如，對于圖中所示的雙耦合電路，可以列出一對微分方程：

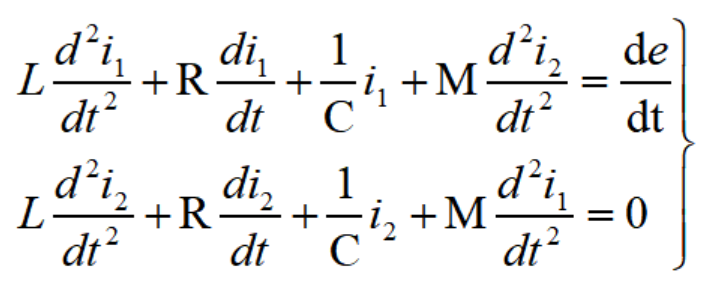
用消元法來求解這兩個聯立的二階微分方程時，就會導得一個四階的微分方程。例如其中消去i1，即可得

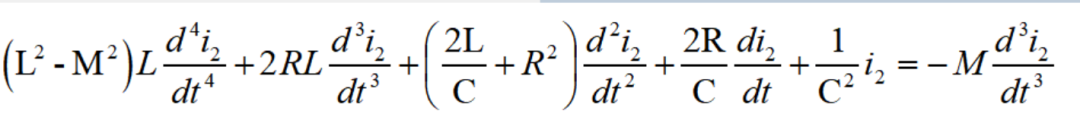
由此推廣到一般，對于一個線性系統，其激勵函數與響應函數、或者輸入函數與輸出函數之間的關系，總可以用下列形式的微分方程式——輸入-輸出方程來描述：

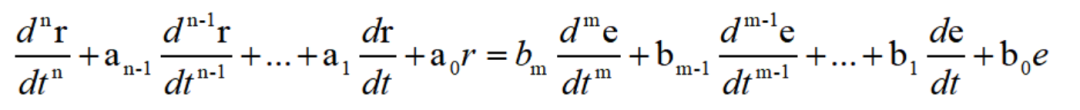
這個式子是一個常系數的n解線性常微分方程，在做線性系統的分析時，就必須要求解這個微分方程。

在高等數學中，這個微分方程式的解包括兩個組成部分：一是此方程相應的齊次方程(令該式右邊為零所得的方程)的通解，另一是滿足此非齊次方程的一個特解。

齊次方程的通解為n個指數項之和，其中包含有n個未定常數，需要用n個初始條件確定。作為系統的響應來說，通解的這部分就是自由響應。

非齊次方程的特解，要根據方程右邊函數即系統的激勵函數的具體形式來求解，作為系統的響應來說，特解的這部分就是受迫響應。

對于一個可以用低階微分方程描述的系統，如果激勵信號又是直流、正弦或者指數之類的簡單形式的函數，那么用上述古典的求解微分方程的方法去分析線性系統是很方便的。但是，如果激勵信號是某種較為復雜的函數時，求方程的特解就不那么容易了。特別是當系統又須用高階微分方程描述時，利用古典法求解微分方程的工作將變得格外困難。

正是避免這種困難，人們找到了利用變換域的方法去求解微分方程并分析系統。在上世紀四、五十年代以前，對于較為復雜的系統的分析，幾乎無一例外地采用拉普拉斯變換法。

然而，應用拉普拉斯變換法以避免古典法遇到的困難，必須付出進行正反兩次變換的代價。這個變換工作，有時并不輕松。特別是在工程技術中，常常會遇到激勵函數是某一個數據的序列或是某一條曲線而無法表示為簡明的解析式的情況，這樣的函數當然也就難以對他進行變換了。這時拉普拉斯變換法也顯得無能為力。

根據電路理論，系統的響應并不一定要劃分為自由響應和受迫響應兩個部分，而可以根據疊加加定理，把它分為僅由初始條件引起的零輸入響應和僅由外加激勵源引起的零狀態響應兩部分。

在求零輸入響應時，只要求解上述齊次方程并利用初始條件確定解中的待定系數，這個工作無大困難。

在求零狀態響應時，就是求解包含激勵函數在內的初始條件為零的非齊次方程。

對于復雜信號激勵的線性系統，在時域中求解系統的非齊次微分方程的解的另一條路子是應用疊加積分。正好像把激勵信號在頻域中分解成單元激勵函數那樣，激勵信號也可以在時域中分解為脈沖信號或階躍信號。

把這些單元激勵分別加于系統并求出其響應，然后把這些響應疊加，即可得到復雜信號加于系統的零狀態響應。基于這種思想所導得的疊加積分，就是卷積積分與杜阿美爾積分，而這兩者之間，具有十分密切的關系。

編輯：jq