作者: 安德魯·卡特(Andrew Carter)
磁場(chǎng)將對(duì)單個(gè)運(yùn)動(dòng)電荷施加力,并且還將對(duì)電流(運(yùn)動(dòng)電荷的集合)施加力。長(zhǎng)度為l的導(dǎo)線在磁場(chǎng)B中承載電流I時(shí)遇到的力用以下公式表示。
[tex] F = ILB sin Theta [/ tex]
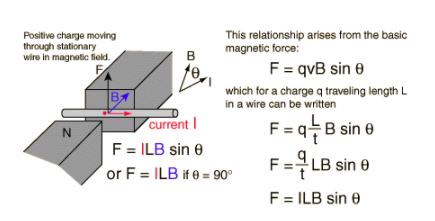
載流導(dǎo)線上的磁力垂直于導(dǎo)線,磁場(chǎng)的位置由右手定則給出。
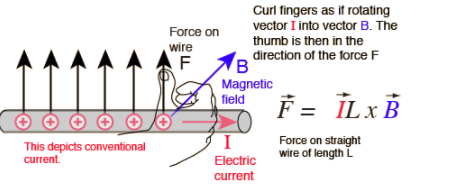
如果電流與磁場(chǎng)之間的夾角為texB [/ tex];[tex] B = 0 [/ tex],然后[tex] sinbeta = 0 [/ tex],[tex] F = 0 [/ tex],[tex] beta = 180 [/ tex],然后[tex] sinbeta = 0 [/ tex],[tex] F = 0 [/ tex],[tex] beta = 90 [/ tex],然后[tex] sinbeta = 1 [/ tex],[tex] F = Bil [/ tex]。因此,如果電流和磁場(chǎng)的方向彼此平行,則不會(huì)在導(dǎo)線上施加力。
作用在帶電粒子上的力
上面解釋了作用在電流上的力。電流是由帶電粒子的運(yùn)動(dòng)產(chǎn)生的。因此,載流線上的力是該電流作用在每個(gè)帶電粒子上的力的總和。如果粒子的電荷為q,速度為v,并且位于具有強(qiáng)度B的力作用在該粒子上的磁場(chǎng)中,則β是速度與磁場(chǎng)之間的夾角,公式為:[tex] = qvBsinbeta [ / tex]。
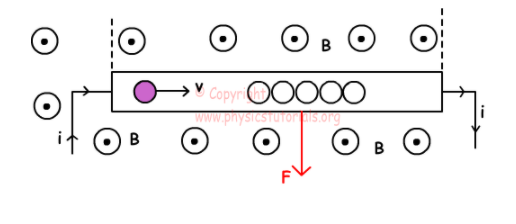
發(fā)生條件:
1.如果tex v =0π/ tex,則tex F =0π/ tex,在磁場(chǎng)中沒有力施加在靜止粒子上。
2.如果∑β = 0 [/ tex],則∑sin0 = 0 [/ tex]和∑F = 0 [/ tex]。
3.如果tex = 180 [/ tex],則ssin180 = 0 [/ tex],且texF = 0 [/ tex],磁場(chǎng)線和粒子的速度彼此平行,那么就沒有力了。
4.如果[β] = 90 [/ tex],則[αsin90= 1] / [tex],[f] F = qvB [/ tex]。v
條件發(fā)生:
1.如果v = 0,則F = 0磁場(chǎng)中沒有力作用在靜止粒子上。
2.如果beta = 0,則sin0 = 0,F(xiàn) = 0
3.如果beta = 180,則sin180 = 0,F(xiàn) = 0,磁場(chǎng)線和粒子的速度彼此平行,則沒有力施加。
4.如果beta = 90,則sin90 = 1,F(xiàn) = qvB
電線上相互承載電流的力
它表明,同一方向上的電流會(huì)相互吸引,因?yàn)樗鼈儠?huì)產(chǎn)生相反的磁場(chǎng)。另一方面,相反方向的電流彼此排斥,因?yàn)樗鼈儺a(chǎn)生具有相同方向的磁場(chǎng)。使用公式,我們可以找到施加在每個(gè)力上的力。
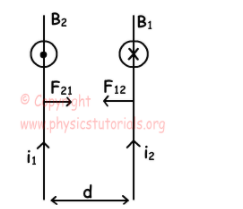
[tex] F = B_1i_2I = 2kfrac {i_1i_2} m5kw60s9xdeh I [/ tex]
其中,tex1 [/ tex]是導(dǎo)線的長(zhǎng)度,tex [dtex // tex]是導(dǎo)線之間的距離。
示例問題:
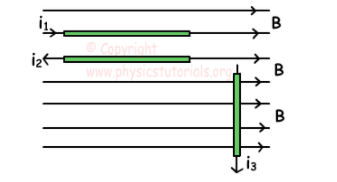
如果將texI_2 [/ tex]放置在恒定磁場(chǎng)中,則求出作用在電流texI_1 [/ tex]上的磁力的方向。
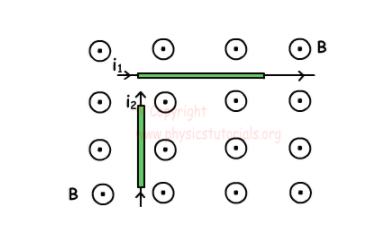
解決方案:
因此,遵循右手定則,答案顯示在下面的i中;
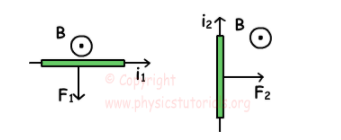
霍爾效應(yīng)
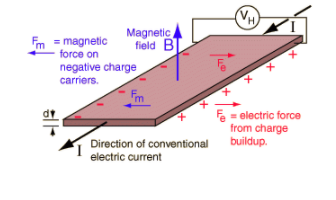
霍爾效應(yīng)是對(duì)電荷移動(dòng)產(chǎn)生的作用力的一種很好的應(yīng)用。這也是測(cè)量磁場(chǎng)強(qiáng)度的常用方法。薄扁平導(dǎo)體兩側(cè)的電荷積聚將平衡這種電磁影響,從而在導(dǎo)體的兩側(cè)之間產(chǎn)生可測(cè)量的電壓。這種可測(cè)量的橫向電壓的存在稱為霍爾效應(yīng)。
霍爾系數(shù)表示為感應(yīng)電場(chǎng)與電流密度和磁場(chǎng)乘積之比。它具有制成導(dǎo)體的材料的特征,其值取決于構(gòu)成電流的電荷載流子的類型,數(shù)量和特性。
編輯:hfy
-
霍爾效應(yīng)
+關(guān)注
關(guān)注
5文章
479瀏覽量
43772
發(fā)布評(píng)論請(qǐng)先 登錄
電感在電路中的作用 電感對(duì)電流的影響分析
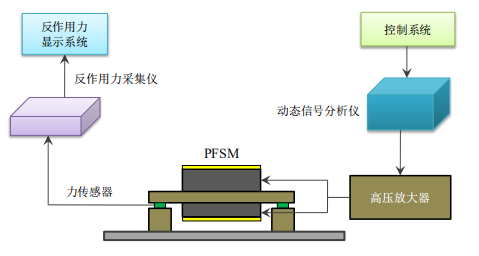
安泰高壓放大器在大口徑壓電傾斜鏡的反作用力研究中的應(yīng)用
磁通門電流傳感器的應(yīng)用及與霍爾電流傳感器的對(duì)比






 磁場(chǎng)中電流的作用力 電線上相互承載電流的力
磁場(chǎng)中電流的作用力 電線上相互承載電流的力










評(píng)論