中學時，提到電阻，會想到阻值和歐姆定律這些等。 提到阻性分析，聯想到伏安曲線分析。

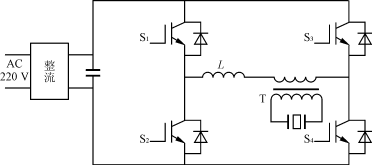
電阻在電路中用途很多很廣。通常設計產品的時候，負載也許在某種環境下，除了本身的原生特性，還可能會產生其他的特性，如阻性、容性和感性。舉例：2020年口罩機的超聲波電源和振子，超聲波電源就是驅動振子，而振子是感性負載，所以在設計超聲波電源的時候，就要考慮到設計的電路和波形是不是會受到這些特性的影響。

阻性分析仿真：（軟件：tina-ti），推導出阻性的數學模型。

1、 正弦波在純阻性分析

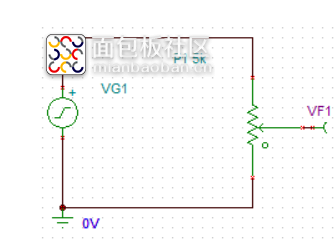
VF2:ui （1V 50HZ ） VF1:uo

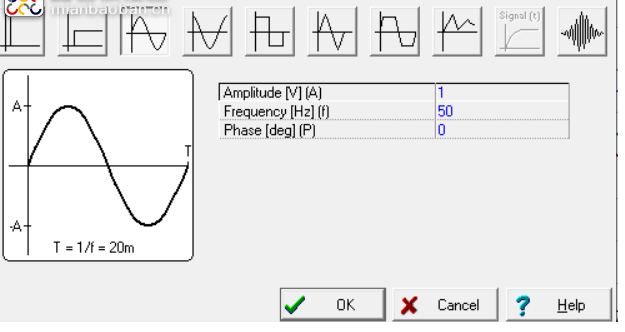
V2（Ui）波形：直流分量為0V，幅度為1V，周期為20ms，以相位由0開始的時域連續周期性函數。

純電阻電阻比值為50%，即2.5k（0.5W）。

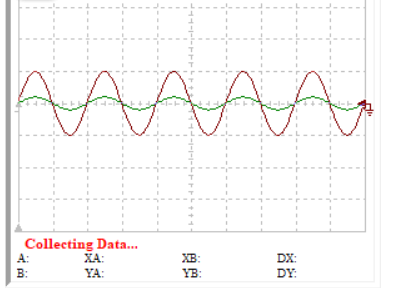
測試波形如下：

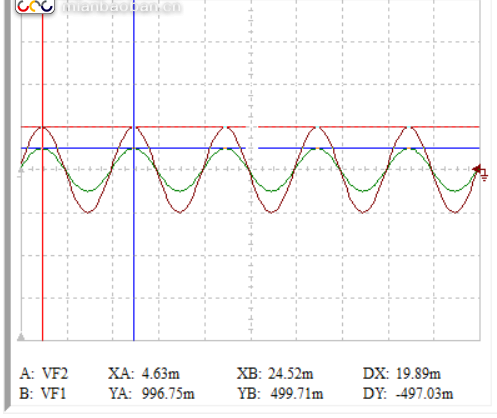
A： VF2:ui VP:1V（996.75m）

B： VF1:uo VP:0.5V（499.71m）

測試結果：純阻性元件不會影響輸入電壓波形的相位和波形主要形狀，但是會影響波形的幅度，但呈現線性關系。是消耗能量（電能）的性質。

純阻性的信號分析完畢。

2、高頻電阻模型

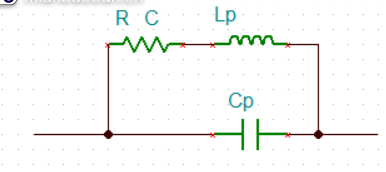
高頻的電阻等效模型

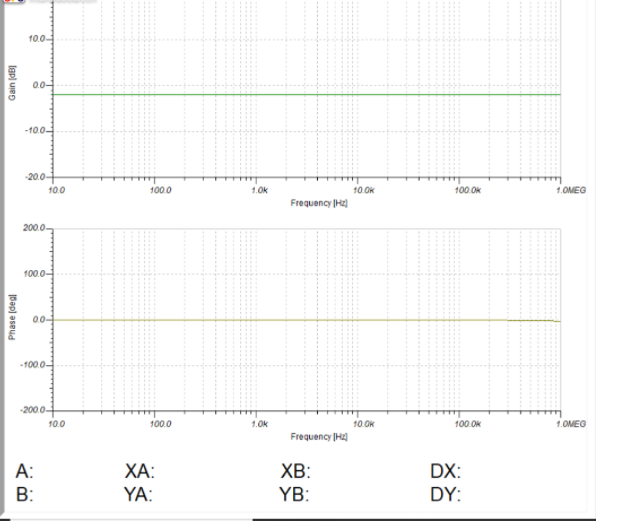
1）50%的阻值比

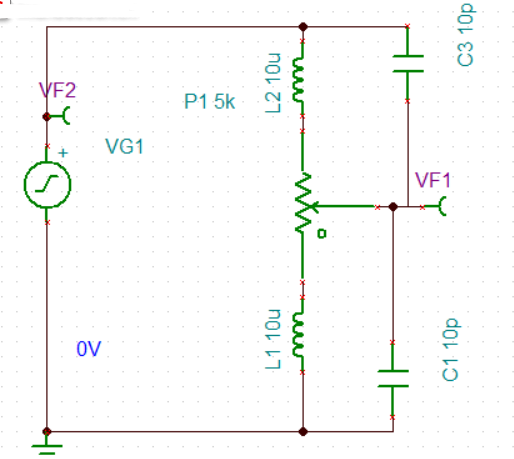
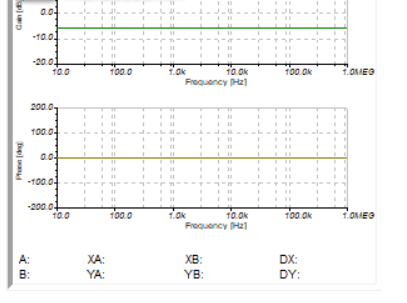
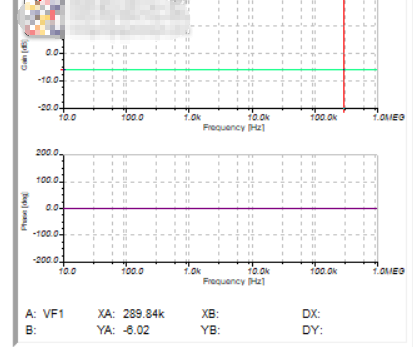
單上下端的電阻值相等和性質一樣的時候，（0-1MHZ）波形都是一個非常完美的狀態和平衡。

1）20%的阻值比

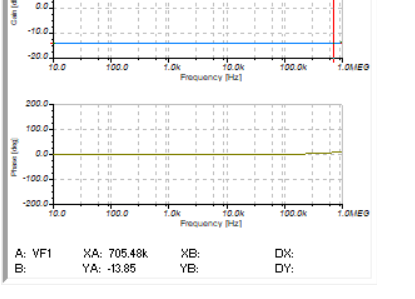
在頻率增加的時候，增益增加了，相位超前了。

3）80%的阻值比

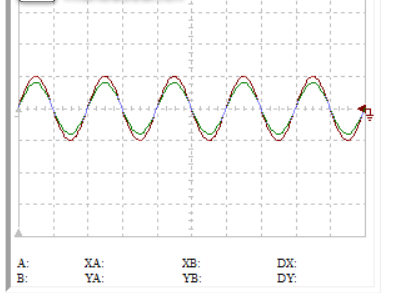
在頻率增加的時候，增益增加了，相位滯后了。

測試小結結論

1） 阻值匹配，使得高頻信號能等時等長，同時到達（不超前不滯后）

2） 運用阻容器件，可以巧妙進行相位補償

3） 高阻抗，對于處理小信號，會對噪聲有抑制作用

4） 時鐘信號和敏感信號線路盡量短，阻值等長

5） 阻性可以吸收波形（如反射）、差分電路阻抗相等等等

這里主要就是推導出阻性在電路的數學模型。

（1） 在相同條件下，1：1的情況下：Uo（t）=p *Ui（t） （P為比例常數，如電阻比值；Ui為輸入波形，t為時間）

（2） 在阻抗不一，和頻率變化的情況下：Uo（t）= （ p + C ） * Ui（t + ph） （P為比例常數，C為不確定增益常量，Ui為輸入波形，ph為不確定相位常量）
編輯：hfy