功率譜估計在分析平穩各態遍歷隨機信號頻率成分領域被廣泛使用,并且已被成功應用到雷達信號處理、故障診斷等實際工程中。本文給出了經典功率譜估計的幾類方法,并通過Matlab的實驗仿真對經典功率譜估計方法性能進行了分析,最后說明了經典功率譜估計法的局限性和造成這種局限性的原因。
1.引言
給定一個標準的正弦信號,我們可以通過傅里葉變換來分析它的頻率成分。然而,實際工程應用中,由于存在著各種干擾、噪聲,我們得到的信號往往不是理想的,如圖1-1這種信號,具有不確定性,幅度不能預知,非周期,但往往服從一定的統計特性,這種信號叫作隨機信號。需要注意的是,本文所說的隨機信號是指平穩各態遍歷的隨機信號,關于非平穩隨機信號的分析方法[1]本文不予討論。

圖1-1 一種隨機信號時域形式
對于圖1-1的隨機信號,我們可以通過功率譜來分析它的頻率成分,如圖1-2所示為圖1-1隨機信號的功率譜。實際過程中,我們只能獲得隨機信號的一些離散數據點(假設為N個),本文將討論如何利用這N個數據點,來得到一個"非精確"的功率譜來對真實隨機信號的功率譜進行估計,并討論如何更好的估計,即在下一章要講述的幾個經典的功率譜估計法。
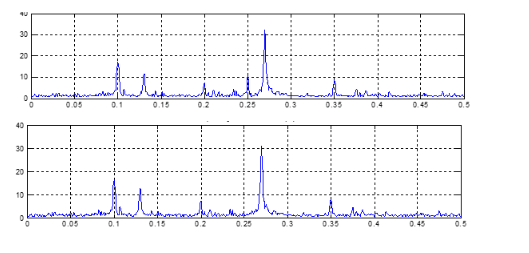
圖1-2 上圖所示的隨機信號功率譜
2.經典功率譜估計法
上一章我們已經知道功率譜估計法是通過利用已經獲得的N個數據點,來得到一個"非精確"的功率譜對真實隨機信號的功率譜進行估計,所以在給出具體的方法之前,如何來評價我們得出的這個"非精確"的功率譜的好壞呢?
評價功率譜性能好壞的標準有很多,本文只給出兩個影響最大的標準:分辨率和方差。分辨率即功率譜上能夠區分的最小相鄰頻率成分,分辨率越高,我們觀察信號的頻率成分越清晰;方差大小則反映到功率譜波動性的大小,如果方差太大,功率譜波動性大,則很容易造成有用的頻率成分被噪聲淹沒。所以,我們希望得到的這個"非精確"的功率譜,分辨率越高越好,方差越小越好。

2.1.2周期圖法性能(Matlab仿真)
上一小節我們已經給出了周期圖法的原理。本節將通過Matlab仿真給出數據點數N對功率譜性能好壞的影響,正如上文所述,將通過對所得功率譜的分辨率和方差兩方面進行分析。
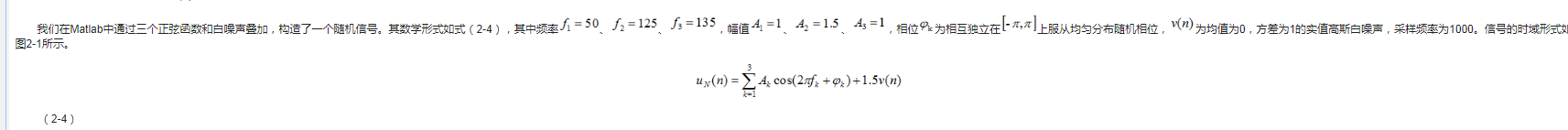

圖2-1 實驗所用的隨機信號
當數據點數N分別為128、256、512和1024時,得到的功率譜分別如圖2-2、圖2-3、圖2-4和圖2-5所示。分辨率能夠直觀的通過功率譜圖形看出,方差的數值由表2-1給出。


表2-1 不同N值得到功率譜的方差值
| N | 128 | 256 | 512 | 1024 |
| 方差 | 92.7108 | 130.9109 | 160.9187 | 483.5894 |
通過上面實驗結果的比較,我們很容易發現,周期圖法得到的功率譜隨著數據點數N的增大,分辨率變大、方差變也大。
2.1.3平均周期圖法
周期圖法得到的功率譜與我們所期望的"分辨率大、方差小"是矛盾的。為了進一步降低方差,將N個觀測樣本數據點分為L段,每段數據長度為M, 分別對每段數據求周期圖功率譜估計,然后求平均值,這種方法稱平均周期圖法。

2.1.4平均周期圖法性能(Matlab仿真)
當數據點數N為1024,分段數分別為8、4、2時,平均周期圖法得到的功率譜分別如圖2-6、圖2-7、圖2-8所示。分辨率能夠直觀的通過功率譜圖形看出,方差的數值由表2-2給出。

表2-2 不同L值得到功率譜的方差值
| L | 8 | 4 | 2 | 1 |
| 方差 | 96.3756 | 190.9647 | 400.6464 | 483.5894 |
L=1時,平均周期圖法退化為周期圖法。通過上面實驗結果的比較,我們很容易發現,平均周期圖法得到的功率譜隨著分段數L變大,方差變小,但分辨率變小。
當觀測樣本序列數據個數N固定時,要降低方差需要增加分段數L。當N不大時分段長度M取值較小,則功率譜分辨率降低到較低的水平。若分段數L固定時,增加分辨率需要分段長度M,則需要采集到更長的檢測數據序列。實際中恰恰是檢測樣本序列長度不足。
2.1.5修正的平均周期圖法
上一節已經提到實際中檢測樣本序列長度是有限的。對現有數據長度N,如果能獲得更多的段數分割,將會得到更小的方差。允許數據段間有重疊部分,來得到更多的段數。對段間重疊長度的選取,最簡單是取為段長度M的一半。由式(2-5)可知更多的段數可以進一步降低方差。
數據截斷的過程中相當于數據加矩形窗,矩形窗幅度較大的旁瓣會造成"頻譜泄漏"。我們分段時采取的窗函數更為多樣(三角窗,海明窗等), 以減小截斷數據(加矩形窗)窗函數帶來的影響[2]
2.1.6修正的平均周期圖法性能(Matlab仿真)
利用修正平均周期圖法,分別使用矩形窗、Blackman窗和Hamming窗得到的功率譜如圖2-9所示。

圖2-9 不同窗函數的修正平均周期圖法得到的功率譜
可以發現,矩形窗的分辨率最高,但是方差也最大,這是由于矩形窗頻譜主瓣最窄,分辨率因此最高,旁瓣也高,導致頻譜泄漏最嚴重,方差最大。
2.1.7總結
周期圖法獲得的功率譜隨著樣本點數越多,分辨率越大、方差越大;平均周期圖法以犧牲分辨率來進一步改善方差;修正的平均周期圖法允許段的重疊來進一步增大分段數、或者分段數相同,每段樣本點數變多。無論是哪種方法都沒有徹底結局方差與分辨率之間的矛盾。
2.2相關功率譜估計法-BT法
正如我們之前介紹的,要提高功率譜估計的分辨率,必須增加數據序列的長度N,但是較長的數據序列,由噪聲引起的隨機性得到更為充分的體現-較大的方差。事實上,當N無窮大時,方差為一非零常數。即周期圖法無法實現功率譜的一致估計。而這節講述的相關功率譜估計法(下文稱作BT法),是一致估計。
2.2.1 BT法的原理
維納辛欽定理指出,隨機信號的相關函數與它的功率譜是一對傅里葉變換對。BT法就是基于這個原理。先由觀測數據估計出自相關函數,然后求自相關函數的傅立葉變換,以此變換作為對功率譜的估計,也稱為間接法。BT法要求信號長度N以外的信號為零,這也造成BT法的局限性。
2.2.2 BT法的性能(Matlab仿真)
數據點數N分別為128、256、512和1024的BT法,得到的功率譜如圖2-10、圖2-11、圖2-12和圖2-13所示。


圖2-13 N=1024時,BT法得到的功率譜
由上面實驗可以發現,M隨著N的增大而增大時,分辨率提高,方差變大。BT法仍然沒有解決分辨率與方差之間的矛盾,但是BT法得到的功率譜當N為無窮大時,方差會趨向于零,即為一致估計[2]。
2.2.3 周期圖法與BT法的關系

結 論
本文通過Matlab仿真,以一個具體的隨機信號為例,簡單介紹了周期圖法、平均周期圖法、修正的平均周期圖法以及BT法的基本原理,并對這些方法的性能進行分析。可以看出,無論是周期圖法及其改進算法還是BT法都沒有從根本上解決分辨率與方差的矛盾。經典功率譜估計是利用傅里葉變換估計功率譜,而我們之前分析隨機信號不滿足傅里葉變換的條件,所以經典功率譜估計方法不得不從無限長數據點截取有限長數據點,加入限制條件(周期圖法實際上假定N點外數據周期重復、BT法假定N點外數據為零)來"強制"作傅里葉變換,這也是造成它局限性的原因。
參考資料
[1]朱哲,鐘宏偉. 非平穩隨機信號分析處理方法研究[J] 安徽電子信息技術學院學報2008.6:28-28
[2]皇甫堪.現代數字信號處理[M].電子工業出版社
-
功率譜
+關注
關注
0文章
13瀏覽量
8446 -
雷達信號處理
+關注
關注
2文章
13瀏覽量
9378
發布評論請先 登錄
怎么利用matlab得到95%,80%和70%的置信區間,并生成不同區間下的功率誤差貝塔分布?
進群免費領FPGA學習資料!數字信號處理、傅里葉變換與FPGA開發等
MATLAB仿真在直流電機雙閉環調速系統中的應用
用matlab里的simulink仿真一個推挽升壓仿真電路,輸出帶載能力很差?
這些電源常用仿真軟件,你都知道嗎?
Matlab/Simulink/Stateflow建模開發及仿真測試
PPEC-HIL 三相整流逆變實時仿真測試
寬帶功率放大器在可調諧激光器解調實驗的應用






 基于Matlab實驗仿真對經典功率譜估計性能分析
基于Matlab實驗仿真對經典功率譜估計性能分析













評論