為何從零開始?
有許多深度學習庫(Keras、TensorFlow和PyTorch等)可僅用幾行代碼構建一個神經(jīng)網(wǎng)絡。然而,如果你真想了解神經(jīng)網(wǎng)絡的底層運作,建議學習如何使用Python或任何其他編程語言從零開始為神經(jīng)網(wǎng)絡編程。
不妨創(chuàng)建某個隨機數(shù)據(jù)集:
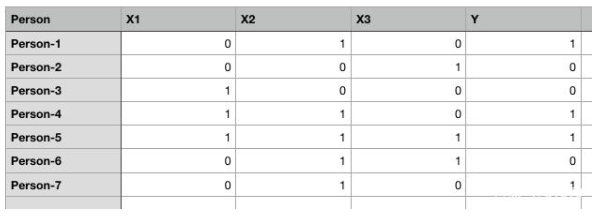
圖1. 為簡單起見,隨機數(shù)據(jù)集帶二進制值
上面表格有五列:Person、X1、X2、X3和Y。1表示true,0表示false。我們的任務是創(chuàng)建一個能夠基于X1、X2和X3的值來預測Y值的人工神經(jīng)網(wǎng)絡。
我們將創(chuàng)建一個有1個輸入層、1個輸出層而沒有隱藏層的人工神經(jīng)網(wǎng)絡。開始編程前,先不妨看看我們的神經(jīng)網(wǎng)絡在理論上將如何執(zhí)行:
ANN理論
人工神經(jīng)網(wǎng)絡是一種監(jiān)督式學習算法,這意味著我們?yōu)樗峁┖凶宰兞康妮斎霐?shù)據(jù)和含有因變量的輸出數(shù)據(jù)。比如在該示例中,自變量是X1、X2和X3,因變量是Y。
首先,ANN進行一些隨機預測,將這些預測與正確的輸出進行比較,計算出誤差(預測值與實際值之間的差)。找出實際值與傳播值之間的差異的函數(shù)名為成本函數(shù)(cost function)。這里的成本指誤差。我們的目標是使成本函數(shù)最小化。訓練神經(jīng)網(wǎng)絡基本上是指使成本函數(shù)最小化。下面會介紹如何執(zhí)行此任務。
神經(jīng)網(wǎng)絡分兩個階段執(zhí)行:前饋階段和反向傳播階段。下面詳細介紹這兩個步驟。
前饋
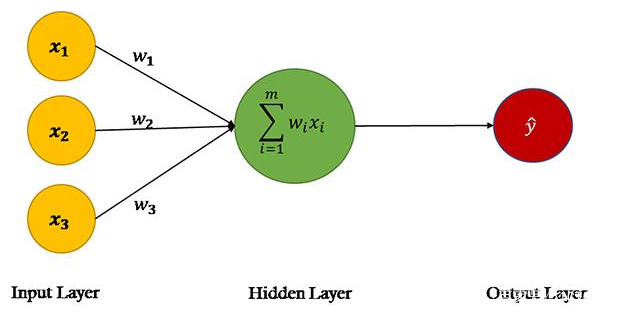
圖2
來源:單層神經(jīng)網(wǎng)絡,又叫Perceptron
在ANN的前饋階段,基于輸入節(jié)點中的值和權重進行預測。如果看一下上圖中的神經(jīng)網(wǎng)絡,會看到數(shù)據(jù)集中有三個特征:X1、X2和X3,因此第一層(又叫輸入層)中有三個節(jié)點。
神經(jīng)網(wǎng)絡的權重基本上是我們要調(diào)整的字符串,以便能夠正確預測輸出。請記住,每個輸入特性只有一個權重。
以下是在ANN的前饋階段所執(zhí)行的步驟:
第1步:計算輸入和權重之間的點積
輸入層中的節(jié)點通過三個權重參數(shù)與輸出層連接。在輸出層中,輸入節(jié)點中的值與對應的權重相乘并相加。最后,偏置項b添加到總和。
為什么需要偏置項?
假設某個人有輸入值(0,0,0),輸入節(jié)點和權重的乘積之和將為零。在這種情況下,無論我們怎么訓練算法,輸出都將始終為零。因此,為了能夠做出預測,即使我們沒有關于該人的任何非零信息,也需要一個偏置項。偏置項對于構建穩(wěn)健的神經(jīng)網(wǎng)絡而言必不可少。
數(shù)學上,點積的總和:
X.W=x1.w1 + x2.w2 + x3.w3 + b
第2步:通過激活函數(shù)傳遞點積(X.W)的總和
點積XW可以生成任何一組值。然而在我們的輸出中,我們有1和0形式的值。我們希望輸出有同樣的格式。為此,我們需要一個激活函數(shù)(Activation Function),它將輸入值限制在0到1之間。因此,我們當然會使用Sigmoid激活函數(shù)。
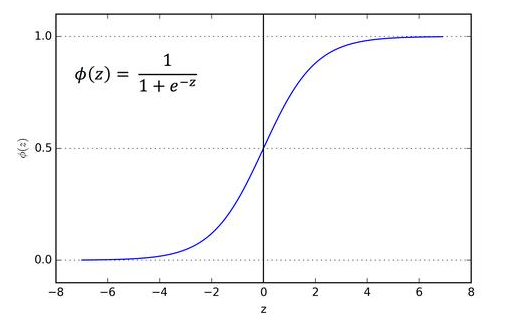
圖3. Sigmoid激活函數(shù)
輸入為0時,Sigmoid函數(shù)返回0.5。如果輸入是大正數(shù),返回接近1的值。負輸入的情況下,Sigmoid函數(shù)輸出的值接近零。
因此,它特別適用于我們要預測概率作為輸出的模型。由于概念只存在于0到1之間,Sigmoid函數(shù)是適合我們這個問題的選擇。
上圖中z是點積X.W的總和。
數(shù)學上,Sigmoid激活函數(shù)是:
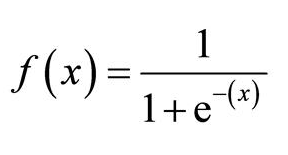
圖4. Sigmoid激活函數(shù)
總結一下到目前為止所做的工作。首先,我們要找到帶權重的輸入特征(自變量矩陣)的點積。接著,通過激活函數(shù)傳遞點積的總和。激活函數(shù)的結果基本上是輸入特征的預測輸出。
反向傳播
一開始,進行任何訓練之前,神經(jīng)網(wǎng)絡進行隨機預測,這種預測當然是不正確的。
我們先讓網(wǎng)絡做出隨機輸出預測。然后,我們將神經(jīng)網(wǎng)絡的預測輸出與實際輸出進行比較。接下來,我們更新權重和偏置,并確保預測輸出更接近實際輸出。在這個階段,我們訓練算法。不妨看一下反向傳播階段涉及的步驟。
第1步:計算成本
此階段的第一步是找到預測成本。可以通過找到預測輸出值和實際輸出值之間的差來計算預測成本。如果差很大,成本也將很大。
我們將使用均方誤差即MSE成本函數(shù)。成本函數(shù)是找到給定輸出預測成本的函數(shù)。
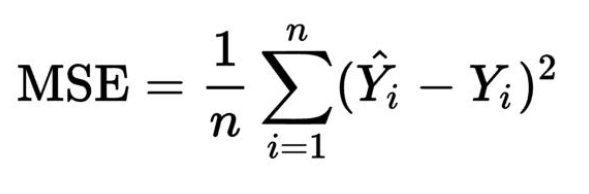
圖5. 均方誤差
這里,Yi是實際輸出值,i是預測輸出值,n是觀察次數(shù)。
第2步:使成本最小化
我們的最終目的是微調(diào)神經(jīng)網(wǎng)絡的權重,并使成本最小化。如果你觀察仔細,會了解到我們只能控制權重和偏置,其他一切不在控制范圍之內(nèi)。我們無法控制輸入,無法控制點積,無法操縱Sigmoid函數(shù)。
為了使成本最小化,我們需要找到權重和偏置值,確保成本函數(shù)返回最小值。成本越小,預測就越正確。
要找到函數(shù)的最小值,我們可以使用梯度下降算法。梯度下降可以用數(shù)學表示為:

圖6. 使用梯度下降更新權重
Error是成本函數(shù)。上面的等式告訴我們找到關于每個權重和偏置的成本函數(shù)的偏導數(shù),然后從現(xiàn)有權重中減去結果以得到新的權重。
函數(shù)的導數(shù)給出了在任何給定點的斜率。為了找到成本是增加還是減少,給定權重值,我們可以找到該特定權重值的函數(shù)導數(shù)。如果成本隨重量增加而增加,導數(shù)將返回正值,然后將其從現(xiàn)有值中減去。
另一方面,如果成本隨重量增加而降低,將返回負值,該值將被添加到現(xiàn)有的權重值中,因為負負得正。
在上面公式中,a名為學習速率,乘以導數(shù)。學習速率決定了我們的算法學習的速度。
我們需要對所有權重和偏置重復執(zhí)行梯度下降操作,直到成本最小化,并且成本函數(shù)返回的值接近零。
現(xiàn)在是實現(xiàn)我們迄今為止研究的人工神經(jīng)網(wǎng)絡的時候了。我們將用Python創(chuàng)建一個簡單的神經(jīng)網(wǎng)絡,有1個輸入層和1個輸出層。
使用numpy實現(xiàn)人工神經(jīng)網(wǎng)絡
圖7
圖片來源:hackernoon.com
要采取的步驟:
1.定義自變量和因變量
2.定義超參數(shù)
3.定義激活函數(shù)及其導數(shù)
4.訓練模型
5.做出預測
第1步:先創(chuàng)建自變量或輸入特征集以及相應的因變量或標簽。
#Independent variables
input_set = np.array([[0,1,0],
[0,0,1],
[1,0,0],
[1,1,0],
[1,1,1],
[0,1,1],
[0,1,0]])#Dependent variable
labels = np.array([[1,
0,
0,
1,
1,
0,
1]])
labels = labels.reshape(7,1) #toconvert labels to vector
我們的輸入集含有七個記錄。同樣,我們還創(chuàng)建了一個標簽集,含有輸入集中每個記錄的對應標簽。標簽是我們希望ANN預測的值。
第2步:定義超參數(shù)。
我們將使用numpy的random.seed函數(shù),以便在執(zhí)行以下代碼時可以獲得同樣的隨機值。
接下來,我們使用正態(tài)分布的隨機數(shù)初始化權重。由于輸入中有三個特征,因此我們有三個權重的向量。然后,我們使用另一個隨機數(shù)初始化偏置值。最后,我們將學習速率設置為0.05。
np.random.seed(42)
weights = np.random.rand(3,1)
bias = np.random.rand(1)
lr = 0.05 #learning rate
第3步:定義激活函數(shù)及其導數(shù):我們的激活函數(shù)是Sigmoid函數(shù)。
def sigmoid(x):
return 1/(1+np.exp(-x))
現(xiàn)在定義計算Sigmoid函數(shù)導數(shù)的函數(shù)。
def sigmoid_derivative(x):
return sigmoid(x)*(1-sigmoid(x))
第4步:是時候訓練ANN模型了。
我們將從定義輪次(epoch)數(shù)量開始。輪次是我們想針對數(shù)據(jù)集訓練算法的次數(shù)。我們將針對數(shù)據(jù)訓練算法25000次,因此epoch將為25000。可以嘗試不同的數(shù)字以進一步降低成本。
for epoch in range(25000):
inputs = input_set
XW = np.dot(inputs, weights)+ bias
z = sigmoid(XW)
error = z - labels
print(error.sum())
dcost = error
dpred = sigmoid_derivative(z)
z_del = dcost * dpred
inputs = input_set.T
weights = weights - lr*np.dot(inputs, z_del)
for num in z_del:
bias = bias - lr*num
不妨了解每個步驟,然后進入到預測的最后一步。
我們將輸入input_set中的值存儲到input變量中,以便在每次迭代中都保留input_set的值不變。
inputs = input_set
接下來,我們找到輸入和權重的點積,并為其添加偏置。(前饋階段的第1步)
XW = np.dot(inputs, weights)+ bias
接下來,我們通過Sigmoid激活函數(shù)傳遞點積。(前饋階段的第2步)
z = sigmoid(XW)
這就完成了算法的前饋部分,現(xiàn)在是開始反向傳播的時候了。
變量z含有預測的輸出。反向傳播的第一步是找到誤差。
error = z - labels
print(error.sum())
我們知道成本函數(shù)是:
圖8
我們需要從每個權重方面求該函數(shù)的微分,這可以使用微分鏈式法則(chain rule of differentiation)來輕松完成。我將跳過推導部分,但如果有人感興趣,請留言。
因此,就任何權重而言,成本函數(shù)的最終導數(shù)是:
slope = input x dcost x dpred
現(xiàn)在,斜率可以簡化為:
dcost = error
dpred = sigmoid_derivative(z)
z_del = dcost * dpred
inputs = input_set.T
weights = weight-lr*np.dot(inputs, z_del)
我們有z_del變量,含有dcost和dpred的乘積。我們拿輸入特征矩陣的轉(zhuǎn)置與z_del相乘,而不是遍歷每個記錄并拿輸入與對應的z_del相乘。
最后,我們將學習速率變量lr與導數(shù)相乘,以加快學習速度。
除了更新權重外,我們還要更新偏置項。
for num in z_del:
bias = bias - lr*num
一旦循環(huán)開始,你會看到總誤差開始減小;訓練結束時,誤差將保留為很小的值。
-0.001415035616137969
-0.0014150128584959256
-0.0014149901015685952
-0.0014149673453557714
-0.0014149445898578358
-0.00141492183507419
-0.0014148990810050437
-0.0014148763276499686
-0.0014148535750089977
-0.0014148308230825385
-0.0014148080718707524
-0.0014147853213728624
-0.0014147625715897338
-0.0014147398225201734
-0.0014147170741648386
-0.001414694326523502
-0.001414671579597255
-0.0014146488333842064
-0.0014146260878853782
-0.0014146033431002465
-0.001414580599029179
-0.0014145578556723406
-0.0014145351130293877
-0.0014145123710998
-0.0014144896298846701
-0.0014144668893831067
-0.001414444149595611
-0.0014144214105213174
-0.0014143986721605849
-0.0014143759345140276
-0.0014143531975805163
-0.001414330461361444
-0.0014143077258557749
-0.0014142849910631708
-0.00141426225698401
-0.0014142395236186895
-0.0014142167909661323
-0.001414194059027955
-0.001414171327803089
-0.001414148597290995
-0.0014141258674925626
-0.0014141031384067547
-0.0014140804100348098
-0.0014140576823759854
-0.0014140349554301636
-0.0014140122291978665
-0.001413989503678362
-0.001413966778871751
-0.001413944054778446
-0.0014139213313983257
-0.0014138986087308195
-0.0014138758867765552
-0.0014138531655347973
-0.001413830445006264
-0.0014138077251906606
-0.001413785006087985
-0.0014137622876977014
-0.0014137395700206355
-0.0014137168530558228
-0.0014136941368045382
-0.0014136714212651114
-0.0014136487064390219
-0.0014136259923249635
-0.001413603278923519
-0.0014135805662344007
-0.0014135578542581566
-0.0014135351429944293
-0.0014135124324428719
-0.0014134897226037203
-0.0014134670134771238
-0.0014134443050626295
-0.0014134215973605428
-0.0014133988903706311
第5步:作出預測
是時候作出一些預測了。先用[1,0,0]試一下:
single_pt = np.array([1,0,0])
result = sigmoid(np.dot(single_pt, weights) + bias)
print(result)
輸出:
[0.01031463]
如你所見,輸出更接近0而不是1,因此分類為0。
不妨再用[0,1,0]試一下:
single_pt = np.array([0,1,0])
result = sigmoid(np.dot(single_pt, weights) + bias)
print(result)
輸出:
[0.99440207]
如你所見,輸出更接近1而不是0,因此分類為1。
結論
我們在本文中學習了如何使用numpy Python庫,從零開始創(chuàng)建一個很簡單的人工神經(jīng)網(wǎng)絡,只有1個輸入層和1個輸出層。該ANN能夠?qū)€性可分離數(shù)據(jù)進行分類。
如果我們有非線性可分離的數(shù)據(jù),我們的ANN就無法對這種類型的數(shù)據(jù)進行分類。下篇將介紹如何構建這樣的ANN。
-
神經(jīng)網(wǎng)絡
+關注
關注
42文章
4814瀏覽量
103519 -
編程語言
+關注
關注
10文章
1956瀏覽量
36610 -
深度學習
+關注
關注
73文章
5560瀏覽量
122769
發(fā)布評論請先 登錄
無刷電機小波神經(jīng)網(wǎng)絡轉(zhuǎn)子位置檢測方法的研究
低功耗+AI識別:基于樹莓派的 LoRa 神經(jīng)網(wǎng)絡安防系統(tǒng)!

基于FPGA搭建神經(jīng)網(wǎng)絡的步驟解析
BP神經(jīng)網(wǎng)絡與卷積神經(jīng)網(wǎng)絡的比較
BP神經(jīng)網(wǎng)絡的優(yōu)缺點分析
深度學習入門:簡單神經(jīng)網(wǎng)絡的構建與實現(xiàn)
人工神經(jīng)網(wǎng)絡的原理和多種神經(jīng)網(wǎng)絡架構方法
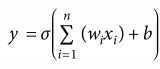
卷積神經(jīng)網(wǎng)絡與傳統(tǒng)神經(jīng)網(wǎng)絡的比較
RNN模型與傳統(tǒng)神經(jīng)網(wǎng)絡的區(qū)別
如何使用Python構建LSTM神經(jīng)網(wǎng)絡模型
Moku人工神經(jīng)網(wǎng)絡101






 使用numpy Python庫從零開始構建人工神經(jīng)網(wǎng)絡
使用numpy Python庫從零開始構建人工神經(jīng)網(wǎng)絡











評論