概述

線性回歸是利用數理統計中回歸分析，來確定兩種或兩種以上變量間相互依賴的定量關系的一種統計分析方法，運用十分廣泛。其表達形式為y = w’x+e，e為誤差服從均值為0的正態分布。

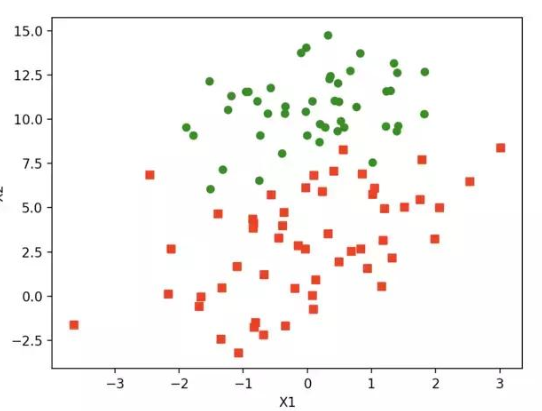
回歸分析中，只包括一個自變量和一個因變量，且二者的關系可用一條直線近似表示，這種回歸分析稱為一元線性回歸分析。如果回歸分析中包括兩個或兩個以上的自變量，且因變量和自變量之間是線性關系，則稱為多元線性回歸分析。

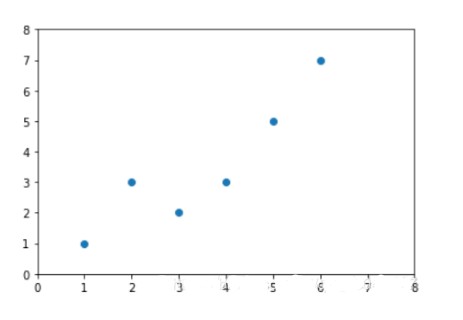
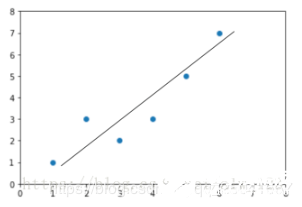
通過線性回歸構造出來的函數一般稱之為了線性回歸模型。線性回歸模型的函數一般寫作為：

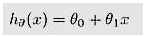
損失函數

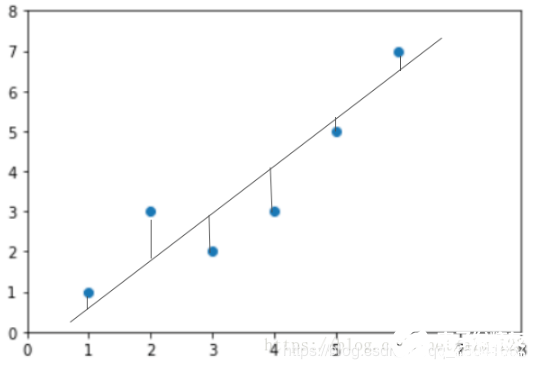
把每條小豎線的長度加起來就是預測值與真實值的差距。那每條小豎線的長度的加和怎么算？其實就是歐式距離加和，公式如下：

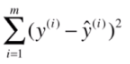
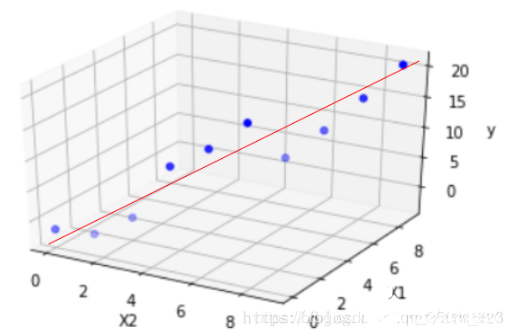
通過線性回歸算法，我們可能會得到很多的線性回歸模型，但是不同的模型對于數據的擬合或者是描述能力是不一樣的。我們的目的最終是需要找到一個能夠最精確地描述數據之間關系的線性回歸模型。這是就需要用到代價函數。代價函數就是用來描述線性回歸模型與正式數據之前的差異。如果完全沒有差異，則說明此線性回歸模型完全描述數據之前的關系。如果需要找到最佳擬合的線性回歸模型，就需要使得對應的代價函數最小，相關的公式描述如下：

Hypothesis：表示的就是線性回歸模型

Cost Function：代價函數

Goal：就是要求對應的代價函數最小

線性回歸模型求解

假設在線性回歸模型中僅僅只存在一個函數，就是斜率參數。即theta-0是0。如果存在如下的數據：

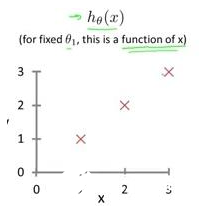
圖中對應的3個點分別為（1，1），（2，2），（3，3）那么很明顯，最佳線性回歸模型就是h（x）=x。如果通過實驗證明呢？我們畫出在theta-1處于不同值的代價函數。

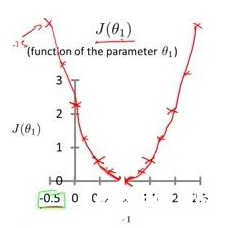
線性回歸模型的特點

① 建模速度快，不需要很復雜的計算，在數據量大的情況下依然運行速度很快。

② 可以根據系數給出每個變量的理解和解釋。

③ 對異常值很敏感。