補碼乘法,補碼乘法計算詳細解說
1.補碼與真值得轉換公式
補碼乘法因符號位參與運算，可以完成補碼數的“直接”乘法，而不需要求補級。這種直接的方法排除了較慢的對2求補操作，因而大大加速了乘法過程。
首先說明與直接的補碼乘法相聯系數學特征。對于計算補碼數的數值來說，一種較好的表示方法是使補碼的位置數由一個帶負權的符號和帶正權的系數。今考慮一個定點補碼整數[N]補＝anan－1…a1a0，這里an是符號位。根據[N]補的符號，補碼數[N]補和真值N的關系可以表示成：
如果我們把負權因數－2n強加到符號位an上，那么就可以把上述方程組中的兩個位置表達式合并成下面的統一形式：
??? 
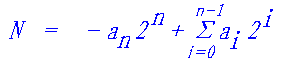??? (2.29)
[例19] 已知: [N1]補 ＝ (01101)2，[N2]補＝(10011)2，求[N1]補，[N2]補具有的數值。
[解:]
[N1]補＝(01101)2 具有的數值為：
N1＝－0×24＋1×23＋1×22＋0×21＋1×20＝(＋13)10
[N2]補＝(10011)2 具有的數值為：
N2＝－1×24＋0×23＋0×22＋1×21＋1×20＝(－13)10
?2.一般化的全加器形式
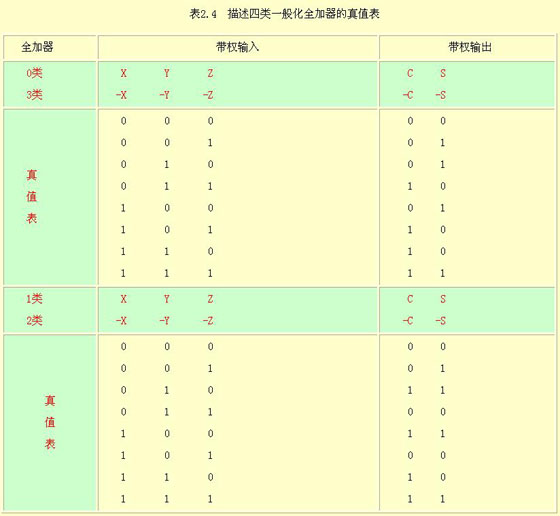
常規的一位全加器可假定它的3個輸入和2個輸出都是正權。這種加法器通過把正權或負權加到輸入/輸出端，可以歸納出四類加法單元。如右表，0類全加器沒有負權輸入；1類全加器有1個負權輸入和2個正權輸入；依次類推。
對0類、3類全加器而言有：
??? S＝XYZ＋XYZ＋XYZ＋XYZ
??? C＝XY＋YZ＋ZX
對1類、2類全加器，則有
??? S＝XYZ＋XYZ＋XYZ＋XYZ
??? C＝XY＋XZ＋YZ
表2.3 四類一般化全加器的名稱和邏輯符號
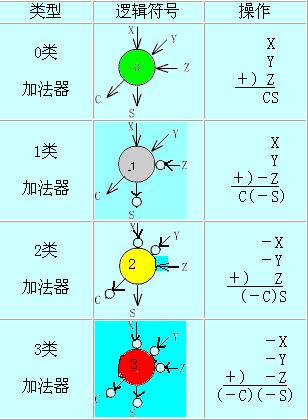
注意，0類和3類全加器是用同一對邏輯方程來表征的，它和普通的一位全加器(0類)是一致的。這是因為3類全加器可以簡單地把0類全加器的所有輸入輸出值全部反向來得到，反之亦然。1類和2類全加器之間也能建立類似的關系。由于邏輯表達式具有兩級與一或形式，可以用“與或非”門來實現，延遲時間為2T。
3.直接補碼陣列乘法器
利用混合型的全加器就可以構成直接補碼數陣列乘法器。設被乘數A和乘數B是兩個5位的二進制補碼數，即
A＝(a4)a3a2a1a0
B＝(b4)a3a2a1a0
它們具有帶負權的符號位a4和b4，并用括號標注。如果我們用括號來標注負的被加項，例如(aibj)，那么A和B相乘過程中所包含的操作步驟如下面矩陣所示：
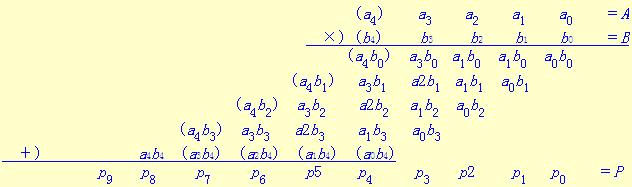
5位乘5位的直接補碼陣列乘法器邏輯原理。
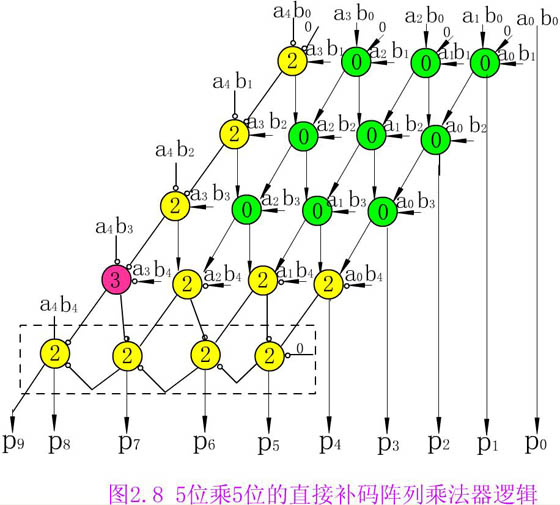
其中使用不同的邏輯符號來代表0類、1類、2類、3類全加器。2類和1類全加器具有同樣的結構，但是使用不同的邏輯符號可使乘法陣列的線路圖容易理解。
在n位乘n位的一般情況下，該乘法器需要(n－2)2個0類全加器，(n－2)個1類全加器，(2n－3)個2類全加器，1個3類全加器，總共是n(n－1)個全加器。 故所需的總乘法時間是：
tp=Ta+2(n-1)Tf=2T+(2n-2)2T=(4n-2)T (2.31)
[例20] 設[A]補＝(01101)2，[B]補＝(11011)2，求[A×B]補＝?
[解:]
驗證：
－1×27＋0×26＋1×25＋1×24＋1×23＋1×22＋1×21＋1×20
＝－128＋(32＋16＋8＋4＋2＋1)
＝－65
(13)×(－5)＝－65
非常好我支持^.^
(453) 40.4%
不好我反對
(667) 59.6%
相關閱讀：
( 發表人：admin )