1.可控加法/減法(CAS)單元
　　
　　和陣列乘法器非常相似，陣列式除法器也是一種并行運算部件，采用大規(guī)模集成電路制造。與早期的串行除法器相比，陣列除法器不僅所需的控制線路少，而且能提供令人滿意的高速運算速度。
　　
　　陣列除法器有多種多樣形式，如不恢復(fù)余數(shù)陣列除法器，補碼陣列除法器等等。
　　
　　首先介紹可控加法/減法(CAS)單元，它將用于并行除法流水邏輯陣列中，它有四個輸出端和四個輸入端。當(dāng)輸入線P＝0時，CAS作加法運算；當(dāng)P＝1時，CAS作減法運算。邏輯結(jié)構(gòu)圖：

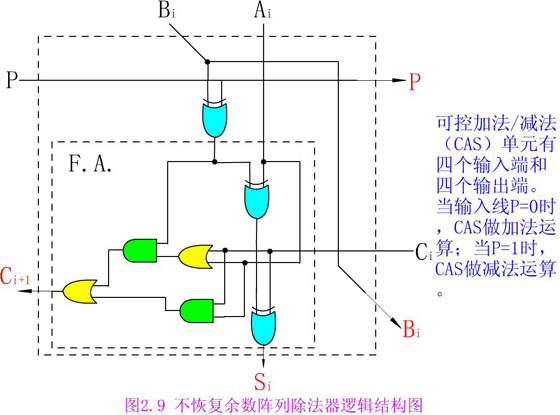
CAS單元的輸入與輸出的關(guān)系可用如下一組邏輯方程來表示：
　　
　　S_i＝A_i⊕(B_i⊕P)⊕C_i
　　C_i＋1＝(A_i＋C_i)·(B_i⊕P)＋A_iC_i????? (2.32)
　　
　　當(dāng)P＝0時，方程式(2.32)就等于式(2.23)，即得我們熟悉的一位全加器(FA)的公式：
　　
　　Si＝Ai⊕Bi⊕Ci
　　Ci＋1＝AiBi＋BiCi＋AiCi
　　
　　當(dāng)P＝1時，則得求差公式：
　　
　　S_i＝A_i⊕B_i⊕C_i
　　C_i＋1＝A_iB_i＋B_iC_i＋A_iC_i???????????? (2.33)
　　
　　其中B_i＝B_i⊕1。
　　
　　在減法情況下，輸入C_i稱為借位輸入，而C_i＋1稱為借位輸出。
　　
　　為說明CAS單元的實際內(nèi)部電路實現(xiàn)，將方程式(2.32)加以變換，可得如下形式：
　　
　　S_i＝A_i⊕(B_i⊕P)⊕C_i
　　＝A_iB_iC_iP＋A_iB_iC_iP＋A_iB_iC_iP＋A_iB_iC_iP＋A_iB_iC_iP＋A_iB_iC_iP＋A_iB_iC_iP＋A_iB_iC_iP
　　
　　C_i＋1＝(A_i＋C_i)(B_i⊕P)＋A_iC_i
　　＝A_iB_iP＋A_iB_iP＋B_iC_iP＋B_iC_iP＋A_iC_i
　　
　　在這兩個表達式中，每一個都能用一個三級組合邏輯電路(包括反向器)來實現(xiàn)。因此每一個基本的CAS單元的延遲時間為3T單元。

?2.不恢復(fù)余數(shù)的陣列除法器
　　
　　假定所有被處理的數(shù)都是正的小數(shù)。
　　
　　不恢復(fù)余數(shù)的除法也就是加減交替法。在不恢復(fù)余數(shù)的除法陣列中，每一行所執(zhí)行的操作究竟是加法還是減法，取決于前一行輸出的符號與被除數(shù)的符號是否一致。當(dāng)出現(xiàn)不夠減時，部分余數(shù)相對于被除數(shù)來說要改變符號。這時應(yīng)該產(chǎn)生一個商位“0”，除數(shù)首先沿對角線右移，然后加到下一行的部分余數(shù)上。當(dāng)部分余數(shù)不改變它的符號時，即產(chǎn)生商位“1”，下一行的操作應(yīng)該是減法。下圖示出了4位除4位的不恢復(fù)余數(shù)陣列除法器的邏輯原理圖。其中
　　
　　被除數(shù)　x＝0.ｘ₁ｘ₂ｘ₃ｘ₄ｘ₅ｘ₆ (雙倍長)
　　除數(shù)　　y＝0.ｙ₁ｙ₂ｙ₃
　　商數(shù)　　q＝0.q₁q₂q₃
　　余數(shù)　　r＝0.00r₃r₄r₅r₆
　　字長　　n＋1＝4

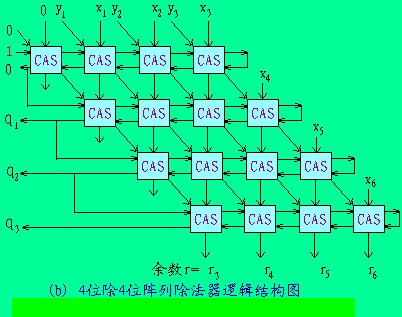
圖2.9　不恢復(fù)余數(shù)陣列除法器邏輯結(jié)構(gòu)圖

　　由圖看出，該陣列除法器是用一個可控加法/減法(CAS)單元所組成的流水陣列來實現(xiàn)的。推廣到一般情況，一個(n＋1)位除(n＋1)位的加減交替除法陣列由(n＋1)2個CAS單元組成，其中兩個操作數(shù)(被除數(shù)與除數(shù))都是正的。

單元之間的互連是用n＝3的陣列來表示的。這里被除數(shù)ｘ是一個6位的小數(shù)(雙倍長度值)：
　　
　　ｘ＝0.ｘ₁ｘ₂ｘ₃ｘ₄ｘ₅ｘ₆
　　
　　它是由頂部一行和最右邊的對角線上的垂直輸入線來提供的。
　　
　　除數(shù)ｙ是一個3位的小數(shù)：
　　
　　ｙ＝0.ｙ₁ｙ₂ｙ₃
　　
　　它沿對角線方向進入這個陣列。這是因為，在除法中所需要的部分余數(shù)的左移，可以用下列等效的操作來代替：即讓余數(shù)保持固定，而將除數(shù)沿對角線右移。
　　
　　商q是一個3位的小數(shù)：
　　
　　q＝0.q₁q₂q₃
　　
　　它在陣列的左邊產(chǎn)生。
　　
　　余數(shù)r是一個6位的小數(shù)：
　　
　　r＝0.00r₃r₄r₅r₆
　　
　　它在陣列的最下一行產(chǎn)生。
　　
　　最上面一行所執(zhí)行的初始操作經(jīng)常是減法。因此最上面一行的控制線P固定置成“1”。減法是用2的補碼運算來實現(xiàn)的，這時右端各CAS單元上的反饋線用作初始的進位輸入。每一行最左邊的單元的進位輸出決定著商的數(shù)值。將當(dāng)前的商反饋到下一行，我們就能確定下一行的操作。由于進位輸出信號指示出當(dāng)前的部分余數(shù)的符號，因此，它將決定下一行的操作將進行加法還是減法。
　　
　　對不恢復(fù)余數(shù)陣列除法器來說，在進行運算時，沿著每一行都有進位(或借位)傳播，同時所有行在它們的進位鏈上都是串行連接。而每個CAS單元的延遲時間為3T單元，因此，對一個2n位除以n位的不恢復(fù)余數(shù)陣列除法器來說，單元的數(shù)量為(n＋1)2，考慮最大情況下的信號延遲，其除法執(zhí)行時間為
　　
　　td＝3(n＋1)²T　　　　　　　　　　　　　　(2.34)
　　
　　其中n為尾數(shù)位數(shù)。

[例20] ｘ＝0.101001， ｙ＝0.111， 求q =ｘ÷ｙ。
　　
　　[解:]
　　
　　[x]_補＝0.101001
　　
　　[y]_補＝0.111? [－ｙ]_補＝1.001

　　故得

　　商 q＝q₀.q₁q₂q₃＝0.101
　　余數(shù) r＝(0.00r₃r₄r₅r₆)＝0.000110

　　我們看到，當(dāng)被除數(shù)ｘ和除數(shù)ｙ送至陣列除法器輸入端后，經(jīng)過3(n＋1)T時間延遲，便在除法器輸出端得到穩(wěn)定的商數(shù)q和余數(shù)r的信號電平。與串行除法器相比，明顯的優(yōu)點是省去了復(fù)雜的控制線路，提高了運算速度。