上文講述毫米波通信優勢的文章中提到了香農定理和香農極限,本著再學習的態度,我們詳細整理一下關于香農的一切。
?
Claude Elwood Shannon
(1916年4月30日—2001年2月24日)
克勞德·艾爾伍德·香農(Claude Elwood Shannon ,1916年4月30日—2001年2月24日)是美國數學家、信息論的創始人。1936年獲得密歇根大學學士學位[1]?。1940年在麻省理工學院獲得碩士和博士學位,1941年進入貝爾實驗室工作。香農提出了信息熵的概念,為信息論和數字通信奠定了基礎。主要論文有:1938年的碩士論文《繼電器與開關電路的符號分析》,1948年的《通訊的數學原理》和1949年的《噪聲下的通信》。
人物資料
克勞德·艾爾伍德·香農(Claude Elwood Shannon,1916-2001)1916年4月30日誕生于美國密西根州的Petoskey。在Gaylord小鎮長大,當時鎮里只有三千居民。父親是該鎮的法官,他們父子的姓名完全相同,都是Claude Elwood Shannon。母親是鎮里的中學校長,姓名是Mabel Wolf Shannon。他生長在一個有良好教育的環境,不過父母給他的科學影響好像還不如祖父的影響大。香農的祖父是一位農場主兼發明家,發明過洗衣機和許多農業機械,這對香農的影響比較直接。此外,香農的家庭與大發明家愛迪生(Thomas Alva Edison,1847-1931)還有遠親關系。香農的大部分時間是在貝爾實驗室和MIT(麻省理工學院)度過的。在“功成名就”后,香農與瑪麗(Mary Elizabeth Moore)1949年3月27日結婚,他們是在貝爾實驗室相識的,瑪麗當時是數據分析員。他們共有四個孩子:三個兒子羅伯特(Robert)、詹姆斯(James)、安德魯莫瑞(Andrew Moore)和一個女兒Margarita Catherine。后來身邊還有兩個可愛的孫女。
2001年2月24日,香農在馬薩諸塞州Medford辭世,享年84歲。貝爾實驗室和MIT發表的訃告都尊崇香農為信息論及數字通信時代的奠基人。
人物生平
香農于1916年4月30日出生于美國密歇根州的Petoskey,并且是愛迪生的遠親戚。1936年畢業于密歇根大學并獲得數學和電子工程學士學位。1940年獲得麻省理工學院(MIT)數學博士學位和電子工程碩士學位。1941年他加入貝爾實驗室數學部,工作到1972年。1956年他成為麻省理工學院(MIT)客座教授,并于1958年成為終生教授,1978年成為名譽教授。香農博士于2001年2月24日去世,享年84歲。
香農于1940年在普林斯頓高級研究所(The Institute for Advanced Study at Princeton)期間開始思考信息論與有效通信系統的問題。經過8年的努力,香農在1948年6月和10月在《貝爾系統技術雜志》(Bell System Technical Journal)上連載發表了具有深遠影響的論文《通訊的數學原理》。1949年,香農又在該雜志上發表了另一著名論文《噪聲下的通信》。在這兩篇論文中,香農闡明了通信的基本問題,給出了通信系統的模型,提出了信息量的數學表達式,并解決了信道容量、信源統計特性、信源編碼、信道編碼等一系列基本技術問題。兩篇論文成為了信息論的奠基性著作。
1936年香農在密西根大學獲得數學與電氣工程學士學位,然后進入MIT念研究生。
1938年香農在MIT獲得電氣工程碩士學位,碩士論文題目是《A Symbolic Analysis of Relay and Switching Circuits》(繼電器與開關電路的符號分析)。當時他已經注意到電話交換電路與布爾代數之間的類似性,即把布爾代數的“真”與“假”和電路系統的“開”與“關”對應起來,并用1和0表示。于是他用布爾代數分析并優化開關電路,這就奠定了數字電路的理論基礎。哈佛大學的Howard Gardner教授說,“這可能是本世紀最重要、最著名的一篇碩士論文。”
1940年香農在MIT獲得數學博士學位,而他的博士論文卻是關于人類遺傳學的,題目是《An Algebra for Theoretical Genetics》(理論遺傳學的代數學)。這說明香農的科學興趣十分廣泛,后來他在不同的學科方面發表過許多有影響的文章。
在讀學位的同時,他還用部分時間跟溫尼法·布什(Vannevar Bush)教授進行微分分析器的研究。這種分析器是早期的機械模擬計算機,用于獲得常微分方程的數值解。1941年香農發表了《Mathematical theory of the differential analyzer》(微分分析器的數學理論),他寫道:“大多數結果通過證明的定理形式給出。最重要的是處理了一些條件,有些條件可以生成一個或多個變量的函數,有些條件可使常微分方程得到解。還給出了一些注意事項,給出求函數的近似值(不能產生精確值)、求調整率的近似值以及自動控制速率的方法。”
1941年香農以數學研究員的身份進入新澤西州的AT&T貝爾電話公司,并在貝爾實驗室工作到1972年,從24歲到55歲,整整31年。1956年他當了MIT的訪問教授,1958年成為正式教授,1978年退休。
人們描述香農的生活,白天他總是關起門來工作,晚上則騎著他的獨輪車來到貝爾實驗室。他的同事D. Slepian寫到:“我們大家都帶著午飯來上班,飯后在黑板上玩玩數學游戲,但克勞德很少過來。他總是關起門來工作。但是,如果你要找他,他會非常耐心地幫助你。他能立刻抓住問題的本質。他真是一位天才,在我認識的人中,我只對他一人使用這個詞。”
香農與John Riordan一起工作,1942年發表了一篇關于串并聯網絡的雙終端數的論文。這篇論文擴展了麥克馬洪(Percy A. MacMahon,1854-1929)1892年在Electrician上發表的論文理論。
1948年,劃時代的“通信的一個數學理論”分成兩部分,在7月和10月的Bell System Technical Journal發表。文章系統論述了信息的定義,怎樣數量化信息,怎樣更好地對信息進行編碼。在這些研究中,概率理論是香農使用的重要工具。香農同時提出了信息熵的概念,用于衡量消息的不確定性。
在漫長的歲月,他思考過許多問題。除在普林斯頓高等研究院工作過一年外,主要都在MIT和Bell Lab度過。需要說明的是,在二次世界大戰時,香農博士也是一位著名的密碼破譯者(這使人聯想到比他大4歲的圖靈博士)。他在Bell Lab的破譯團隊主要是追蹤德國飛機和火箭,尤其是在德國火箭對英國進行閃電戰時起了很大作用。1949年香農發表了另外一篇重要論文《Communication Theory of Secrecy Systems》(保密系統的通信理論),正是基于這種工作實踐,它的意義是使保密通信由藝術變成科學。
1948年香農在Bell System Technical Journal上發表了《A Mathematical Theory of Communication 》(通訊的數學原理)。論文由香農和威沃共同署名。前輩威沃(Warren Weaver,1894-1978)當時是洛克菲勒基金會自然科學部的主任,他為文章寫了序言。后來,香農仍然從事技術工作,而威沃則研究信息論的哲學問題。順便提一句,該論文剛發表時,使用的是不定冠詞A,收入論文集時改為定冠詞The。

成就與榮譽
香農理論的重要特征是熵(entropy)的概念,他證明熵與信息內容的不確定程度有等價關系。熵曾經是波爾茲曼在熱力學第二定律引入的概念,我們可以把它理解為分子運動的混亂度。香農將統計物理中熵的概念,引申到信道通信的過程中,從而開創了”信息論“這門學科。香農定義的“熵”又被稱為“香農熵” 或 “信息熵”, 即其中i標記概率空間中所有可能的樣本,表示該樣本的出現幾率,K是和單位選取相關的任意常數。可以明顯看出“信息熵”的定義和“熱力學熵”(玻爾茲曼公式)的定義只相差某個比例常數。
熵(entropy)指的是體系的混亂的程度,它在控制論、概率論、數論、天體物理、生命科學等領域都有重要應用,在不同的學科中也有引申出的更為具體的定義,是各領域十分重要的參量。熵由魯道夫·克勞修斯(Rudolf Clausius)提出,并應用在熱力學中。后來在,克勞德·艾爾伍德·香農(Claude Elwood Shannon)第一次將熵的概念引入到信息論中來。
眾所周知,質量、能量和信息量是三個非常重要的量。
人們很早就知道用秤或者天平計量物質的質量,而熱量和功的關系則是到了19世紀中葉,隨著熱功當量的明確和能量守恒定律的建立才逐漸清楚。能量一詞就是它們的總稱,而能量的計量則通過“卡、焦耳”等新單位的出現而得到解決。
然而,關于文字、數字、圖畫、聲音的知識已有幾千年歷史了。但是它們的總稱是什么,它們如何統一地計量,直到19世紀末還沒有被正確地提出來,更談不上如何去解決了。20世紀初期,隨著電報、電話、照片、電視、無線電、雷達等的發展,如何計量信號中信息量的問題被隱約地提上日程。
1928年哈特利(R.V. H. Harley)考慮到從D個彼此不同的符號中取出N個符號并且組成一個“詞”的問題。如果各個符號出現的概率相同,而且是完全隨機選取的,就可以得到D^N個不同的詞。從這些詞里取了特定的一個就對應一個信息量I。哈特利建議用N log D這個量表示信息量,即I=N log D。這里的log表示以10為底的對數。后來,1949年控制論的創始人維納也研究了度量信息的問題,還把它引向熱力學第二定律。
但是就信息傳輸給出基本數學模型的核心人物還是香農。1948年香農長達數十頁的論文“通信的數學理論”成了信息論正式誕生的里程碑。在他的通信數學模型中,清楚地提出信息的度量問題,他把哈特利的公式擴大到概率pi不同的情況,得到了著名的計算信息熵H的公式:

如果計算中的對數log是以2為底的,那么計算出來的信息熵就以比特(bit)為單位。在計算機和通信中廣泛使用的字節(Byte)、KB、MB、GB等詞都是從比特演化而來。“比特”的出現標志著人類知道了如何計量信息量。香農的信息論為明確什么是信息量概念作出決定性的貢獻。
香農在進行信息的定量計算的時候,明確地把信息量定義為隨機不定性程度的減少。這就表明了他對信息的理解:信息是用來減少隨機不定性的東西。或香農逆定義:信息是確定性的增加。
雖然香農的信息概念比以往的認識有了巨大的進步,但仍存在局限性,這一概念同樣沒有包含信息的內容和價值,只考慮了隨機型的不定性,沒有從根本上回答"信息是什么"的問題。
事實上,香農最初的動機是把電話中的噪音除掉,他給出通信速率的上限,這個結論首先用在電話上,后來用到光纖,截止2013又用在無線通信上。我們能夠清晰地打越洋電話或衛星電話,都與通信信道質量的改善密切相關。
克勞德·香農在公眾中并不特別知名,但他是使我們的世界能進行即時通信的少數科學家和思想家之一。他是美國科學院院士、美國工程院院士、英國皇家學會會員、美國哲學學會會員。他獲得過許多榮譽和獎勵。例如1949年Morris獎、1955年Ballantine獎、1962年Kelly獎、1966年的國家科學獎章、IEEE的榮譽獎章、1978年Jaquard獎、1983年Fritz獎、1985年基礎科學京都獎。他接受的榮譽學位不勝枚舉,不再贅述。
我們懷念香農,要熟悉他的兩大貢獻:一是信息理論、信息熵的概念;另一是符號邏輯和開關理論。我們更應該學習他好奇心強、重視實踐、永不滿足的科學精神,這是他獲得成功的重要經驗。
榮譽
美國Alfred Noble協會美國工程師獎 1940年
Morris Liebmann 無線電工程師協會Memorial獎章 1949年
耶魯大學 (首席科學家) 1954年
Stuart Ballantine弗蘭克林協會獎章 1955年
研究合作獎 1956年
密歇根大學,榮譽博士 1961年
萊斯大學 榮譽獎章 1962年
普林斯頓大學 榮譽博士 1962年
Marvin J. Kelly Award 1962年
愛丁堡大學 榮譽博士 1964年
匹茲堡大學 榮譽博士 1964年
電子電氣工程師協會 榮譽獎章 1966年
美國國家科學獎章 1966年 由前總統Lyndon B. 約翰遜頒發
Golden Plate Award 1967年
美國西北大學 榮譽博士 1970年
Harvey Prize,the Technion of Haifa 以色列 1972年
牛津大學 榮譽博士 1978年
Joseph Jacquard獎 1978年
Harold Pender獎 1978年
東英格倫大學 榮譽博士 1982年
卡內基梅隆大學 榮譽博士 1984年
美國聲頻技術協會 金獎 1985年
Kyoto Prize 1985年
塔夫斯大學 榮譽博士 1987年
賓西法尼亞大學 榮譽博士 1991年
Eduard Rhein Prize 1991年
?
香農定理
?
香農定理給出了信道信息傳送速率的上限(比特每秒)和信道信噪比及帶寬的關系。香農定理可以解釋現代各種無線制式由于帶寬不同,所支持的單載波最大吞吐量的不同。
在有隨機熱噪聲的信道上傳輸數據信號時,信道容量Rmax與信道帶寬W,信噪比S/N關系為:Rmax=W*log2(1+S/N)。注意這里的log2是以2為底的對數。

簡介
類比:城市道路上的汽車的車速(業務速率)和什么有關系?
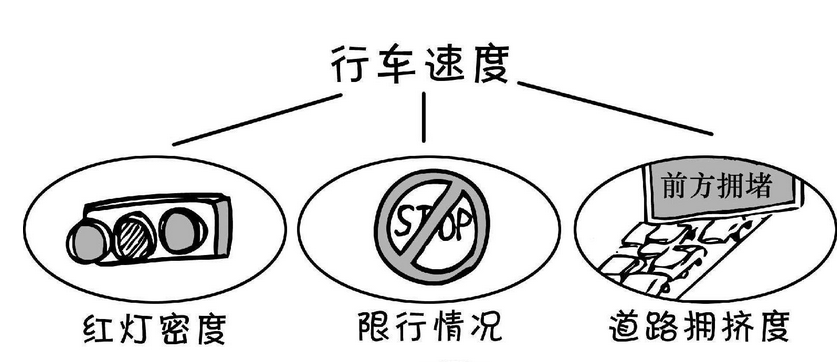
除了和自己車的動力有關之外,主要還受限于道路的寬度(帶寬)和車輛多少、紅燈疏密等其他干擾因素(信噪比),如圖1所示。
?
俗話說:“有線的資源是無限的,而無線的資源卻是有限的。”無線信道并不是可以任意增加傳送信息的速率,它受其固有規律的制約,就像城市道路上的車一樣不能想開多快就開多快,還受到道路寬度、其他車輛數量等因素影響。這個規律就是香農定理。
香農定理是所有通信制式最基本的原理,它描述了有限帶寬、有隨機熱噪聲信道的最大傳輸速率與信道帶寬、信號噪聲功率比之間的關系。其用公式可表示為:
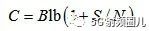
其中:C是信道支持的最大速度或者叫信道容量;B是信道的帶寬;S是平均信號功率;N是平均噪聲功率;S/N即信噪比。
香農定理給出了信道信息傳送速率的上限(比特每秒)和信道信噪比及帶寬的關系。香農定理可以解釋現代各種無線制式由于帶寬不同,所支持的單載波最大吞吐量的不同。
理解香農公式須注意以下幾點:
(1)信道容量由帶寬及信噪比決定,增大帶寬、提高信噪比可以增大信道容量;
(2)在要求的信道容量一定的情況下,提高信噪比可以降低帶寬的需求,增加帶寬可以降低信噪比的需求;
(3)香農公式給出了信道容量的極限,也就是說,實際無線制式中單信道容量不可能超過該極限,只能盡量接近該極限。在卷積編碼條件下,實際信道容量離香農極限還差3dB;在Turbo編碼的條件下,接近了香農極限。
(4)LTE中多天線技術沒有突破香農公式,而是相當于多個單信道的組合。
香農定理可以變換一下形式成為
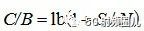
這個C/B就是單位帶寬的容量(業務速率),就是頻譜利用率的概念,也就是說香農定理給出了一定信噪比下頻率利用率的極限。
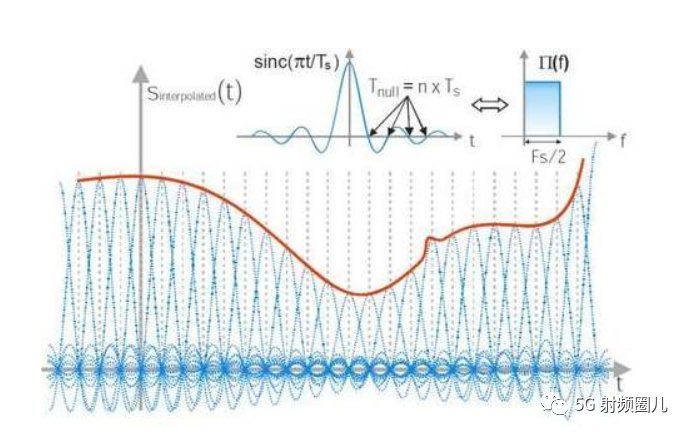
在有隨機熱噪聲的信道上傳輸數據信號時,數據傳輸率Rmax與信道帶寬W,信噪比S/N關系為:Rmax=W*log2(1+S/N)。注意這里的log2是以2為底的對數,下同。
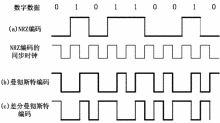
在信號處理和信息理論的相關領域中,通過研究信號在經過一段距離后如何衰減以及一個給定信號能加載多少數據后得到了一個著名的公式,叫做香農(Shannon)定理。它以比特每秒(bps)的形式給出一個鏈路速度的上限,表示為鏈路信噪比的一個函數,鏈路信噪比用分貝(dB)衡量。因此我們可以用香農定理來檢測電話線的數據速率。
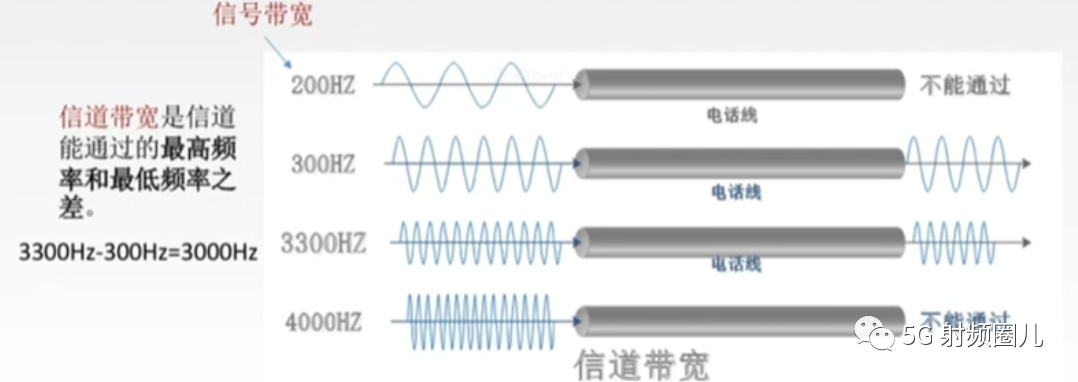
香農定理由如下的公式給出: C=W*log2*(1+S/N) 其中C是可得到的鏈路速度,W是鏈路的帶寬,S是平均信號功率,N是平均噪聲功率,信噪比(S/N)通常用分貝(dB)表示,分貝數=10×log10(S/N)。
通常音頻電話連接支持的頻率范圍為300Hz到3300Hz,則B=3300Hz-300Hz=3000Hz,而一般鏈路典型的信噪比是30dB,即S/N=1000,因此我們有C=3000×log2(1+ 1000),近似等于30Kbps,是28.8Kbps調制解調器的極限,因此如果電話網絡的信噪比沒有改善或不使用壓縮方法,調制解調器將達不到更高的速率。
應用
香農定理用來求信道的最大傳輸速率,即信道容量,當通過信道的信號速率超過香農定理的信道容量時,誤碼率顯著提高,信息質量嚴重下降。需要指出的是這里的信道容量只是理論上可以達到的極限,實際如何達到,該定理不能說明。
? ? ? ?

香農采樣定理
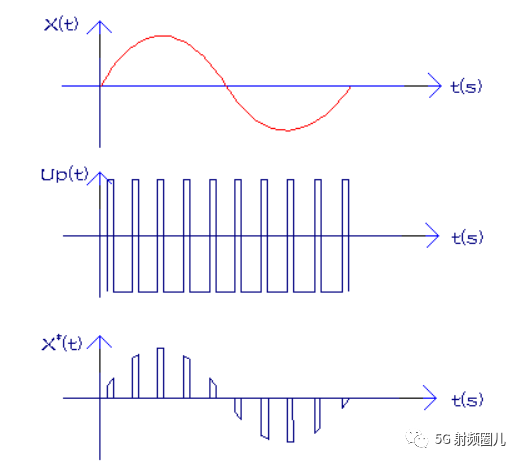
香農采樣定理,又稱奈奎斯特采樣定理,是信息論,特別是通訊與信號處理學科中的一個重要基本結論。1924年奈奎斯特(Nyquist)就推導出在理想低通信道的最高大碼元傳輸速率的公式:理想低通信道的最高大碼元傳輸速率B=2W,信息傳輸
定義
為了不失真地恢復模擬信號,采樣頻率應該不小于模擬信號頻譜中最高頻率的2倍。 f s≥2f max
概念
采樣定理,又稱香農采樣定律、奈奎斯特采樣定律,是信息論,特別是通訊與信號處理學科中的一個重要基本結論.E. T. Whittaker(1915年發表的統計理論),克勞德·香農 與Harry Nyquist都對它作出了重要貢獻。另外,V. A. Kotelnikov 也對這個定理做了重要貢獻。
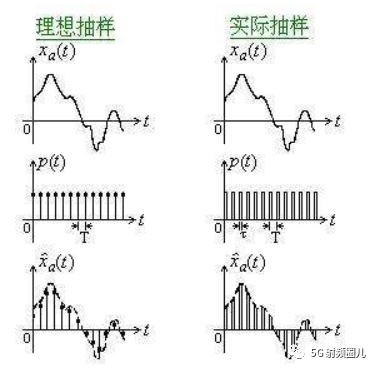
采樣是將一個信號(即時間或空間上的連續函數)轉換成一個數值序列(即時間或空間上的離散函數)。
采樣得到的離散信號經保持器后,得到的是階梯信號,即具有零階保持器的特性。
如果信號是帶限的,并且采樣頻率高于信號最高頻率的一倍,那么,原來的連續信號可以從采樣樣本中完全重建出來。
帶限信號變換的快慢受到它的最高頻率分量的限制,也就是說它的離散時刻采樣表現信號細節的能力是非常有限的。采樣定理是指,如果信號帶寬小于奈奎斯特頻率(即采樣頻率的二分之一),那么此時這些離散的采樣點能夠完全表示原信號。高于或處于奈奎斯特頻率的頻率分量會導致混疊現象。大多數應用都要求避免混疊,混疊問題的嚴重程度與這些混疊頻率分量的相對強度有關。
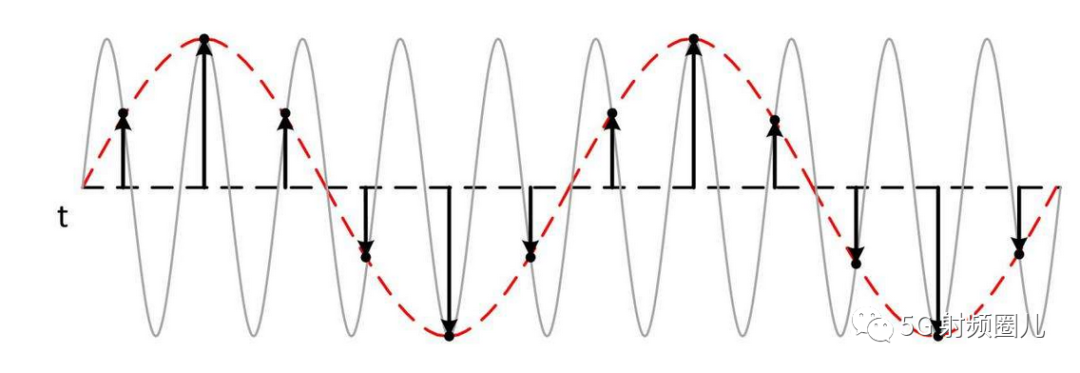
采樣過程所應遵循的規律,又稱取樣定理、抽樣定理。采樣定理說明采樣頻率與信號頻譜之間的關系,是連續信號離散化的基本依據。采樣定理是1928年由美國電信工程師H.奈奎斯特首先提出來的,因此稱為奈奎斯特采樣定理。1933年由蘇聯工程師科捷利尼科夫首次用公式嚴格地表述這一定理,因此在蘇聯文獻中稱為科捷利尼科夫采樣定理。1948年信息論的創始人C.E.香農對這一定理加以明確地說明并正式作為定理引用,因此在許多文獻中又稱為香農采樣定理。采樣定理有許多表述形式,但最基本的表述方式是時域采樣定理和頻域采樣定理。采樣定理在數字式遙測系統、時分制遙測系統、信息處理、數字通信和采樣控制理論等領域得到廣泛的應用。
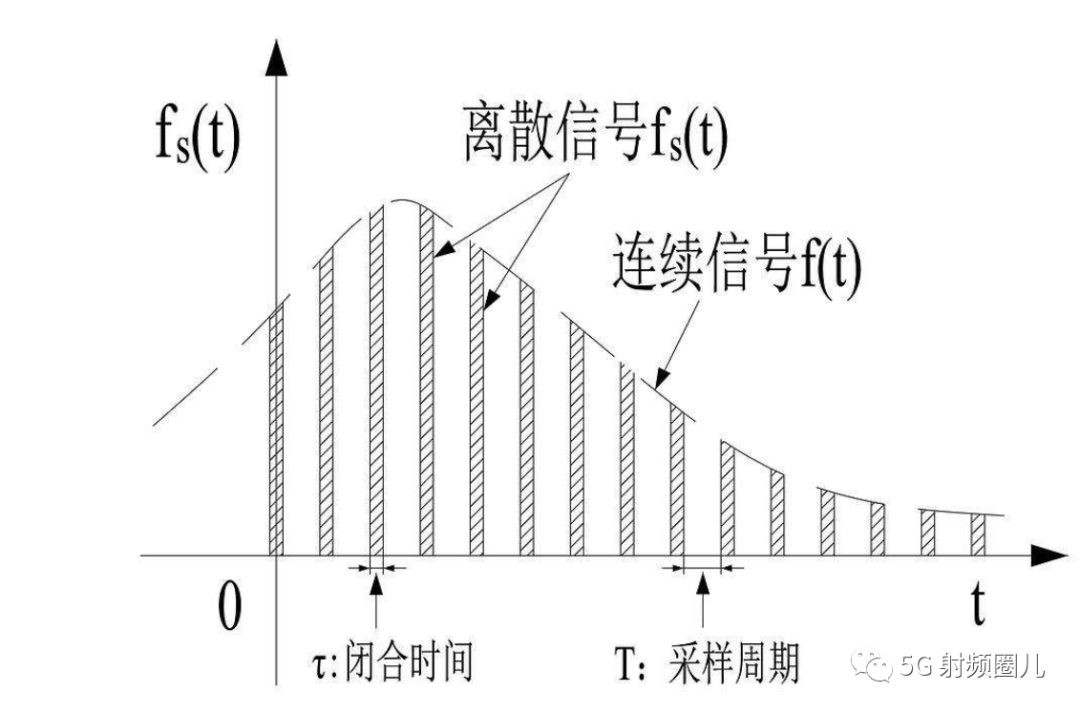
時域采樣定理
頻帶為F的連續信號f(t)可用一系列離散的采樣值f(t1),f(t1±Δt),f(t1±2Δt),...來表示,只要這些采樣點的時間間隔Δt≤1/2F,便可根據各采樣值完全恢復原來的信號f(t)。
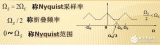
時域采樣定理的另一種表述方式是:當時間信號函數f(t)的最高頻率分量為fM時,f(t)的值可由一系列采樣間隔小于或等于1/2fM的采樣值來確定,即采樣點的重復頻率f≥2fM。圖為模擬信號和采樣樣本的示意圖。
時域采樣定理是采樣誤差理論、隨機變量采樣理論和多變量采樣理論的基礎。
頻域采樣定理 對于時間上受限制的連續信號f(t)(即當│t│>T時,f(t)=0,這里T=T2-T1是信號的持續時間),若其頻譜為F(ω),則可在頻域上用一系列離散的采樣值來表示,只要這些采樣點的頻率間隔ω≦π / tm 。
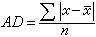
采樣簡介
從信號處理的角度來看,此采樣定理描述了兩個過程:其一是采樣,這一過程將連續時間信號轉換為離散時間信號;其二是信號的重建,這一過程離散信號還原成連續信號。
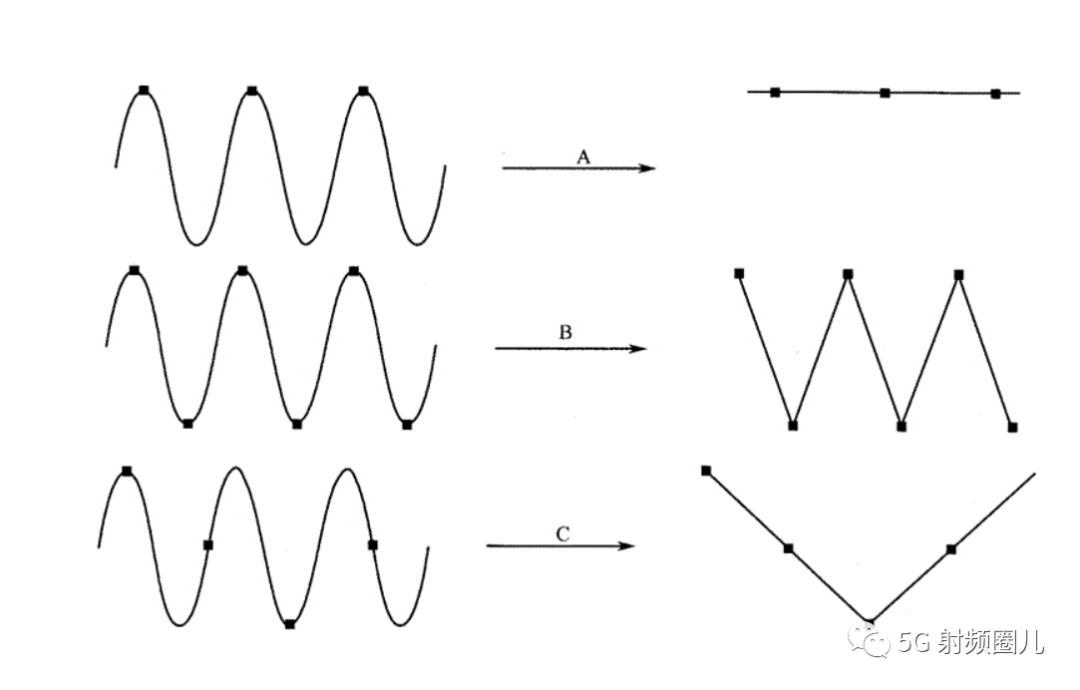
連續信號在時間(或空間)上以某種方式變化著,而采樣過程則是在時間(或空間)上,以T為單位間隔來測量連續信號的值。T稱為采樣間隔。在實際中,如果信號是時間的函數,通常他們的采樣間隔都很小,一般在毫秒、微秒的量級。采樣過程產生一系列的數字,稱為樣本。樣本代表了原來地信號。每一個樣本都對應著測量這一樣本的特定時間點,而采樣間隔的倒數,1/T即為采樣頻率,fs,其單位為樣本/秒,即赫茲(hertz)。
信號的重建是對樣本進行插值的過程,即,從離散的樣本x[n]中,用數學的方法確定連續信號x(t)。
從采樣定理中,我們可以得出以下結論:
如果已知信號的最高頻率fH,采樣定理給出了保證完全重建信號的最低采樣頻率。這一最低采樣頻率稱為臨界頻率或奈奎斯特采樣率,通常表示為fN。
相反,如果已知采樣頻率,采樣定理給出了保證完全重建信號所允許的最高信號頻率。
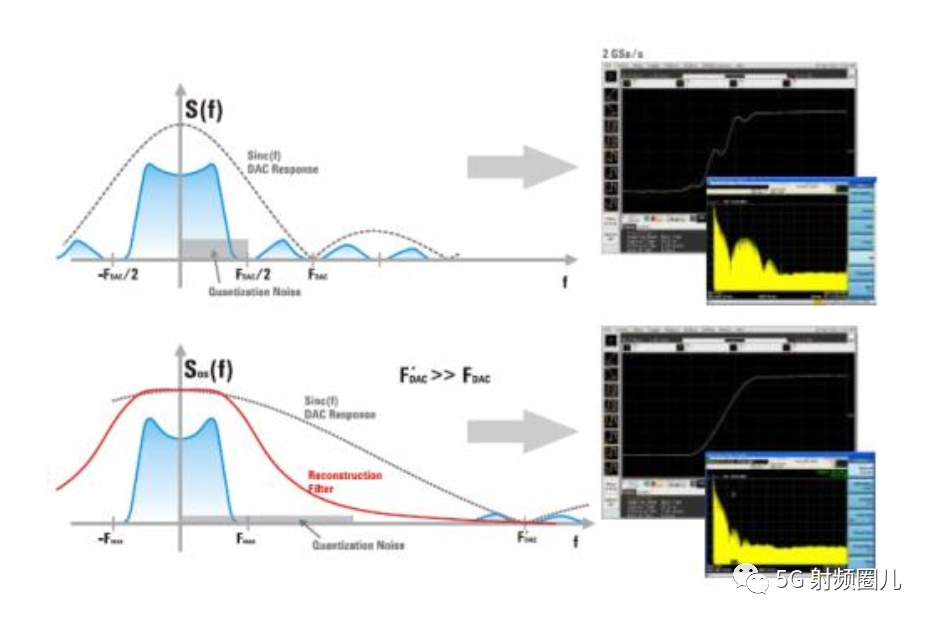
以上兩種情況都說明,被采樣的信號必須是帶限的,即信號中高于某一給定值的頻率成分必須是零,或至少非常接近于零,這樣在重建信號中這些頻率成分的影響可忽略不計。在第一種情況下,被采樣信號的頻率成分已知,比如聲音信號,由人類發出的聲音信號中,頻率超過5 kHz的成分通常非常小,因此以10 kHz的頻率來采樣這樣的音頻信號就足夠了。在第二種情況下,我們得假設信號中頻率高于采樣頻率一半的頻率成分可忽略不計。這通常是用一個低通濾波器來實現的。
混疊
如果不能滿足上述采樣條件,采樣后信號的頻率就會重疊,即高于采樣頻率一半的頻率成分將被重建成低于采樣頻率一半的信號。這種頻譜的重疊導致的失真稱為混疊,而重建出來的信號稱為原信號的混疊替身,因為這兩個信號有同樣的樣本值。
一個頻率正好是采樣頻率一半的弦波信號,通常會混疊成另一相同頻率的波弦信號,但它的相位和幅度改變了。以下兩種措施可避免混疊的發生:
1. 提高采樣頻率,使之達到最高信號頻率的兩倍以上;
2. 引入低通濾波器或提高低通濾波器的參數;該低通濾波器通常稱為抗混疊濾波器
抗混疊濾波器可限制信號的帶寬,使之滿足采樣定理的條件。從理論上來說,這是可行的,但是在實際情況中是不可能做到的。因為濾波器不可能完全濾除奈奎斯特頻率之上的信號,所以,采樣定理要求的帶寬之外總有一些“小的”能量。不過抗混疊濾波器可使這些能量足夠小,以至可忽略不計。
減采樣
當一個信號被減采樣時,必須滿足采樣定理以避免混疊。為了滿足采樣定理的要求,信號在進行減采樣操作前,必須通過一個具有適當截止頻率的低通濾波器。這個用于避免混疊的低通濾波器,稱為抗混疊濾波器。
定理
為了不失真地恢復模擬信號,采樣頻率應該大于模擬信號頻譜中最高頻率的2倍。
Fs>2Fmax
采樣率越高,稍后恢復出的波形就越接近原信號,但是對系統的要求就更高,轉換電路必須具有更快的轉換速度。
信號重構
任何信號都可以看做是不同頻率的正弦(余弦)信號的疊加,因此如果知道所有組成這一信號的正(余弦)信號的幅值、頻率和相角,就可以重構原信號。由于信號測量、分解及時頻變換的過程中存在誤差,因此不能100%地重構原信號,重構的信號只能保證原信號誤差在容許范圍內。

香農極限
信道的香農極限(或稱香農容量)指的是在會隨機發生誤碼的信道上進行無差錯傳輸的最大傳輸速率。它的存在是香農定理在帶寬有限的信道上的一個結論。
簡介
信道的香農極限(或稱香農容量)指的是在會隨機發生誤碼的信道上進行無差錯傳輸的最大傳輸速率。它的存在是香農定理在帶寬有限的信道上的一個結論。
有噪信道編碼定理
在信息論里,有噪信道編碼定理指出,盡管噪聲會干擾通信信道,但還是有可能在信息傳輸速率小于信道容量的前提下,以任意低的錯誤概率傳送數據信息。這個令人驚訝的結果,有時候被稱為信息原理基本定理,也叫做香農-哈特利定理或香農定理,是由克勞德·艾爾伍德·香農于1948年首次提出。
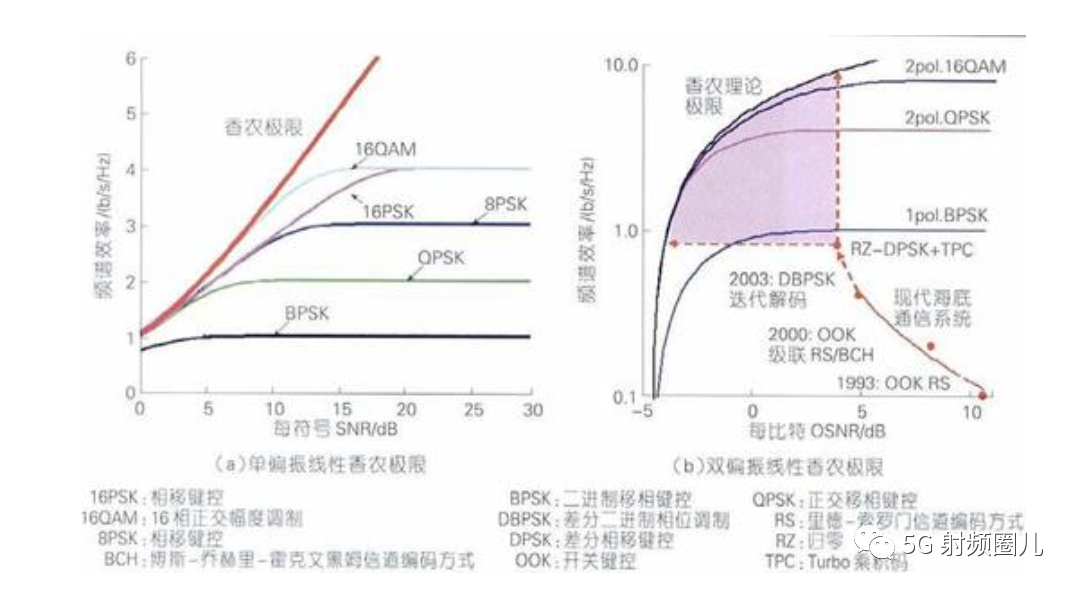
通信信道的信道容量或香農限制是指在指定的噪音標準下,信道理論上的最大傳輸率。
根據香農1948年的陳述,本定理描述了在不同級別的噪音干擾和數據損壞情況下,錯誤監測和糾正可能達到的最高效率。定理沒有指出如何構造錯誤監測的模型,只是告訴大家有可能達到的最佳效果。香農定理可以廣泛應用在通信和數據存儲領域。本定理是現代信息論的基礎理論。香農只是提出了證明的大概提綱。1954年,艾米爾·范斯坦第一個提出了嚴密的論證。
香農定理假設一個有噪音的信道,信道容量為C,信息以速度R傳送,如果
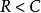
那么就存在一種編碼技術使接收端收到的錯誤達到任意小的數值。這意味著理論上,有可能無錯誤地傳送信息直到達到速度限制C。
反過來同樣重要。如果

那么想達到任意小的錯誤率是不可能實現的。因此,在傳送速度超過信道容量的時候,可靠傳輸信息是不能被保證的。定理并沒有指出在什么特殊情況下速度和容量相等。
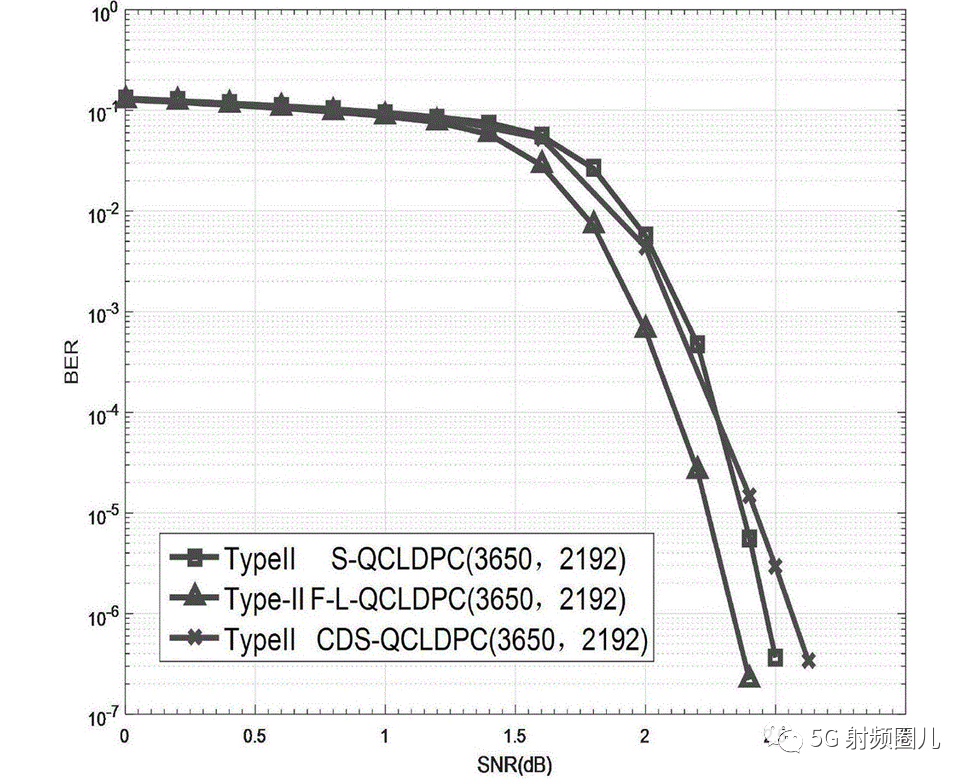
簡單的流程如"重復發送數據3遍,用一個投票系統在數據不一樣的時候選擇3個里面相同的那兩個的值"是低效的錯誤糾正的方式,不能保證數據塊能完全沒有錯誤地傳送。先進一些的技術如里德-所羅門碼編碼技術和更現代一些的Turbo碼、LDPC碼等編碼技術更逼近香農限制,但是計算復雜度很高。[1]?
理想加白噪聲情況下香農限
考慮數據率、噪聲以及誤碼率的關系。噪聲的存在會破壞一個或多個比特。假如數據率增加,那么這些比特會變短,因而給定的噪聲模式會影響更多個比特。于是,給定一個噪聲值,數據率越高則誤碼率也越高。所有的這些概念可以通過香農公式清楚聯系在一起,此公式由數學家克勞德·艾爾伍德·香農(Claude Elwood Shannon,1916-2001)推導得出的。
如剛才所描繪的,數據率越高,無用的噪聲會帶來更嚴重的破壞。在噪聲存在的情況下,給點一個噪聲值,我們能夠通過提高信號強度來提高正確接收數據的能力。在這一推導過程中涉及的主要參數是信噪比(SNR或S/N),它是指在傳輸過程中某一點的信號功率與噪聲包含功率之比。通常信噪比在接收器處測量,因為正是在這里我們試圖處理信號并消除無用噪聲。為了使用方便,這個比率通常用分貝表示
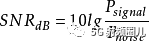
它表示有用信號超出噪聲值的量,以分貝為單位。SNR的值越高,表示信號的質量越好,所需中間轉發器的數量越少。
信噪比對數字數據傳輸十分重要,因為它限定了一個可達到的數據率上限。香農得出的結果是,用bps來表示的信道的最大容量遵從等式
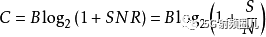
C是以比特/秒為單位的信道容量,凈比特率的理論上限(信息速率,有時表示為I),不包括糾錯碼;
B是帶寬的信道的在赫茲(通帶中的帶通信號的情況下的帶寬);
S是以瓦(或伏平方)測量的帶寬上的平均接收信號功率(在載波調制通帶傳輸的情況下,通常表示為C);
N是噪聲和帶寬上的干擾的平均功率,以瓦(或伏特平方)為單位測量;
S / N是通信信號對接收機噪聲和干擾的信噪比(SNR)或載波噪聲比(CNR)(表示為線性功率比,而不是對數分貝) 。
香農公式顯示出理論上可達到的最大值。然而在實際應用中能夠達到的速率要低得多。其中一個原因是該公式假定噪聲為白噪聲(熱噪聲),既沒有考慮到沖激噪聲,也沒有考慮衰減和時延失真。即使在理想白噪聲情況下,因為編碼的原因(如編碼長度和復雜性等),目前的技術仍然無法達到香農容量。
香農公式中提到的容量為無誤碼容量。經香農證明,假如信道上的實際信息率比無誤碼容量低,從理論上來說,通過適當的信息編碼,信道就有可能達到無誤碼容量。遺憾的是,香農的理論并沒有給出如何找到這種編碼的方法,但提供了一個用來衡量實際通信機制性能的計算標準。
通過香農公式我們可以考慮如何將信道容量上限提高。假如噪聲值給定,那么似乎通過增加信號強度或帶寬就能提高數據率;但是,如果信號強度增加了,則系統的非線性程度也會提高,這就導致互調噪聲的增加。還有一點需要注意,由于假定噪聲是白噪聲,那么帶寬越寬,因此系統容納的噪聲也就越多,因此隨著B的增加SNR反而降低了。
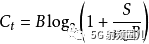
當
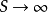
,或
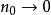
時,
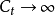
。
但是當
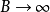
時,
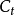
將趨向何值?
令
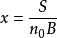
,上式可以改寫為:
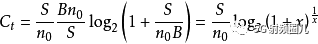
利用關系式:
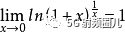
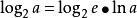
上式變為:
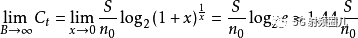
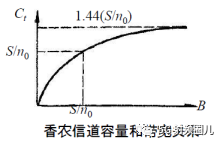
上式表明,當給定
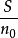
時,若帶寬B趨于無窮大,信道容量不會趨于無限大,而只是
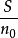
的1.44倍。這是
因為當帶寬B增大時,噪聲功率也隨之增大。
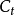
和帶寬B的關系曲線:
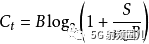
上式還可以改寫成如下形式:
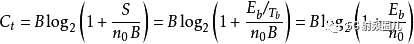
式中
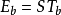
——每比特能量

——每比特持續時間
上式表明,為了得到給定的信道容量
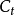
,可以增大帶寬B以換取
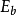
的減小;另一方面,在接收功率受 限的情況下,由于
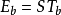
,可以增大
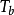
以減小S來保持
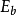
和
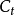
不變。
香農哈特利定律
在信息論中,香農極限告訴在該信息可以通過一個特定帶寬的存在特定噪聲的通信信道數據被發送的最大速率。這是噪聲信道編碼定理在受到高斯噪聲的連續時間、模擬通信信道的原型情況下的應用。該定理建立了對這種通信鏈路的信道香農限,限制了在存在噪聲干擾的情況下可以以指定帶寬發送的每個時間單位的無錯誤信息的最大量,假設信號功率是有界的,并且高斯噪聲過程的特征在于已知功率或功率譜密度。定理以Claude Shannon和Ralph Hartley命名。
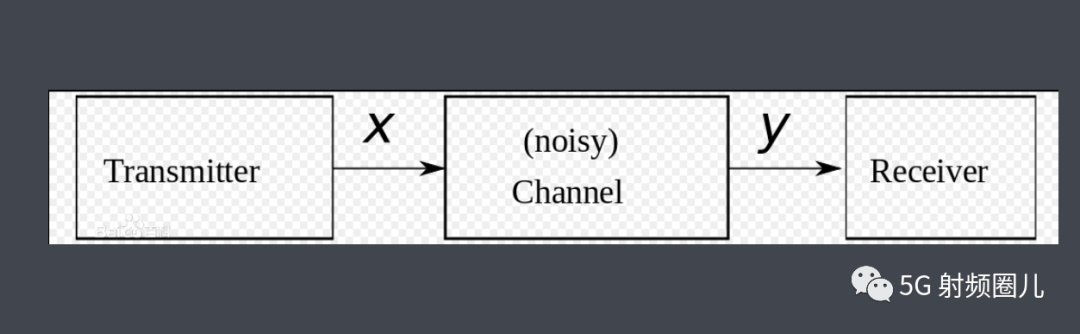
香農 - 哈特利定理陳述了通道容量C,這意味著可以使用平均接收信號功率S通過經過加性白高斯的模擬通信通道以任意低的錯誤率傳送的數據的信息速率的理論上的最上限電源噪聲N:
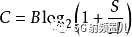
奈奎斯特率
在1927年,奈奎斯特認為每單位時間可以通過電報通道的獨立脈沖數量被限制在通道帶寬的兩倍。在符號中,
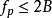
其中
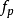
是脈沖頻率(以每秒脈沖數計),B是帶寬(赫茲)。數量2B后來被稱為奈奎斯特速率,并以每秒2個B脈沖的限制脈沖速率以奈奎斯特率發送信號。奈奎斯特在1928年發表他的研究成果,作為他的論文“電訊傳播理論中的某些話題”的一部分。
哈特利定律
1928年,哈特利制定了一種量化信息和線路速率(也稱為數據信令速率 R比特每秒)的方法。這種方法,后來被稱為哈特利定律,成為香農更加復雜的通道容量概念的重要前身。
哈特利認為,可以通過通信信道可靠地發送和接收的可區分脈沖電平的最大數量受到信號幅度的動態范圍和接收機能夠區分振幅電平的精度的限制。具體地說,如果發送信號的幅度被限制在[ - A ... + A ]伏的范圍內,并且接收機的精度為± ΔV伏特,則不同脈沖M的最大數量由
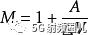
通過以比特/脈沖中的每個脈沖獲取信息作為可以發送的不同消息M的數量的基2-對數,Hartley構建了線速率R的度量:
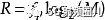
,
其中
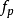
是脈沖速率,也稱為符號速率,以符號/秒或波特率表示。
然后,哈特利將上述量化與奈奎斯特的觀察結合起來,可以通過帶寬B 赫茲通道的獨立脈沖數為每秒2B脈沖,以達到其可實現線速率的定量測量。
哈特利定律有時引述只是模擬帶寬,B,以Hz為單位,和今天被稱為數字帶寬的R ,以比特/秒為單位之間的比例。其他時候,以這種更定量的形式引用,作為每秒可用的R比特率:
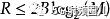
哈特利沒有確切地知道數字M應如何依賴于信道的噪聲統計,或者即使單個符號脈沖不能可靠地區分為M個等級,通信如何可靠地生成; 利用高斯噪聲統計,系統設計人員必須選擇非常保守的M值來實現低錯誤率。
哈特利的速率結果可以被看作是一個無差錯的能力中號的2個進制信道B每秒符號。有些作者將其稱為容量。但是這樣一個無誤的信道是一個理想化的方式,如果選擇M小到足以使噪聲信道幾乎無誤,結果必然小于帶寬B的噪聲信道的香農容量,這是隨后的香農哈特利定律結果后來。
哈特利定律與香農限的關系
將信道容量與哈特利定律的信息比率進行比較,我們可以找到有效數量的可區分級別M:
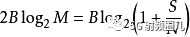
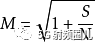
平方根有效地將功率比轉換回電壓比,因此電平數量幾乎與信號RMS幅度與噪聲標準偏差之比成正比。香農限與哈特利定律之間形式的相似性不應該被解釋為意味著M脈沖水平可以毫無混亂地被發送; 需要更多的級別,以允許冗余編碼和糾錯,但是可以用編碼處理的凈數據速率等同于使用哈特利定律中的M。
可替代形式
頻率依賴(彩色噪聲)情況
在上面的簡單版本中,信號和噪聲完全不相關,在這種情況下,S + N是接收信號和噪聲的總功率。通過對多個窄獨立的高斯信道并行處理信道,獲得加性噪聲不是白色(或S / N在帶寬上的頻率不恒定)的情況下的上述等式的推廣,
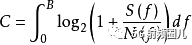
C是以比特/秒為單位的信道容量 ;
B是信道的帶寬,單位為Hz;
S(f)是信號功率譜
N(f)是噪聲功率譜
f是以Hz為單位的頻率。
注意:該定理僅適用于高斯穩定過程噪聲。該公式引入頻率相關噪聲的方法不能描述所有的連續時間噪聲過程。例如,考慮噪聲過程,其包括在任何時間點加上振幅為1或-1的隨機波,以及將這樣的波加到源信號上的信道。這樣的波的頻率分量是高度依賴的。雖然這樣的噪聲可能具有高功率,但是如果底層噪聲是每個頻帶中的獨立噪聲之和,則傳輸比所需要的功率少得多的連續信號是相當容易的。
近似
對于大或小且恒定的信噪比,容量公式(香農公式)可以近似為:
如果S / N >> 1,那么
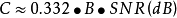
這里
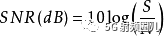
2. 同理,如果S / N <<1,那么
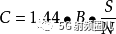
?
在這種低SNR近似中,如果噪聲為白色,則光譜密度的容量與帶寬無關
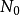
瓦特/赫茲,在這種情況下,總 噪聲功率是
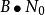
。

非靜止記憶信道的信道容量
編輯
假設通道是無記憶的,但是其轉換概率隨時間而變化,以發射機和接收機已知的方式。然后通道容量由
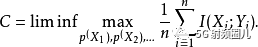
在每個相應通道的容量達到分配的情況下達到最大值。也就是,
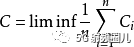
這里
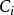
代表第i個信道的容量。[1]
?
各種編碼對于接近香農限的程度
諸如“發送消息3次并且如果副本不同則使用最佳2投票方案”這樣的簡單方案是無效率的糾錯方法,不能夠漸近地保證一個數據塊可以毫無差錯地傳達。諸如Reed-Solomon碼的高級技術,以及最近的低密度奇偶校驗(LDPC)碼和turbo碼更接近于達到理論香農限制,但是以高的計算復雜度為代價。使用這些高效率的代碼和當今數字信號處理器的計算能力,現在可以達到非常接近香農限額。實際上,已經表明,LDPC碼可以達到香農極限的0.0045dB(對于二進制AWGN信道,具有非常長的塊長度)。
土耳其畢爾肯大學教授Erdal Arikan于2009年正式提出的新型編碼方案——極化碼(polar code),是目前唯一一個在理論上已經被證明可以到達香農限的方案。
編輯:黃飛
?
 電子發燒友App
電子發燒友App









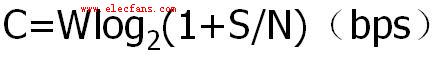












評論