找出與反射系數(shù)對應(yīng)的元件值(尤其是匹配網(wǎng)絡(luò)的元件,見圖7)
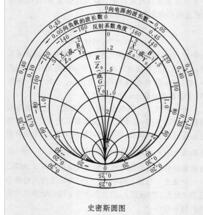
推論因為史密斯圓圖是一種基于圖形的解法,所得結(jié)果的精確度直接依賴于圖形的精度下面是一個用史密斯圓圖表示的RF應(yīng)用實例:例: 已知特性阻抗為50,負載阻抗如下:
Z1 = 100 + j50 Z2 = 75 - j100 Z3 = j200 Z4 = 150
Z5 = (開路) Z6 = 0 (短路) Z7 = 50 Z8 = 184 - j900
對上面的值進行歸一化并標(biāo)示在圓圖中(見圖5):
z1 = 2 + j z2 = 1.5 - j2 z3 = j4 z4 = 3
z5 = 8 z6 = 0 z7 = 1 z8 = 3.68 - j18
點擊看大圖(PDF, 502K)
圖5. 史密斯圓圖上的點
現(xiàn)在可以通過圖5的圓圖直接解出反射系數(shù)畫出阻抗點(等阻抗圓和等電抗圓的交點),只要讀出它們在直角坐標(biāo)水平軸和垂直軸上的投影,就得到了反射系數(shù)的實部r和虛部i (見圖6)
該范例中可能存在八種情況,在圖6所示史密斯圓圖上可以直接得到對應(yīng)的反射系數(shù):
1 = 0.4 + 0.2j 2 = 0.51 - 0.4j 3 = 0.875 + 0.48j 4 = 0.5
5 = 1 6 = -1 7 = 0 8 = 0.96 - 0.1j
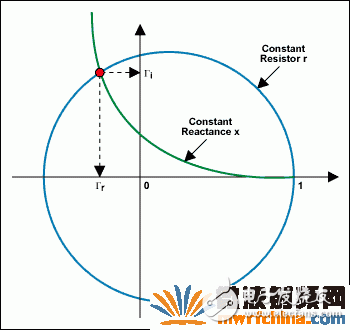
圖6. 從X-Y軸直接讀出反射系數(shù)的實部和虛部用導(dǎo)納表示史密斯圓圖是用阻抗(電阻和電抗)建立的一旦作出了史密斯圓圖,就可以用它分析串聯(lián)和并聯(lián)情況下的參數(shù)可以添加新的串聯(lián)元件,確定新增元件的影響只需沿著圓周移動到它們相應(yīng)的數(shù)值即可然而,增加并聯(lián)元件時分析過程就不是這么簡單了,需要考慮其它的參數(shù)通常,利用導(dǎo)納更容易處理并聯(lián)元件
我們知道,根據(jù)定義Y = 1/Z,Z = 1/Y導(dǎo)納的單位是姆歐或者-1 (早些時候?qū)Ъ{的單位是西門子或S)并且,如果Z是復(fù)數(shù),則Y也一定是復(fù)數(shù)
所以Y = G + jB (2.20), 其中G叫作元件的電導(dǎo),B稱電納在演算的時候應(yīng)該小心謹慎,按照似乎合乎邏輯的假設(shè),可以得出:G = 1/R及B = 1/X,然而實際情況并非如此,這樣計算會導(dǎo)致結(jié)果錯誤
用導(dǎo)納表示時,第一件要做的事是歸一化, y = Y/Y0,得出y = g + jb但是如何計算反射系數(shù)呢?通過下面的式子進行推導(dǎo):
結(jié)果是G的表達式符號與z相反,并有(y) = -(z)
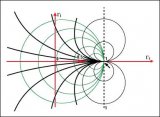
如果知道z,就能通過將的符號取反找到一個與(0, 0)的距離相等但在反方向的點圍繞原點旋轉(zhuǎn)180°可以得到同樣的結(jié)果(見圖7)

圖7. 180°度旋轉(zhuǎn)后的結(jié)果
當(dāng)然,表面上看新的點好像是一個不同的阻抗,實際上Z和1/Z表示的是同一個元件(在史密斯圓圖上,不同的值對應(yīng)不同的點并具有不同的反射系數(shù),依次類推)出現(xiàn)這種情況的原因是我們的圖形本身是一個阻抗圖,而新的點代表的是一個導(dǎo)納因此在圓圖上讀出的數(shù)值單位是姆歐
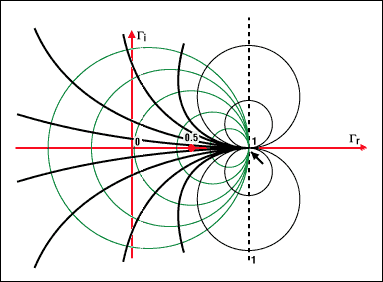
盡管用這種方法就可以進行轉(zhuǎn)換,但是在解決很多并聯(lián)元件電路的問題時仍不適用導(dǎo)納圓圖在前面的討論中,我們看到阻抗圓圖上的每一個點都可以通過以復(fù)平面原點為中心旋轉(zhuǎn)180°后得到與之對應(yīng)的導(dǎo)納點于是,將整個阻抗圓圖旋轉(zhuǎn)180°就得到了導(dǎo)納圓圖這種方法十分方便,它使我們不用建立一個新圖所有圓周的交點(等電導(dǎo)圓和等電納圓)自然出現(xiàn)在點(-1, 0)使用導(dǎo)納圓圖,使得添加并聯(lián)元件變得很容易在數(shù)學(xué)上,導(dǎo)納圓圖由下面的公式構(gòu)造:
解這個方程
接下來,令方程3.3的實部和虛部相等,我們得到兩個新的獨立的關(guān)系:
從等式3.4,我們可以推導(dǎo)出下面的式子:

它也是復(fù)平面(r, i)上圓的參數(shù)方程(x-a)² + (y-b) ² = R² (方程3.12),以(-g/g+1, 0)為圓心,半徑為1/(1+g)
從等式3.5,我們可以推導(dǎo)出下面的式子:
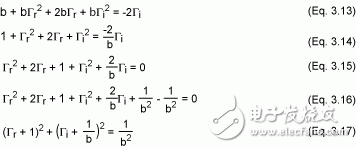
同樣得到(x-a)² + (y-b)² = R²型的參數(shù)方程(方程3.17)求解等效阻抗當(dāng)解決同時存在串聯(lián)和并聯(lián)元件的混合電路時,可以使用同一個史密斯圓圖,在需要進行從z到y(tǒng)或從y到z的轉(zhuǎn)換時將圖形旋轉(zhuǎn)
考慮圖8所示網(wǎng)絡(luò)(其中的元件以Z0 = 50進行了歸一化)串聯(lián)電抗(x)對電感元件而言為正數(shù),對電容元件而言為負數(shù)而電納(b)對電容元件而言為正數(shù),對電感元件而言為負數(shù)
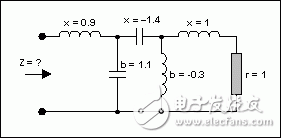
圖8. 一個多元件電路
這個電路需要進行簡化(見圖9)從最右邊開始,有一個電阻和一個電感,數(shù)值都是1,我們可以在r = 1的圓周和I=1的圓周的交點處得到一個串聯(lián)等效點,即點A下一個元件是并聯(lián)元件,我們轉(zhuǎn)到導(dǎo)納圓圖(將整個平面旋轉(zhuǎn)180°),此時需要將前面的那個點變成導(dǎo)納,記為A'現(xiàn)在我們將平面旋轉(zhuǎn)180°,于是我們在導(dǎo)納模式下加入并聯(lián)元件,沿著電導(dǎo)圓逆時針方向(負值)移動距離0.3,得到點B然后又是一個串聯(lián)元件現(xiàn)在我們再回到阻抗圓圖
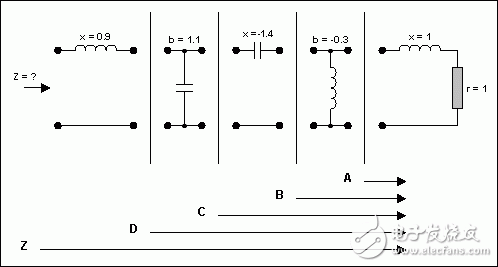
圖9. 將圖8網(wǎng)絡(luò)中的元件拆開進行分析
在返回阻抗圓圖之前,還必需把剛才的點轉(zhuǎn)換成阻抗(此前是導(dǎo)納),變換之后得到的點記為B',用上述方法,將圓圖旋轉(zhuǎn)180°回到阻抗模式沿著電阻圓周移動距離1.4得到點C就增加了一個串聯(lián)元件,注意是逆時針移動(負值)進行同樣的操作可增加下一個元件(進行平面旋轉(zhuǎn)變換到導(dǎo)納),沿著等電導(dǎo)圓順時針方向(因為是正值)移動指定的距離(1.1)這個點記為D最后,我們回到阻抗模式增加最后一個元件(串聯(lián)電感)于是我們得到所需的值,z,位于0.2電阻圓和0.5電抗圓的交點至此,得出z = 0.2 + j0.5如果系統(tǒng)的特性阻抗是50,有Z = 10 + j25 (見圖10)
點擊看大圖(PDF, 600K)
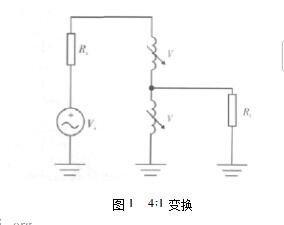
圖10. 在史密斯圓圖上畫出的網(wǎng)絡(luò)元件逐步進行阻抗匹配史密斯圓圖的另一個用處是進行阻抗匹配這和找出一個已知網(wǎng)絡(luò)的等效阻抗是相反的過程此時,兩端(通常是信號源和負載)阻抗是固定的,如圖11所示我們的目標(biāo)是在兩者之間插入一個設(shè)計好的網(wǎng)絡(luò)已達到合適的阻抗匹配
圖11. 阻抗已知而元件未知的典型電路
初看起來好像并不比找到等效阻抗復(fù)雜但是問題在于有無限種元件的組合都可以使匹配網(wǎng)絡(luò)具有類似的效果,而且還需考慮其它因素(比如濾波器的結(jié)構(gòu)類型品質(zhì)因數(shù)和有限的可選元件)
實現(xiàn)這一目標(biāo)的方法是在史密斯圓圖上不斷增加串聯(lián)和并聯(lián)元件直到得到我們想要的阻抗從圖形上看,就是找到一條途徑來連接史密斯圓圖上的點同樣,說明這種方法的最好辦法是給出一個實例
我們的目標(biāo)是在60MHz工作頻率下匹配源阻抗(ZS)和負載阻抗(zL) (見圖11)網(wǎng)絡(luò)結(jié)構(gòu)已經(jīng)確定為低通,L型(也可以把問題看作是如何使負載轉(zhuǎn)變成數(shù)值等于ZS的阻抗,即ZS復(fù)共軛)下面是解的過程:
點擊看大圖(PDF, 537K)
圖12. 圖11的網(wǎng)絡(luò),將其對應(yīng)的點畫在史密斯圓圖上
要做的第一件事是將各阻抗值歸一化如果沒有給出特性阻抗,選擇一個與負載/信號源的數(shù)值在同一量級的阻抗值假設(shè)Z0為50于是zS = 0.5 - j0.3, z*S = 0.5 + j0.3, ZL = 2 - j0.5
下一步,在圖上標(biāo)出這兩個點,A代表zL,D代表z*S
然后判別與負載連接的第一個元件(并聯(lián)電容),先把zL轉(zhuǎn)化為導(dǎo)納,得到點A'
確定連接電容C后下一個點出現(xiàn)在圓弧上的位置由于不知道C的值,所以我們不知道具體的位置,然而我們確實知道移動的方向并聯(lián)的電容應(yīng)該在導(dǎo)納圓圖上沿順時針方向移動直到找到對應(yīng)的數(shù)值,得到點B (導(dǎo)納)下一個元件是串聯(lián)元件,所以必需把B轉(zhuǎn)換到阻抗平面上去,得到B'B'必需和D位于同一個電阻圓上從圖形上看,從A'到D只有一條路徑,但是如果要經(jīng)過中間的B點(也就是B'),就需要經(jīng)過多次的嘗試和檢驗在找到點B和B'后,我們就能夠測量A'到B和B'到D的弧長,前者就是C的歸一化電納值,后者為L的歸一化電抗值A(chǔ)'到B的弧長為b = 0.78,則B = 0.78 x Y0 = 0.0156姆歐因為
C = B,所以C = B/ = B/(2 f) = 0.0156/(2 607) = 41.4pF
B到D的弧長為x = 1.2,于是X = 1.2 x Z0 = 60 由L = X, 得L = X/ = X/(2 f)= 60/(2 607) = 159nH
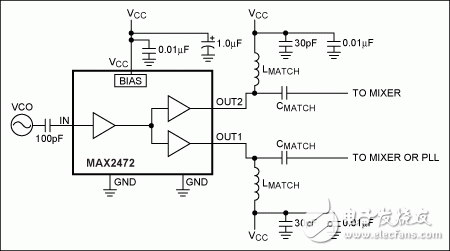
圖13. MAX2472典型工作電路
第二個例子是MAX2472的輸出匹配電路,匹配于50負載阻抗(zL),工作品率為900MHz (圖14所示)該網(wǎng)絡(luò)采用與MAX2472數(shù)據(jù)資料相同的配置結(jié)構(gòu),上圖給出了匹配網(wǎng)絡(luò),包括一個并聯(lián)電感和串聯(lián)電容,以下給出了匹配網(wǎng)絡(luò)元件值的查找過程
圖14. 圖13所示網(wǎng)絡(luò)在史密斯圓a圖上的相應(yīng)工作點
首先將S22散射參數(shù)轉(zhuǎn)換成等效的歸一化源阻抗MAX2472的Z0為50,S22 = 0.81/-29.4°轉(zhuǎn)換成zS = 1.4 - j3.2, zL = 1和zL* = 1
下一步,在圓圖上定位兩個點,zS標(biāo)記為A,zL*標(biāo)記為D因為與信號源連接的是第一個元件是并聯(lián)電感,將源阻抗轉(zhuǎn)換成導(dǎo)納,得到點A
確定連接電感LMATCH后下一個點所在的圓弧,由于不知道LMATCH的數(shù)值,因此不能確定圓弧終止的位置但是,我們了解連接LMATCH并將其轉(zhuǎn)換成阻抗后,源阻抗應(yīng)該位于r = 1的圓周上由此,串聯(lián)電容后得到的阻抗應(yīng)該為z = 1 + j0以原點為中心,在r = 1的圓上旋轉(zhuǎn)180°,反射系數(shù)圓和等電納圓的交點結(jié)合A點可以得到B (導(dǎo)納)B點對應(yīng)的阻抗為B點
找到B和B'后,可以測量圓弧A'B以及圓弧B'D的長度,第一個測量值可以得到LMATCH電納的歸一化值,第二個測量值得到CMATCH電抗的歸一化值圓弧A'B的測量值為b = -0.575,B = -0.575 × Y0 = 0.0115mhos因為1/L = B,則LMATCH = 1/B = 1/(B2 f) = 1/(0.01156 × 2 × × 900 × 106) = 15.38nH,近似為15nH圓弧B'D的測量值為X = -2.81,X = -2.81 × Z0 = -140.5因為-1/C = X,則CMATCH = -1/X = -1/(X2 f) = -1/(-140.5 × 2 × × 900 × 106) = 1.259pF,近似為1pF這些計算值沒有考慮寄生電感和寄生電容,所得到的數(shù)值接近與數(shù)據(jù)資料中給出的數(shù)值: LMATCH = 12nH和CMATCH = 1pF
總結(jié)在擁有功能強大的軟件和高速高性能計算機的今天,人們會懷疑在解決電路基本問題的時候是否還需要這樣一種基礎(chǔ)和初級的方法
實際上,一個真正的工程師不僅應(yīng)該擁有理論知識,更應(yīng)該具有利用各種資源解決問題的能力在程序中加入幾個數(shù)字然后得出結(jié)果的確是件容易的事情,當(dāng)問題的解十分復(fù)雜并且不唯一時,讓計算機作這樣的工作尤其方便然而,如果能夠理解計算機的工作平臺所使用的基本理論和原理,知道它們的由來,這樣的工程師或設(shè)計者就能夠成為更加全面和值得信賴的專家,得到的結(jié)果也更加可靠
 電子發(fā)燒友App
電子發(fā)燒友App









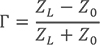














評論