這篇文章非常詳細(xì)的講解了寬帶分相網(wǎng)絡(luò)（或移相網(wǎng)絡(luò)、多項(xiàng)網(wǎng)絡(luò)）的設(shè)計(jì)，這個(gè)設(shè)計(jì)是現(xiàn)有分相網(wǎng)絡(luò)的雛形，其基本理論和推導(dǎo)方法非常經(jīng)典，以供學(xué)習(xí)參考。

本文發(fā)表時(shí)間是1950年，作者W. Saraga 是一位德國(guó)猶太物理學(xué)家，出生于柏林，父親是羅馬尼亞人，母親是俄羅斯人。

The Design of Wide-Band Phase Splitting Networks*

寬帶分相網(wǎng)絡(luò)設(shè)計(jì)*

W. SARAGA?, SENIOR MEMBER, IRE

摘要

近年來(lái)，已有許多文章和專利討論了分相網(wǎng)絡(luò)的性質(zhì)和設(shè)計(jì)，特別是與單邊帶調(diào)制器配合使用的情況。然而，它們都限制在特定的設(shè)計(jì)方法或特定數(shù)量的設(shè)計(jì)參數(shù)上。本文給出了對(duì)分相網(wǎng)絡(luò)的一般性研究結(jié)果，分別處理網(wǎng)絡(luò)分析、網(wǎng)絡(luò)綜合和性能曲線逼近問題。對(duì)于最重要類型的曲線逼近，如泰勒和切比雪夫逼近，給出了任意數(shù)量的設(shè)計(jì)參數(shù)和任意所需逼近精度的顯式公式。提供了經(jīng)典全通濾波網(wǎng)絡(luò)的替代方案，并且發(fā)展了損耗補(bǔ)償相移網(wǎng)絡(luò)。通過(guò)這種方式，提供了對(duì)復(fù)雜指標(biāo)的分相網(wǎng)絡(luò)的清晰和相對(duì)簡(jiǎn)單的設(shè)計(jì)指南。此外，我們相信其中一些提供的理論結(jié)果和開發(fā)的方法，例如，泰勒和切比雪夫逼近、損耗補(bǔ)償?shù)姆椒ā⒕W(wǎng)絡(luò)綜合的某種方法，以及將逼近曲線表示為兩個(gè)變量的迭代函數(shù)（迭代指數(shù)為分?jǐn)?shù)）是新穎且具有一般理論意義的。

I. 引言

過(guò)去十年間，經(jīng)常討論如何設(shè)計(jì)分相電路以在寬頻帶上產(chǎn)生恒定的相差。這些電路主要用于載波電話的單邊帶調(diào)制器、多相無(wú)線電系統(tǒng)、頻移鍵控以及陰極射線示波器的寬帶圓時(shí)基。

有趣的是，在早期提及信號(hào)頻帶分相的三個(gè)參考文獻(xiàn)中，沒有提供直接分相的寬帶網(wǎng)絡(luò)，而是使用了輔助的兩相單頻載波源，配合適當(dāng)?shù)恼{(diào)制器和解調(diào)器級(jí)聯(lián)。 (Wirkler,? Vilbig? )。早在1925年，Hartley? 描述了一個(gè)由兩個(gè)具有不同截止頻率和不同級(jí)數(shù)的濾波器組成的寬帶分相網(wǎng)絡(luò)。Honnell? 和 Lenehan? 描述了非常簡(jiǎn)單的寬帶分相電路，但沒有提供恒定幅度輸出。由Byrne?、Loyet?、Hodgson?、Dome?、Norgaard? 和 Luck? 描述的寬帶分相電路由兩個(gè)具有恒定輸出幅度的相移網(wǎng)絡(luò)組成。

Byrne和Loyet提供了各種分相電路的理論和測(cè)量的指標(biāo)性能，但沒有提供任何設(shè)計(jì)信息。另一方面，Hodgson詳細(xì)討論了設(shè)計(jì)方法。他的主要建議是分別設(shè)計(jì)每個(gè)相移網(wǎng)絡(luò)，以使其在相關(guān)頻帶上的相移與頻率的對(duì)數(shù)成線性關(guān)系，即，其中和是常數(shù)。如果對(duì)于兩個(gè)網(wǎng)絡(luò)是相同的，但對(duì)于每個(gè)網(wǎng)絡(luò)是不同的，比如和，那么兩個(gè)相移和的差值是，即為所需的常數(shù)。Dome遵循相同的一般思路，但Hodgson的討論主要是在格型和橋相移網(wǎng)絡(luò)方面，而Dome描述了一些對(duì)經(jīng)典格型網(wǎng)絡(luò)的有趣替代方案。在Hodgson的專利中，兩個(gè)相移網(wǎng)絡(luò)的個(gè)體性能是分別標(biāo)定的；Luck討論了分相電路的設(shè)計(jì)和性能作為一個(gè)整體。這是一個(gè)重要的進(jìn)步。但是，Luck只考慮了具有四個(gè)設(shè)計(jì)參數(shù)的網(wǎng)絡(luò)。

本文的目的是研究具有任意數(shù)量的設(shè)計(jì)參數(shù)、任意期望帶寬和任意接近期望理想性能的分相網(wǎng)絡(luò)。 行文將按以下順序進(jìn)行：(1)網(wǎng)絡(luò)分析，(2)性能曲線逼近，(3)網(wǎng)絡(luò)綜合。將發(fā)現(xiàn)獲得具有一般有效性和適用性的結(jié)果相對(duì)容易。在許多方面，需要解決的問題類似于或與在濾波器設(shè)計(jì)的綜合方法和理論開發(fā)中遇到的問題相同。然而，在由恒定阻抗電路組成的分相電路的情況下，解決這些問題比濾波器設(shè)計(jì)的情況更容易，因?yàn)椴粫?huì)出現(xiàn)不匹配所引起的復(fù)雜問題。此外，恰好在橢圓函數(shù)變換理論中，這對(duì)濾波器以及分相電路設(shè)計(jì)都適用，對(duì)于分相電路設(shè)計(jì)的變換比適用于濾波器設(shè)計(jì)的變換更簡(jiǎn)單。

II. 基本電路

圖1所示顯示了一個(gè)由兩個(gè)相移網(wǎng)絡(luò)組成的分相電路，它們?cè)谳斎攵瞬⒙?lián)。在我們研究的初期，假定相移網(wǎng)絡(luò)是傳統(tǒng)的全通恒阻單級(jí)點(diǎn)格型網(wǎng)絡(luò)，其串聯(lián)臂的電抗分別為? 和?，格臂的電抗分別為? 和?。

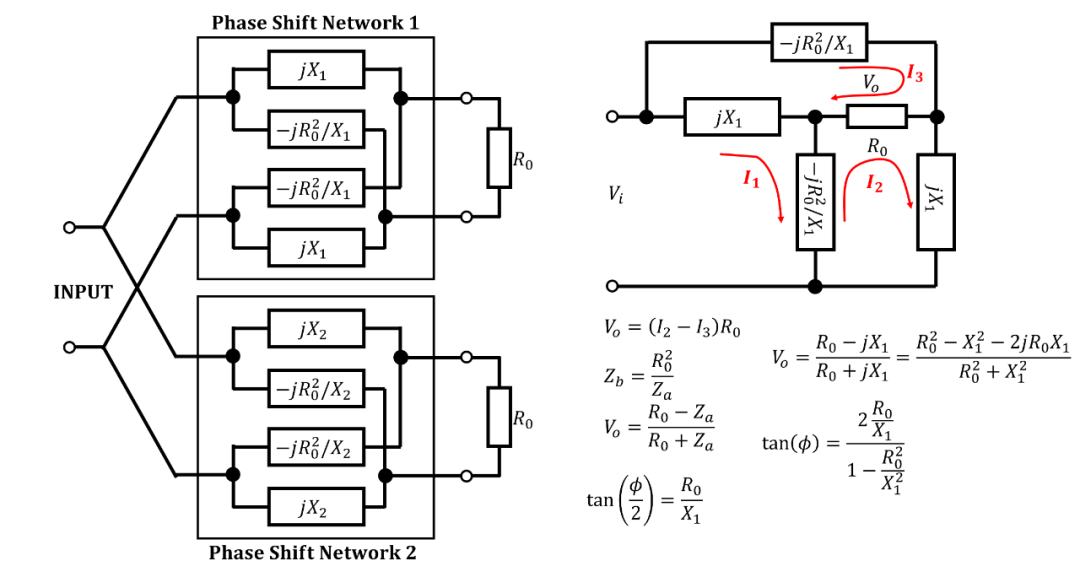
圖1. 基本的分相電路

譯注：圖1經(jīng)過(guò)重繪，右邊是對(duì)其中一個(gè)移相網(wǎng)絡(luò)進(jìn)行分析，經(jīng)過(guò)驗(yàn)證，角度公式和圖有出入，問題應(yīng)該在輸出的極性上，將電壓極性反轉(zhuǎn)就可以得到式(1)。

然后，網(wǎng)絡(luò)分別產(chǎn)生的相移? 和? 由以下公式給出

因此，相移差? 由以下公式給出

如果?，。因此，在理想的? 分相電路中， 應(yīng)為1，或?。

與1的偏差大小的重要性只能通過(guò)參考分相電路的特定應(yīng)用來(lái)討論。考慮使用分相網(wǎng)絡(luò)的單邊帶調(diào)制器是有意義的。如果假定所有幅度和相位關(guān)系都完全符合要求（見圖2），

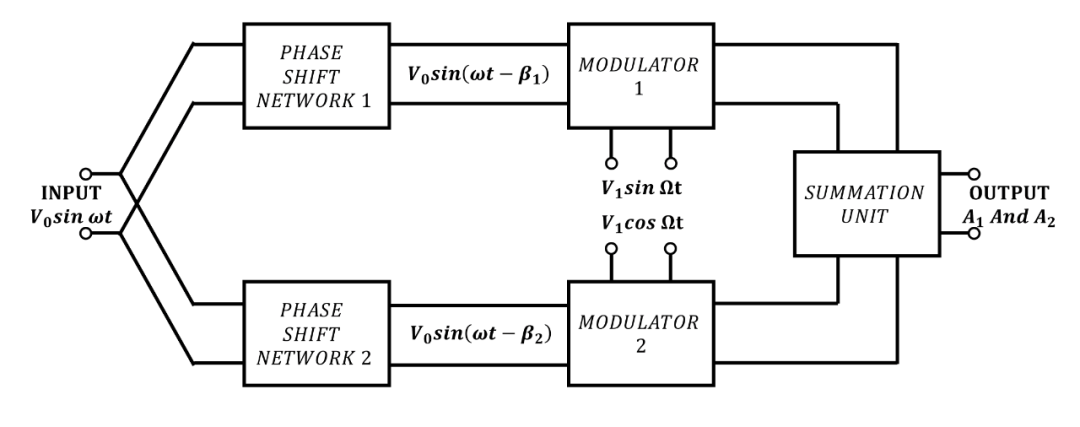
圖2. 使用分相電路的單邊帶調(diào)制器

但不完全為1，可以顯示所需的邊帶幅度? 和抑制的邊帶幅度? 由以下公式給出：

其中? 是相位差? 與? 的偏差，即

其中? 是? 時(shí)? 的值。

譯注：這里可以推導(dǎo)出總輸出公式：

代入式(4)得到：

式中求和第一項(xiàng)為上邊帶，也即所需邊帶(式(3a)中表示誤差對(duì)所需邊帶的抑制，越小越好)，第二項(xiàng)為下邊帶，即為所抑制的邊帶(式(3b)中表示誤差對(duì)抑制邊帶的抑制，越大越好)。將式(4)代入式(2)可以得到式(5):

如果給定了?，我們可以通過(guò)以下公式直接獲得? ：

將（3a）和（3b）與（5）結(jié)合起來(lái)，我們可以獲得? 和? 作為? 的函數(shù)。結(jié)果已在圖3中繪制。

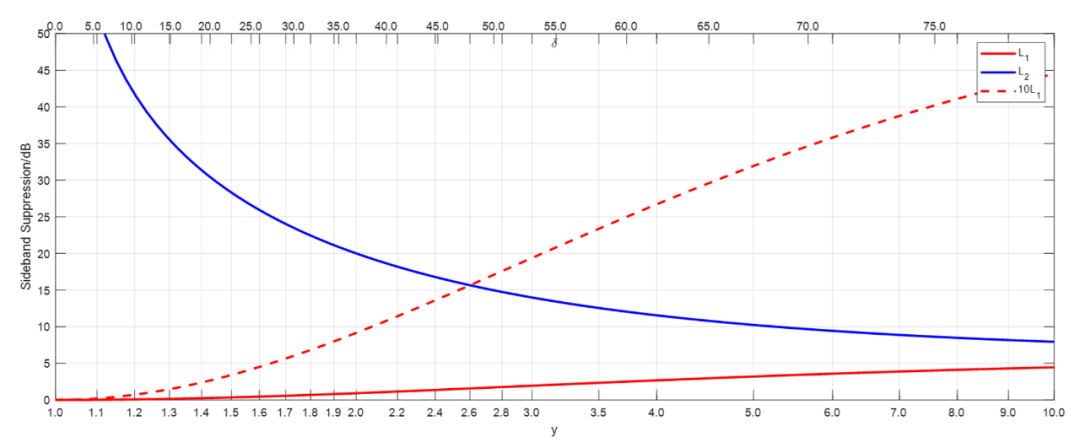
圖3. 輸出（所需和需抑制的邊帶）作為相位與? 偏差和的函數(shù)

要注意，轉(zhuǎn)換? 使? 和? 保持不變，并將? 轉(zhuǎn)換為?。

式（2）與源電阻? 和負(fù)載電阻? 之間的格型濾波器的插入損耗? 的計(jì)算中出現(xiàn)的表達(dá)式非常相似，其中串聯(lián)臂電抗為?，格臂電抗為?。我們發(fā)現(xiàn)

譯注：式(6a)和(6b)推導(dǎo)如下，依據(jù)格型網(wǎng)絡(luò)傳遞函數(shù)公式：

令且代入上式得到：

求其幅度值：

和式(6)結(jié)果一致。這個(gè)結(jié)果表現(xiàn)出兩格型網(wǎng)絡(luò)分相的相位變化和單個(gè)格型網(wǎng)絡(luò)的幅頻響應(yīng)有類似性。這里作者非常巧妙的由相頻曲線直接類比到了幅頻。

注//en.wikipedia.org/wiki/Lattice_network

通過(guò)比較（6b）和（2），可以看出? 和? 分別從電抗? 和? 中以相同的方式形成。這種相似性對(duì)于分析和綜合分相網(wǎng)絡(luò)具有重要意義，并將在后續(xù)討論中使用。

III. 網(wǎng)絡(luò)分析

本節(jié)的目標(biāo)是為網(wǎng)絡(luò)設(shè)計(jì)和綜合找到函數(shù)? 的一般特性，作為必要的準(zhǔn)備，該函數(shù)由式(2)定義，如果? 是從物理可綜合網(wǎng)絡(luò)得到。由于

我們從? 和? 的特性討論開始。從式(1)中可以得出，作為歸一化頻率? 的函數(shù)， 和? 必須滿足 Foster 的電抗定理；例如，它們必須是? 的奇有理函數(shù)；所有的極點(diǎn)和零點(diǎn)都是簡(jiǎn)單的，并且出現(xiàn)在實(shí)頻率上；零點(diǎn)和極點(diǎn)是交替的；在? 和? 時(shí)，只允許0或這兩個(gè)值。每個(gè)表達(dá)式的分母和分子的次數(shù)差1。

是一個(gè)限制較少的函數(shù)。像? 和? 一樣，它是? 的奇有理函數(shù)，在零和無(wú)窮頻率時(shí)為零或無(wú)窮。但是它的零點(diǎn)和極點(diǎn)不需要交替或出現(xiàn)在實(shí)頻率上，分母和分子的次數(shù)可以相差很大。

這直接來(lái)自于式(7)，并且由于式(6b)，對(duì)于? 和? 同樣有效。現(xiàn)在只處理?，因?yàn)橐? 在從 到? 的帶寬上近似等于1，顯然不允許在這個(gè)帶寬內(nèi)有? 的任何極點(diǎn)或零點(diǎn)。另一方面，我們已經(jīng)看到在? 和? 時(shí)， 將是0或，因此? 將傾向于對(duì)于非常大和非常小的? 值偏離1。因此，建議（參見，例如，Hodgson? ），除了0和，實(shí)? 值不應(yīng)出現(xiàn)任何極點(diǎn)或零點(diǎn)，因?yàn)檫@樣的極點(diǎn)或零點(diǎn)會(huì)增加? 從1的偏離；0和 處的極點(diǎn)或零點(diǎn)應(yīng)為1次。然后，分子和分母的次數(shù)必須相差1。我們將在下一節(jié)中看到，泰勒和切比雪夫逼近將滿足符合此約束的表達(dá)式。

在接下來(lái)的內(nèi)容中，我們將假設(shè)在? 時(shí)，我們有?。然后? 將呈現(xiàn)以下形式

其中? 或 1 ，并且常數(shù)? 和? 以及? 都是正實(shí)數(shù)。我們將用? 表示在? 中出現(xiàn)的? 的最高次冪，并且我們將在后面看到，逼近階數(shù)也可以用? 表示。式（8a）也可以寫成以下形式

其中所有的? 和? 都是實(shí)數(shù)。當(dāng)? 作為? 的函數(shù)關(guān)于?(即?)是對(duì)稱時(shí)，出現(xiàn)了一個(gè)重要的情況，如果? 是奇數(shù)，變換? 導(dǎo)致?；但是如果? 是偶數(shù)，它將保持? 不變。下面列出了當(dāng)? 是對(duì)稱且?值從 1 到 6 時(shí)的? 的表達(dá)式：

以上公式為分析網(wǎng)絡(luò)提供了基本的框架，并為接下來(lái)的網(wǎng)絡(luò)設(shè)計(jì)和綜合奠定了基礎(chǔ)。通過(guò)這些公式，我們可以更好地理解分相網(wǎng)絡(luò)的基本特性和參數(shù)，為進(jìn)一步的研究和分析提供了重要的參考。

譯注：上面的式8(c)實(shí)際上是對(duì)擬合的波形做了一個(gè)約束：

是一個(gè)有理多項(xiàng)式的比(可實(shí)現(xiàn)性)

當(dāng)時(shí)，(可實(shí)現(xiàn)性)

當(dāng)時(shí)，(濾波器的通帶部分，保證相位90°的條件)

當(dāng)為奇數(shù)時(shí)，當(dāng)時(shí)，函數(shù)(關(guān)于(1,1)中心對(duì)稱)

當(dāng)為偶數(shù)時(shí)，當(dāng)時(shí)，函數(shù)(關(guān)于軸對(duì)稱)

通過(guò)以上約束條件可以求出式(8c)，這里以舉例說(shuō)明：

由式(8a)可知

令得到：

上面兩式相等得到：

這樣得到式(8c)的表達(dá)式。

IV. 所需性能曲線的逼近

在本節(jié)中，我們將討論尋找使得?, 或? 在范圍? 到? 內(nèi)成為逼近1的最佳近似的常數(shù)值的方法。如果需要的其他值，比如，那么在接下來(lái)的討論中，必須替換為。我們將從泰勒(Taylor)和切比雪夫(Tchebycheff)近似開始，因?yàn)樵谶@里可以超越逼近方法的推薦，給出明確的公式，這些公式可以根據(jù)?（即? 的范圍）給出常數(shù)。

在本節(jié)中，我們將討論在表達(dá)式，或中尋找這些待定常數(shù)值的方法，使得在從到的范圍內(nèi)成為對(duì)1的良好近似。如果需要的其他值，比如，則在接下來(lái)的討論中，必須替換為。在討論泰勒和切比雪夫近似時(shí)，我們不僅可以推薦這些方法，更能進(jìn)一步得出具體的公式來(lái)明確表達(dá)常數(shù)，這些公式用表示常數(shù)，如用的范圍表示常數(shù)。

1. 泰勒逼近

第階的泰勒逼近的特點(diǎn)是存在個(gè)設(shè)計(jì)參數(shù)，它們被選擇成這樣的值，以便對(duì)于指定的值，比如說(shuō)，本身和前個(gè)微分系數(shù)，對(duì)于，對(duì)于所需曲線和逼近曲線是相同的。因此，越高，逼近曲線越接近所需曲線。

如果我們假設(shè)，那么第階的泰勒逼近由下式給出：

通過(guò)將式(9a)寫成下面的形式：

譯注：這里突然冒出來(lái)的(9a)公式實(shí)在是沒有理解，查閱相關(guān)資料得到：

可以看到這個(gè)和切比雪夫多項(xiàng)式非常類似，有人對(duì)其進(jìn)行了推導(dǎo)：

這個(gè)公式在處對(duì)y=1進(jìn)行了非常好的逼近，如下圖(4a)給出了的函數(shù)圖像。

我們看到在中出現(xiàn)的的最高次數(shù)是，并且是關(guān)于對(duì)數(shù)頻率刻度對(duì)稱的奇有理函數(shù)。

將其寫成如下形式：

我們可以很容易地證明（令 和? ），在處的前個(gè)微分系數(shù)為零，這符合對(duì)的泰勒逼近的要求。下面列出的的表達(dá)式：

這些曲線在圖4(a)中用對(duì)數(shù)-對(duì)數(shù)坐標(biāo)繪制，

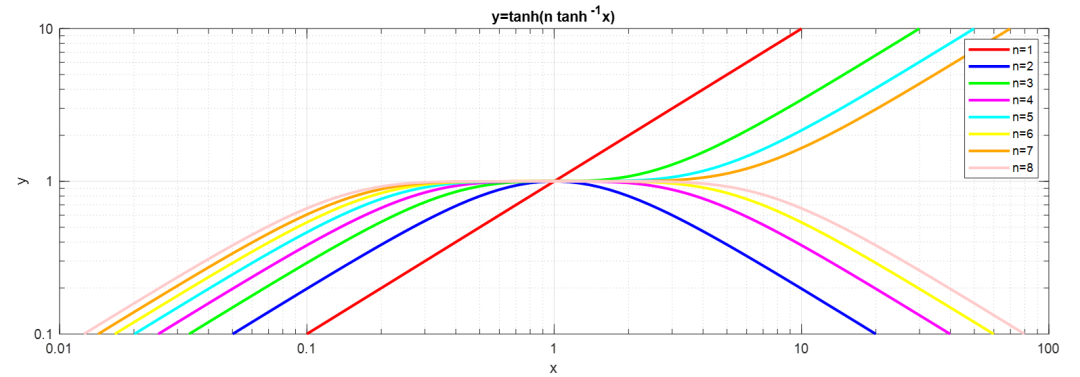
圖 4(a) 泰勒逼近

對(duì)于范圍從到，即對(duì)于。例如，這對(duì)應(yīng)于頻率范圍從到。

從(9b)中可以看出，如果被替換，對(duì)于偶數(shù)值保持不變，并且對(duì)于奇數(shù)值被替換。與的偏差隨著的增加而增加。如果范圍的限制表示為和，并且范圍的限制表示為和，則作為的函數(shù)由下式給出：

就函數(shù)關(guān)系而言，這與(9a)相似。如果我們以下面的形式寫出(9e)：

我們可以看到，如果我們?yōu)楹褪褂糜珊瘮?shù)定義的刻度，那么作為的函數(shù)可以表示為通過(guò)坐標(biāo)系原點(diǎn)的直線，對(duì)于任何值，斜率為。這已在圖4(b)中示出來(lái)。

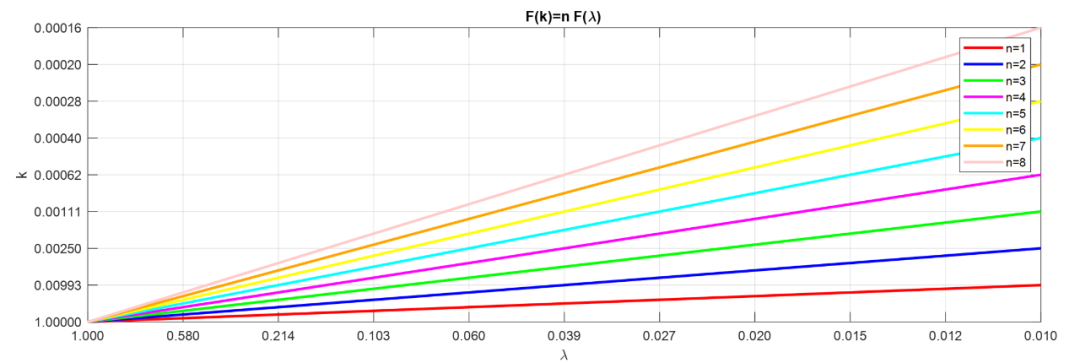
圖 4(b) 泰勒逼近與所需性能的偏差

考慮到(9f)和(9a)之間的功能相似性，圖4(b)也表示作為的函數(shù)，換句話說(shuō)，圖4(b)可以看作顯示與圖4(a)相同的曲線。可以看到，如果是給定的，那么隨著的增加而減小，即的范圍變得更小。

為了綜合具有由式(9a)所描述性能的網(wǎng)絡(luò)，我們必須找到（如將在第V節(jié)中解釋的）時(shí)的值。它們由下式給出：

2. 切比雪夫逼近

切比雪夫逼近的特點(diǎn)是出現(xiàn)的最大偏差是最小的。橢圓函數(shù)的變換理論非常方便地描述了關(guān)于的對(duì)數(shù)-軸對(duì)稱的關(guān)于的奇有理函數(shù)，在范圍到內(nèi)，以切比雪夫的方式逼近，值在范圍和內(nèi)。如上所述，的這些限制等效于相位差的偏差從所需值的最大和最小偏差和，以及。使用Cayley的符號(hào)，可以很容易地證明階的切比雪夫逼近由下式給出：

在由(10a)和(10b)定義的有理函數(shù)中出現(xiàn)的的最高次數(shù)是。Cayley用后綴'1'表示和，以表示從模數(shù)到較大的模數(shù)的"第二變換"。然而，在接下來(lái)的討論中，很多情況下使用后綴來(lái)表示變換的順序是方便的。因此，為了避免混淆，將不使用Cayley的后綴'1'。為了本討論的目的，有時(shí)也方便地表示為。在式(10a)和(10b)中，是由(10b)定義的輔助變量，而是由(10a)通過(guò)定義的。已在上面定義過(guò)。可以從得出和如下：是的函數(shù)，比如說(shuō)是橢圓函數(shù)理論中已知的（例如由Hayashi1編制的表格表示的函數(shù)，即。可以通過(guò)下面的關(guān)系從獲得：

接下來(lái)，如果給定，隨著的增加，會(huì)減小，即的范圍變得更小。此外，可以在Hayashi的表中找到作為的函數(shù)，以及作為的函數(shù)。然后由下式給出：

譯注:這里使用的雅克比橢圓函數(shù)與一般的橢圓函數(shù)濾波器所使用的方法不同，這里利用了橢圓函數(shù)的雙周期特性，讓橢圓函數(shù)往虛軸方向平行擺放對(duì)齊，再使用虛軸一側(cè)實(shí)現(xiàn)等紋波特性。可以將公式寫為更為緊湊的形式：

下圖式時(shí)平面零極點(diǎn)分布圖：

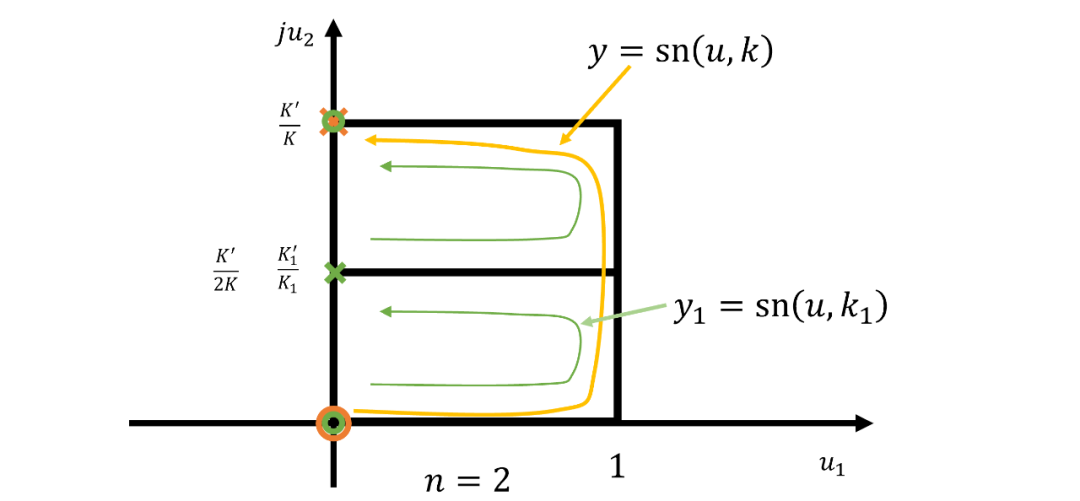
表 Ia切比雪夫逼近法；和作為的函數(shù)。

下表和圖顯示了作為以的函數(shù)的情況：

比(10b)更好的一個(gè)形式：

給出作為的函數(shù)的最佳表達(dá)式，如果

因此，可以為任何和得到，并且，當(dāng)被指定時(shí)，可以選擇以使（表示從0的最大偏差）盡可能小。作為和的函數(shù)在圖5(b)中表示。由于(10c)的形式與(9f)相同，因此如果對(duì)和使用線性刻度，再次可以將曲線繪制為斜率為的直線。應(yīng)該注意，在切比雪夫逼近的情況下，關(guān)聯(lián)到的曲線（圖5b）并不同時(shí)關(guān)聯(lián)到。可以看出，對(duì)于任何給定的和值，從圖5(b)獲得的值，即對(duì)于切比雪夫逼近法，比從圖4(b)獲得的值，即對(duì)于泰勒逼近法，更接近1。

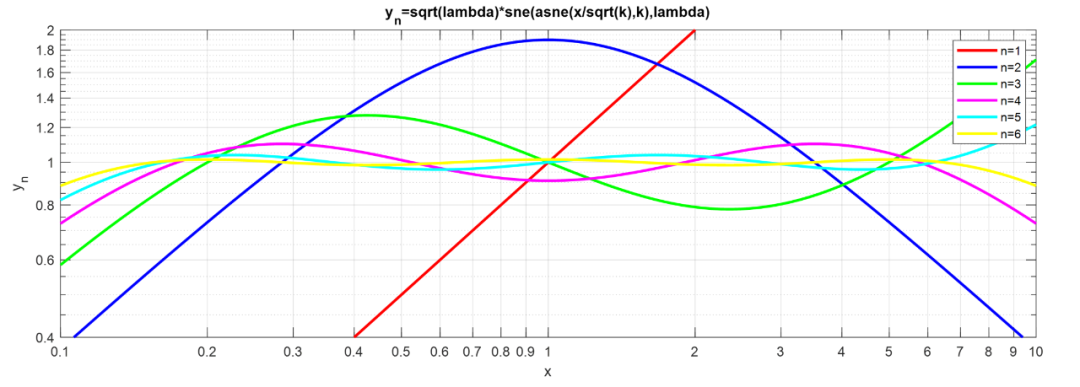
圖 5(a) 切比雪夫逼近法。

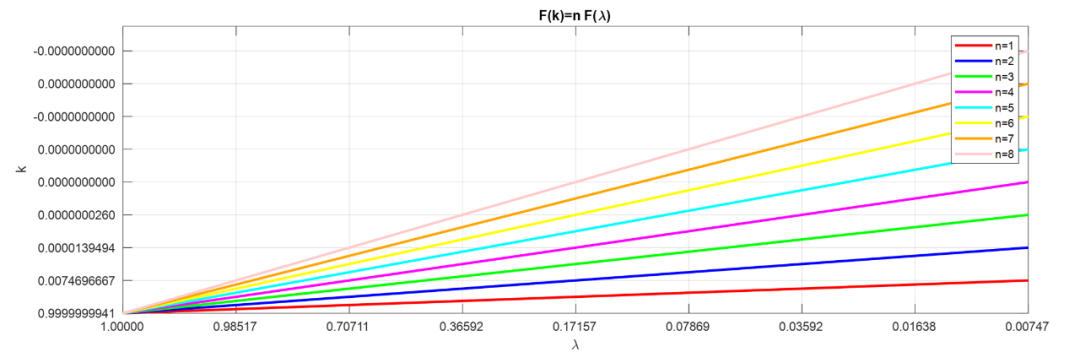
圖 5(b) 切比雪夫逼近法與所需性能的偏差。

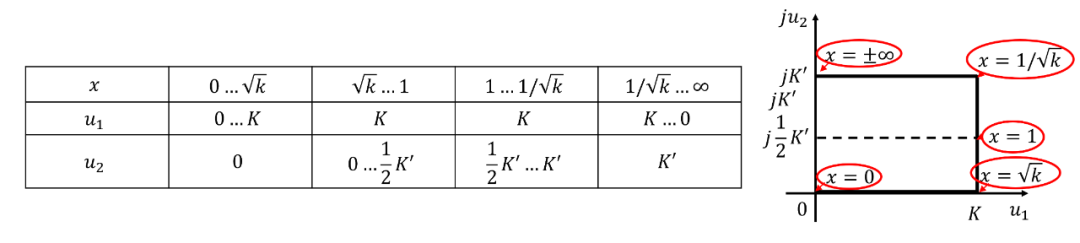
作為的函數(shù)可以通過(guò)橢圓函數(shù)的表格直接從(10a)和(10b)中評(píng)估，例如，Milne-Thomson的表格和Hayashi的表格。為此，式(10a)和(10b)可以按照表I(a)中顯示的方式進(jìn)行修改。圖5(a)示意性地顯示了的切比雪夫逼近，其中的范圍從到，其中。對(duì)于這些圖表，沒有使用表中給出的公式。僅評(píng)估了出現(xiàn)最大值或最小值的值以及的值，并且已經(jīng)畫出了通過(guò)這些點(diǎn)的曲線。然而，對(duì)于（見第VI節(jié)），大量點(diǎn)的數(shù)值檢查顯示了與繪制的曲線非常好的一致性。曲線呈振蕩行為，所有的最大值和最小值分別發(fā)生在值和處，的值取決于所考慮的值和值。對(duì)于偶數(shù)值，有個(gè)最大值，個(gè)最小值，兩個(gè)與線的交點(diǎn)和個(gè)與線的交點(diǎn)。對(duì)于奇數(shù)值，有個(gè)最小值和個(gè)最大值，一個(gè)與線的交點(diǎn)，一個(gè)與線的交點(diǎn)和個(gè)與線的交點(diǎn)。

為了能夠繪制的這些特征點(diǎn)，我們必須知道和時(shí)的值。另一方面，為了能夠以式(8c)的形式將寫為的有理函數(shù)，我們必須知道和時(shí)的值，以及在偶數(shù)值的情況下的值（見下文）。最后，為了綜合一個(gè)根據(jù)的性能曲線的網(wǎng)絡(luò)，我們必須找到時(shí)的值。所有這些的值可以通過(guò)首先反轉(zhuǎn)(10a)來(lái)找到作為的函數(shù)，然后將的這個(gè)表達(dá)式代入(10b)中得到。然而，為了簡(jiǎn)化切比雪夫逼近法的工程應(yīng)用，列出了變?yōu)?? 和?時(shí)的值，分別在表I，II和III中。列表中的表達(dá)式形式規(guī)則，如果需要，很容易通過(guò)類推將表格擴(kuò)展到任何值。上文提到的值由下式給出：

表 Ib切比雪夫逼近； 作為? 的函數(shù)。

令?，則

?

?

此表在表II和III中有更詳細(xì)的說(shuō)明。

在處理切比雪夫逼近時(shí)，通常很方便使用對(duì)這些逼近有效的“指數(shù)定律”。令? 表示在范圍? 到?上對(duì)? 的第階逼近，并且讓? 表示? 的變化范圍，即， 在? 和? 之間變化。此外，讓? 表示在? 范圍? 到? 上對(duì)? 的第階逼近，并且讓? 表示? 的變化范圍，即， 在? 和? 之間變化。那么，當(dāng)從變化到時(shí)，將視為的函數(shù)與范圍到上對(duì)的第階逼近是相同的，如果。這可以通過(guò)以下公式表示：

憑借指數(shù)定律，如果我們已經(jīng)探討了的情況，我們可以將所有獲得的結(jié)果應(yīng)用于? 和?。如果我們已經(jīng)探討了和，我們可以結(jié)合結(jié)果以獲得 和?的情況。指數(shù)定律的一般化解釋將在附錄中給出。

表 II

切比雪夫逼近；對(duì)于的。

?

?

表 III

切比雪夫逼近；對(duì)于的。

?

?

3. 切比雪夫逼近的替代理論

到目前為止，我們已經(jīng)使用橢圓函數(shù)討論了切比雪夫逼近的理論。這導(dǎo)致了最簡(jiǎn)潔和最通用類型的表達(dá)式。同時(shí)，必須認(rèn)識(shí)到許多工程師不熟悉橢圓函數(shù)，并且有時(shí)很難獲得良好的橢圓函數(shù)表。因此，重要的是要注意，有可能純粹代數(shù)地制定逼近法，而無(wú)需使用橢圓函數(shù)。在實(shí)踐中，結(jié)合兩種方法，適用于正在考慮的特定案例，有時(shí)是最佳選擇。對(duì)于，代數(shù)理論實(shí)際上非常簡(jiǎn)單。從開始，可推出以下關(guān)系：

對(duì)于和；

對(duì)于。

條件得到和。對(duì)于的這個(gè)值，是范圍的第二階切比雪夫逼近。可以通過(guò)應(yīng)用指數(shù)定律來(lái)討論和的情況。結(jié)果列在表IV中。

表 IV

對(duì)于? 的切比雪夫逼近; 代數(shù)關(guān)系

?

?

對(duì)于?，推導(dǎo)? 的表達(dá)式?jīng)]那么簡(jiǎn)單。我們從形式為? 的表達(dá)式開始，為了使其關(guān)于? 對(duì)稱，簡(jiǎn)化為?。接著我們需要確定? 的值，以便在給定的范圍? 內(nèi)， 以切比雪夫方式呈現(xiàn)。要求當(dāng)? 時(shí)， 等于?；此外，在未知的? 值，比如說(shuō)? 處， 的值也應(yīng)為? 的最小值。因此

必須等于?。比較系數(shù)，我們得到三個(gè)方程：

如果我們引入?(由Cayley提出的術(shù)語(yǔ))

我們發(fā)現(xiàn)

和

式(13a) 和 (13b) 以? 的形式確定了? 和? （ 也可以通過(guò)橢圓函數(shù)的表格或像圖 5(b) 中的圖表來(lái)確定）。接著我們可以找到?。因此我們知道? 是? 的函數(shù)以及以下的細(xì)節(jié)：

如果我們?cè)谟懻? 的情況時(shí)，將獨(dú)立變量? 替換為二階逼近?，并將? 替換為?，我們將得到六階逼近，并通過(guò)重復(fù)這個(gè)過(guò)程，我們可以得到十二階逼近。如果在討論? 的情況時(shí)，我們將? 替換為?，并將? 替換為?，我們將得到九階逼近。然而，對(duì)于質(zhì)數(shù)? 等，代數(shù)理論變得逐漸困難（參見 Cayley）。

譯注：前述的代數(shù)計(jì)算方法類似暴力計(jì)算，基本思想是函數(shù)曲線關(guān)于1對(duì)稱且等紋波起伏，然后利用對(duì)稱性計(jì)算其他相關(guān)階數(shù)的表達(dá)式。

4. 通過(guò)其他方法逼近

在大多數(shù)情況下，關(guān)于分相網(wǎng)絡(luò)性能的要求可能可以通過(guò)前一節(jié)討論的切比雪夫或泰勒逼近來(lái)滿足。然而，有時(shí)可能會(huì)一些額外的設(shè)計(jì)約束，對(duì)于這些約束，這些類型的逼近并非最佳可能的解決方案。然后需要一些其他類型的逼近。

如果要求在的個(gè)特定值處具有精確的相位差，則可以通過(guò)解? 個(gè)線性方程組來(lái)獲得滿足這些要求的函數(shù)? 的參數(shù)。Zobel? 已經(jīng)詳細(xì)討論了這種方法，參考了衰減均衡器和相移網(wǎng)絡(luò)的設(shè)計(jì)。應(yīng)用于分相網(wǎng)絡(luò)的設(shè)計(jì)不會(huì)有任何新的問題。

Zobel 建議不僅在指定了多個(gè)點(diǎn)的性能的情況下使用這種方法，而且在需要對(duì)整個(gè)? 值范圍進(jìn)行良好逼近的情況下也使用這種方法。然而，在這種情況下，Zobel 的方法通常會(huì)導(dǎo)致失望的結(jié)果（參見例如 Saraga? 和 Baum? 的評(píng)論），而且更傾向于使用圖像進(jìn)行曲線擬合的方法。

對(duì)圖形曲線擬合方法的研究顯示，它們可以方便地分類為曲線求和或曲線移位和成形方法(curve shifting and shaping methods)（參見 Saraga?）。通常需要轉(zhuǎn)換指定所需性能曲線及其容差帶的坐標(biāo)系，以便可能應(yīng)用這些圖形方法。在求和方法中，通過(guò)在不同位置添加多條標(biāo)準(zhǔn)曲線獲得符合容差帶的曲線。從這些位置可以獲得逼近曲線的參數(shù)（例如，參見 Laurent, Rumpelt,? Saraga,? Scowen,? Baum?）。在移位和成形方法中，只能用于有限數(shù)量（不超過(guò) 4 到 5）的參數(shù)，通過(guò)比例變化和剪切移動(dòng)和成形一個(gè)單一的標(biāo)準(zhǔn)曲線，直到它符合所需的容差帶（參見 Pyrah,? Truscott,? Saraga?）。我們不在這里討論這些方法應(yīng)用于分相網(wǎng)絡(luò)的特定問題。

V. 網(wǎng)絡(luò)綜合

在這一節(jié)，我們假設(shè)已經(jīng)以某種方式確定了合適的性能函數(shù)。下一步是確定兩個(gè)相移網(wǎng)絡(luò)，這些網(wǎng)絡(luò)將產(chǎn)生這個(gè)函數(shù)。要解決的問題是當(dāng)

已知時(shí)，找到和。由于在對(duì)稱濾波器的設(shè)計(jì)中也出現(xiàn)了這個(gè)問題（見公式（6b））

給出和，并且必須找到物理上可實(shí)現(xiàn)的電抗，我們可以將其解應(yīng)用于我們的問題。Darlington?給出了確定電抗的以下指導(dǎo)（在此根據(jù)本文中使用的符號(hào)進(jìn)行了修改）：將寫成的形式，其中和是的多項(xiàng)式。然后將表示為的形式，其中是的偶次多項(xiàng)式，使得的根（即）具有負(fù)實(shí)部。那么和。

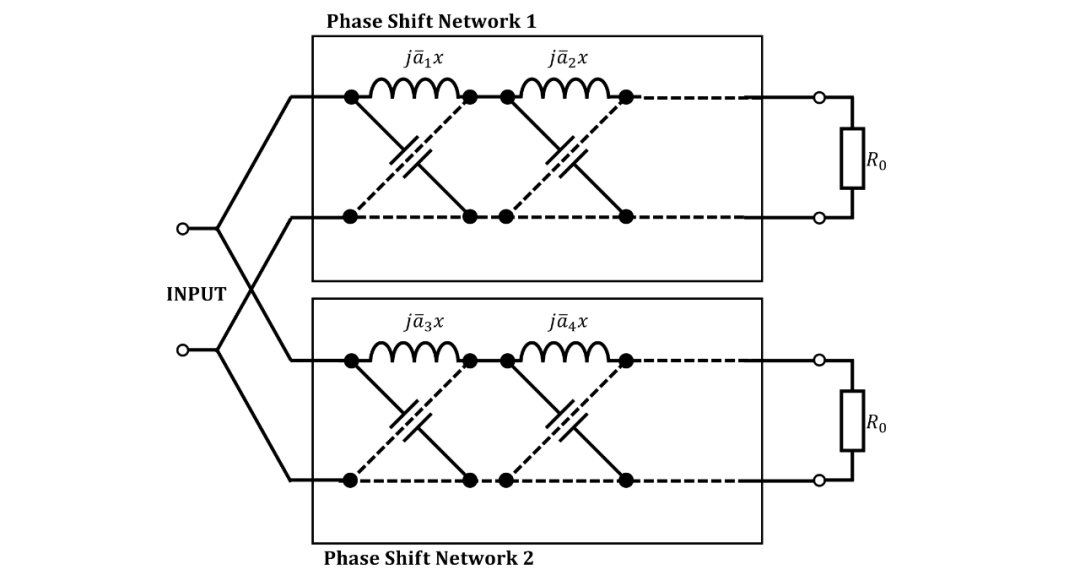
圖 6. 基本分相電路，分解成基本相移段。

Darlington 的方法，雖然沒有明確的證明，但可以以包括證明的方式進(jìn)行修改。為此，我們考慮在? 的? 值；在這些值，比如說(shuō)?，相位差? 接近?，這必須是由于? 趨向于? 或? 趨向于?。現(xiàn)在假設(shè)兩個(gè)基本相移網(wǎng)絡(luò)具有串聯(lián)電抗? 和?（參見圖 1），由串聯(lián)的“基本”相移段組成，每個(gè)段的特征是其相移? 和其歸一化的串聯(lián)臂電抗? 或其歸一化的串聯(lián)臂電感?（參見圖 6）。 然后在每個(gè)? 處，這些基本相位角之一? 必須趨向于?，并且?，如果? 是? 的組成部分，或趨向于? 并且?，如果? 是? 的組成部分。由于?，我們發(fā)現(xiàn)?。我們選擇使?，歸一化的電感，為正的符號(hào)。如果為了獲得正的?，我們必須采取正符號(hào)，則相應(yīng)的? 是? 的組成部分，而在另一種情況下，我們得到了? 的組成部分。通過(guò)這種方式，我們不僅找到了? 和?，而且同時(shí)也找到了組成兩個(gè)基本相移網(wǎng)絡(luò)的基本段。可以證明，根據(jù)正切函數(shù)的加法定理，從基本相移段的電感中形成? 和? 的表達(dá)式會(huì)導(dǎo)出由 Darlington 給出的表達(dá)式。

將看到， 個(gè)基本段導(dǎo)致? 中? 的最高次數(shù)為?，反之亦然。因此，網(wǎng)絡(luò)元件的數(shù)量隨著? 的最高次數(shù)的增加而增加。

譯注：上面給出了綜合的基本方法，其基本方法是找傳遞函數(shù)的"特征值"上，即極點(diǎn)，這些極點(diǎn)剛好是的解，而一個(gè)對(duì)稱格型網(wǎng)絡(luò)電路中又有，在橢圓函數(shù)中也可以很方便的求出極點(diǎn)，所以，通過(guò)極點(diǎn)將相位和器件值所關(guān)聯(lián)，從而可以綜合出所需電路。

VI. 兩個(gè)實(shí)用設(shè)計(jì)示例

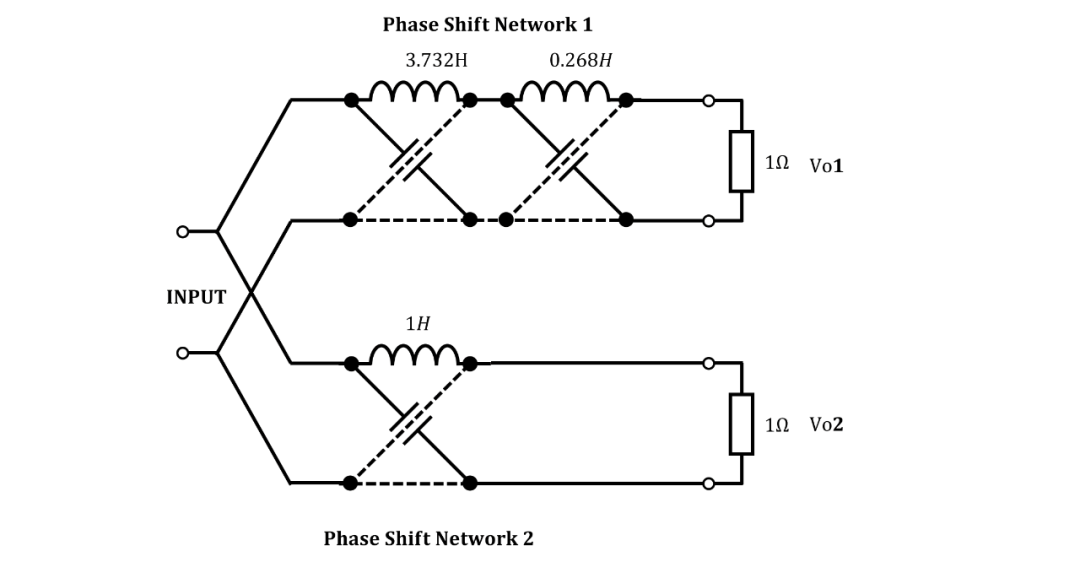
選擇實(shí)際示例以供本文討論時(shí)，最好選擇非常簡(jiǎn)單的示例，因?yàn)檫@樣可以最清楚地展示獲得網(wǎng)絡(luò)的方法。首先，我們將討論一個(gè)需要泰勒近似的案例，我們選擇一個(gè)簡(jiǎn)單的案例，即?。然后，最佳逼近由

給出（參見式（9d））。由于? 是奇數(shù)，兩個(gè)相移網(wǎng)絡(luò)的段數(shù)必須相差1。假設(shè)帶有? 的網(wǎng)絡(luò)由兩個(gè)段組成，分別具有串聯(lián)臂電感? 和?。那么具有? 的網(wǎng)絡(luò)有一個(gè)單獨(dú)的段，例如帶有串聯(lián)臂電感?。因此我們得到

和

在這種簡(jiǎn)單情況下，我們可以通過(guò)比較（14）和（15）中的系數(shù)來(lái)獲得?。那么?；

代入計(jì)算，我們得到了一個(gè)關(guān)于? 的三次方程，其中一個(gè)正根是：。然后?，并且? 和? 可以互換。在更復(fù)雜的情況下，我們將解方程?，并通過(guò)方程? 或代數(shù)方法得到三個(gè)根? 和?。根據(jù)根的符號(hào)，第一個(gè)必須對(duì)應(yīng)于?，其他兩個(gè)必須對(duì)應(yīng)于?。因此，我們像前述一樣得到? 和?。

譯注：上述綜合原理圖如下：

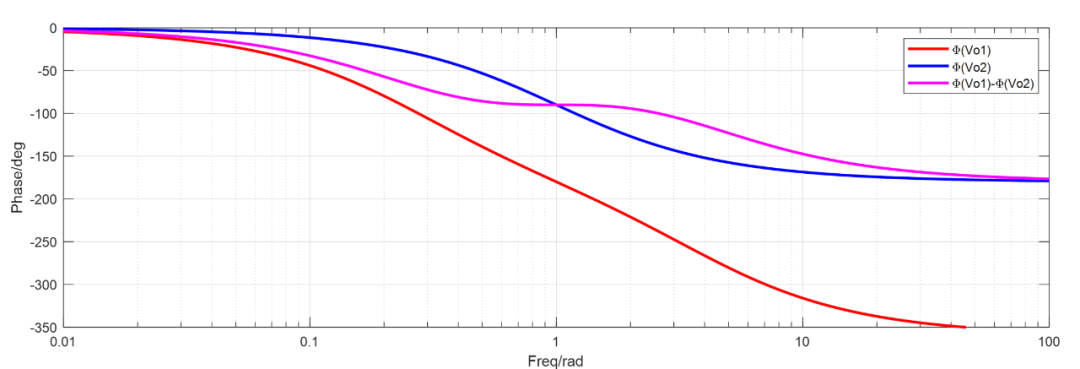
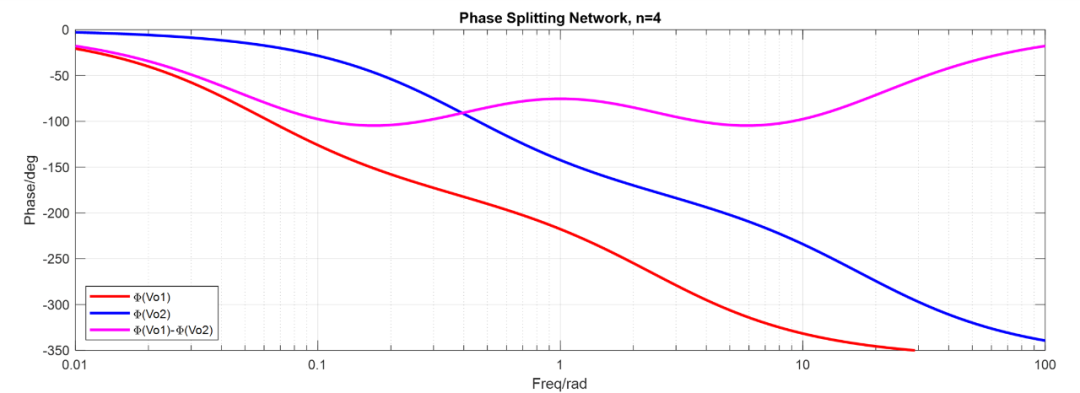
仿真得到和的輸出相頻以及相頻差圖如下：

作為第二個(gè)示例，我們將討論一個(gè)需要 Tchebycheff 逼近的示例。我們將取?，以便我們可以使用代數(shù)方法以及橢圓函數(shù)的變換來(lái)獲得網(wǎng)絡(luò)元件。指定的? 范圍假定為從? 到?，其中?。這對(duì)應(yīng)于頻率范圍從? 到?。然后通過(guò) Hayashi 的表格，找到? 為 0.5959。 曲線顯示在圖 5（a）中。表 II 給出了? 時(shí)四個(gè)? 值的表達(dá)式。然后使用 Milne-Thomson 的表格，我們找到?,?。然后對(duì)于一個(gè)相移網(wǎng)絡(luò)? 和對(duì)于另一個(gè)網(wǎng)絡(luò)?。從? 的這些值中，我們發(fā)現(xiàn)

和? 和? 可以互換。

應(yīng)用代數(shù)理論，我們從表 IV 中得到

和

與之前相同。

譯注：這里通過(guò)值查表的過(guò)程可以很方便的使用matlab函數(shù)實(shí)現(xiàn)(實(shí)際上就是找到滿足兩個(gè)橢圓函數(shù)在平面對(duì)齊的條件)：

?

?

n = 4;
k = 0.003;
lambda = ellipdeg(n, k);

>> 
lambda = 0.5959

?

?

求解的值使用matlab也非常方便：

?

?

[K,Kp]   = ellipk(k);
a_bar    = zeros(1, n);
for ii=1:n
    a_bar(ii) = sqrt(k)*sne(1i*(1+4*(ii-1))/(2*n)*Kp/K, k);
    fprintf('a_bar(%d) = %0.5f j
', ii, imag(a_bar(ii)));
end

>>
a_bar(1) =   0.05618 j
a_bar(2) =   2.46908 j
a_bar(3) = -17.79989 j
a_bar(4) =  -0.40501 j

?

?

綜合得到的電路如下：

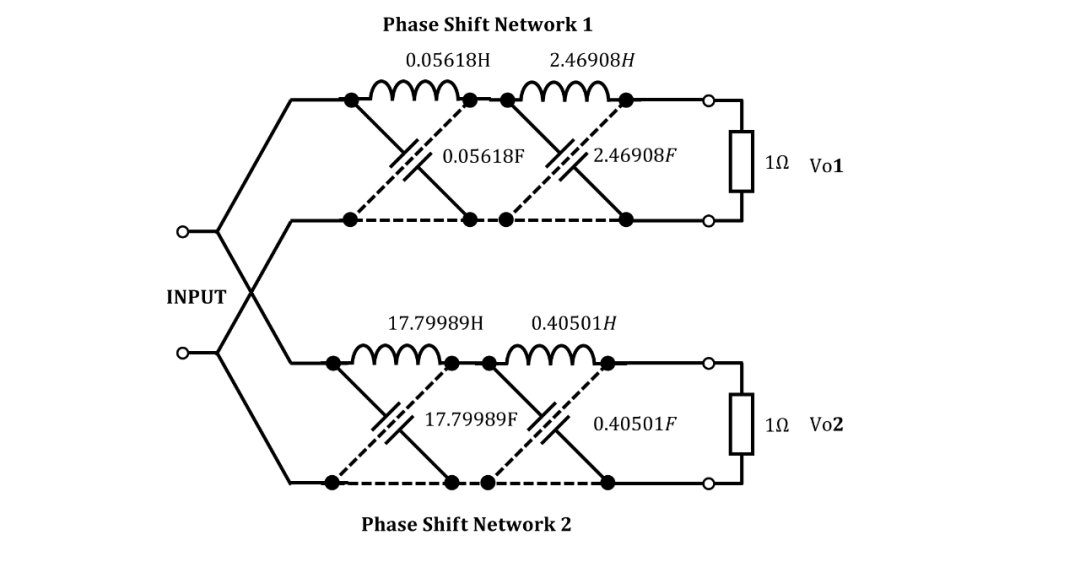
仿真波形如下：

VII. 相移網(wǎng)絡(luò)的替代

前面的討論基于傳統(tǒng)的恒定阻抗相移網(wǎng)絡(luò)，其串聯(lián)臂電抗為? 和格臂電抗為?，插入在等值電阻? 之間。然后相移為?。可以在不改變相移的情況下改變其中一個(gè)電阻；然后會(huì)產(chǎn)生固定的平坦插損。這在圖7中示出。

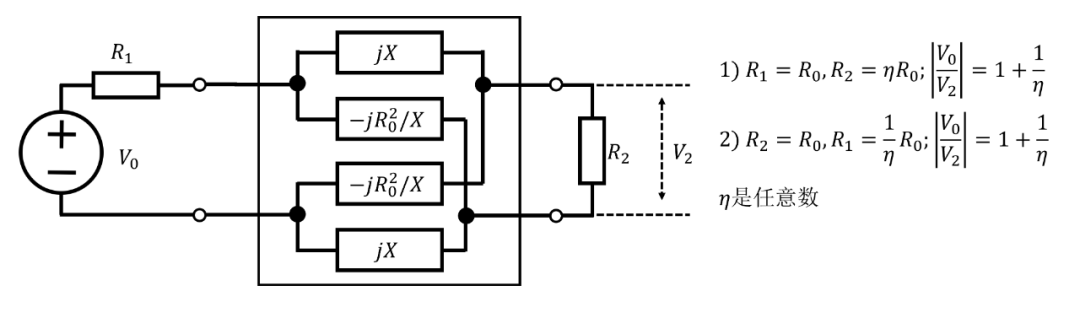
圖 7. 經(jīng)典相移格型網(wǎng)絡(luò)

Marrison? 已經(jīng)證明，可以用電阻替換兩個(gè)格臂電抗，而不改變相移（見圖8）。

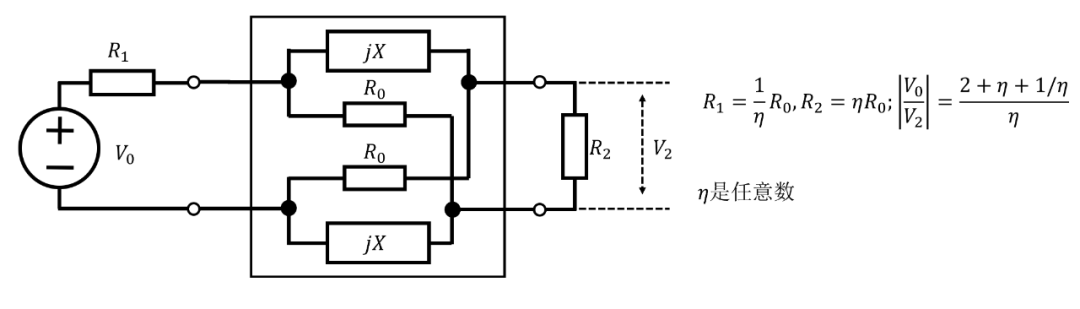
圖 8. 圖 7 網(wǎng)絡(luò)的替代方案

然后，如果源阻抗和負(fù)載電阻都等于，則產(chǎn)生平坦的插損。可以使源電阻為，負(fù)載電阻為。然后產(chǎn)生了取決于的附加平坦插損，但相移仍然不變。Saraga?已經(jīng)證明，可以用電阻替換剩下的兩個(gè)電抗臂中的一個(gè)（見圖9），而不改變相移。

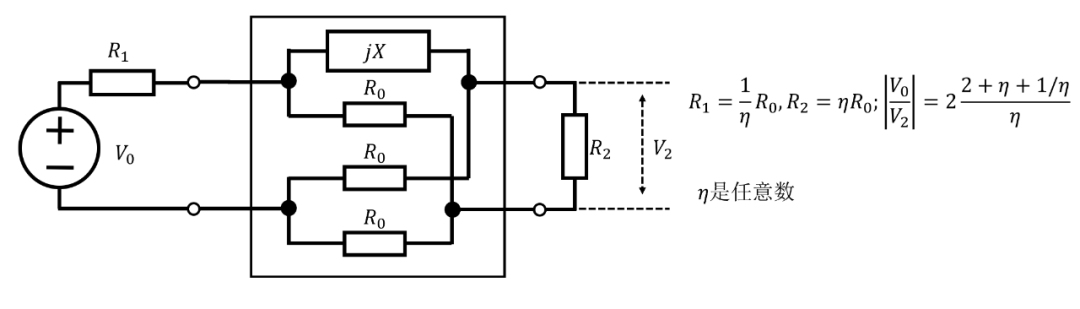
圖 9. 圖 7 網(wǎng)絡(luò)的替代方案

然后，如果，固定插損是而不是。兩種其他類型的相移網(wǎng)絡(luò)，一種是Nyquist型，由Sandeman?描述（見圖10），

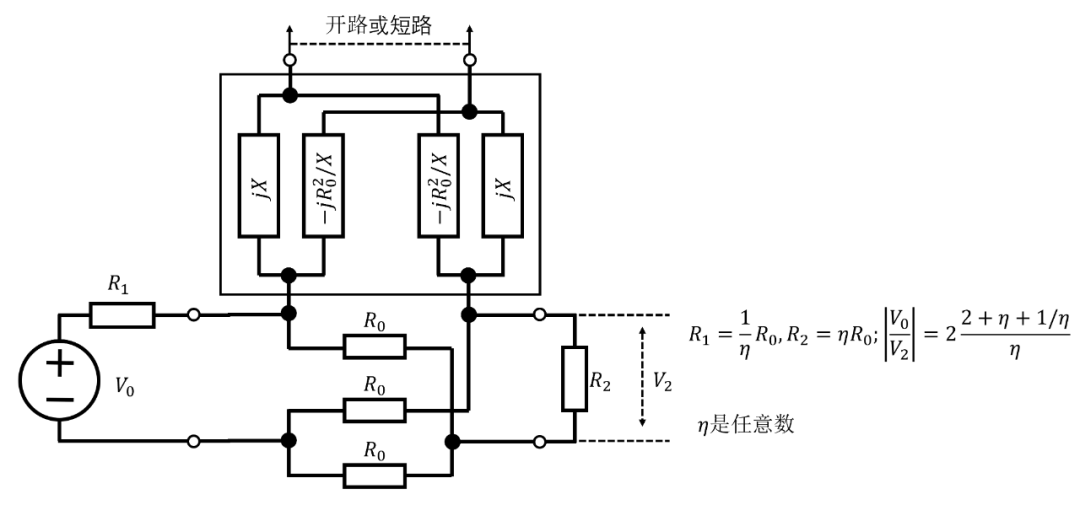
圖 10. 圖 7 網(wǎng)絡(luò)的替代方案

另一種由Wald?描述（見圖11）可以被證明是圖9中網(wǎng)絡(luò)的特殊情況，但是具有比實(shí)際產(chǎn)生相移所需的更多電抗元件。

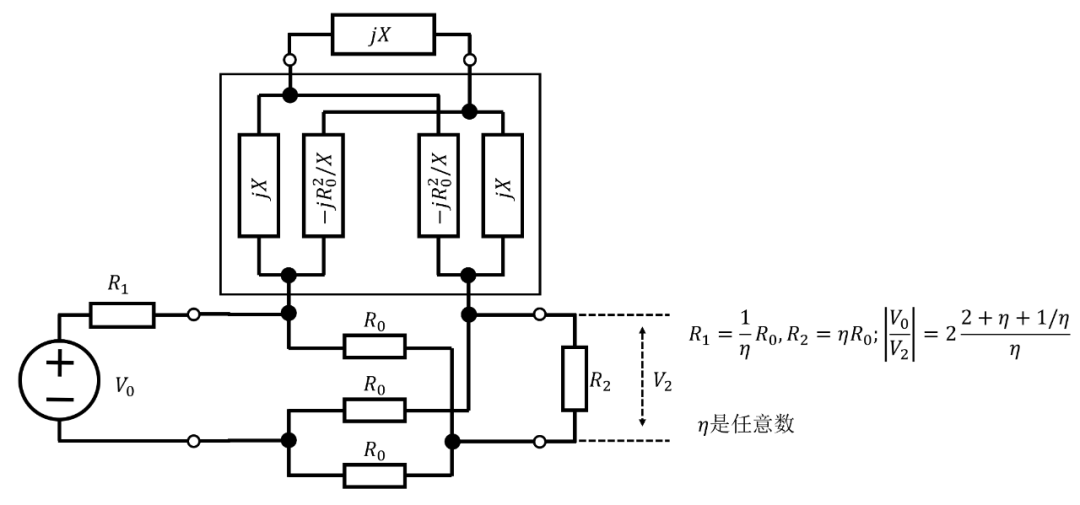
圖 11. 圖 7 網(wǎng)絡(luò)的替代方案

圖9中的電路可以用混合電路替換（見Sandeman）。Dome?和Luck?描述了許多所謂的半格網(wǎng)絡(luò)，這些網(wǎng)絡(luò)由差分源驅(qū)動(dòng)。

VIII. 損耗補(bǔ)償移相網(wǎng)絡(luò)

在移相網(wǎng)絡(luò)的元件中，損耗效應(yīng)會(huì)扭曲相位特性并產(chǎn)生隨頻率變化的衰減。如果不同元件的? 值不同，阻抗也會(huì)受到影響。Starr? 描述了近似補(bǔ)償這些損耗效應(yīng)的方法。Darlington? 和 Bode? 描述了完美補(bǔ)償損耗效應(yīng)的方法。網(wǎng)絡(luò)的設(shè)計(jì)是為了滿足預(yù)失真的指標(biāo)，這些指標(biāo)是通過(guò)假設(shè)負(fù)損耗的發(fā)生從原始指標(biāo)中得到的；然后正損耗產(chǎn)生了所需的性能。這里將描述獲得損耗補(bǔ)償相移網(wǎng)絡(luò)的不同方法。

由于任何相移網(wǎng)絡(luò)都可以作為單、雙參數(shù)相移網(wǎng)絡(luò)的串聯(lián)組合來(lái)構(gòu)建，因此只需考慮這種網(wǎng)絡(luò)的損耗補(bǔ)償就足夠了，該方法的基本思想是僅考慮包含與每個(gè)電感串聯(lián)的電阻和與每個(gè)電容并聯(lián)的電阻的網(wǎng)絡(luò)，以便這些電阻可以承擔(dān)電抗元件的損耗電阻，并設(shè)計(jì)這些網(wǎng)絡(luò)，使它們具有所需的相位特性? 和平坦損耗?。對(duì)于圖 12 中的格型網(wǎng)絡(luò)，傳遞常數(shù)? 由? 給出。

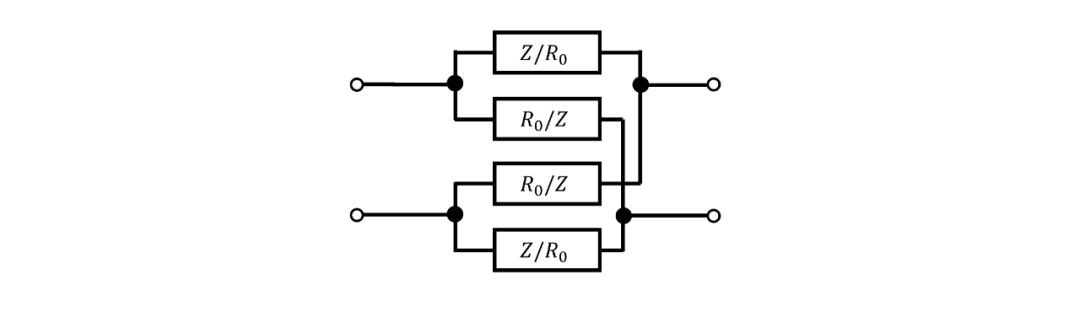
圖 12. 格型網(wǎng)絡(luò)，與圖 13 和圖 14 一起顯示以供參考。

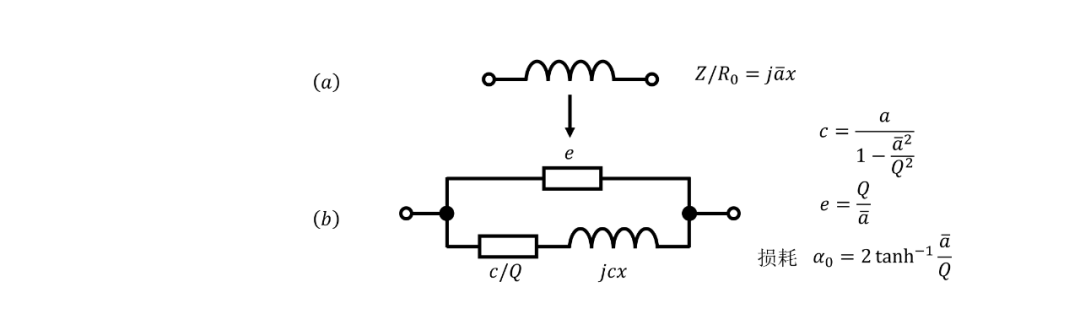
圖 13. 單參數(shù)相移網(wǎng)絡(luò)的損耗補(bǔ)償。

對(duì)于無(wú)損耗的單參數(shù)相移網(wǎng)絡(luò)?（見圖 13(a)），并且?。我們的目標(biāo)是找到一個(gè)阻抗?，其電阻如上所述，使得?，其中?， 是網(wǎng)絡(luò)的基本損耗。可以很容易地證明圖 13(b) 中的網(wǎng)絡(luò)代表了這種形式的阻抗?。如果? 不是太小，它的元件值將是正的。

現(xiàn)在我們考慮雙參數(shù)相移網(wǎng)絡(luò)（無(wú)損耗），其中? 如圖 14(a) 所示。然后

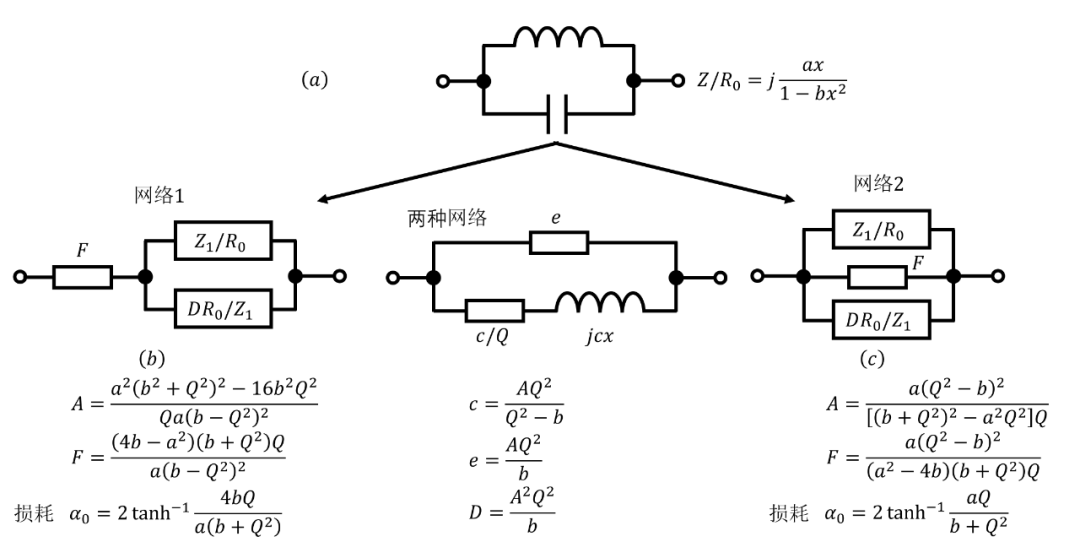
圖 14. 雙參數(shù)相移網(wǎng)絡(luò)的損耗補(bǔ)償。

我們需要找到一個(gè)阻抗?，其電阻如上所述，使得

可以證明，如果滿足圖 14(b) 和 14(c) 中所述的關(guān)系，這兩個(gè)網(wǎng)絡(luò)具有這種阻抗。在圖 14(c) 中，當(dāng)然可以將電阻? 吸收到? 中。可以看到，如果?，則圖 14(b) 中的電阻? 為負(fù)，如果?，則圖 14(c) 中的電阻? 為負(fù)。在圖 14(c) 中， 也可能是物理可實(shí)現(xiàn)網(wǎng)絡(luò)。

如果?，則可以用圖 13(a) 中串聯(lián)阻抗定義的兩個(gè)更簡(jiǎn)單的網(wǎng)絡(luò)替換圖 14(a) 中串聯(lián)臂電抗定義的相移網(wǎng)絡(luò)。如第 V 節(jié)腳注 28 所述，只有? 的情況似乎會(huì)出現(xiàn)在分相問題中，但這里也處理了另一種情況，因?yàn)閳D 13 和 14 所描述的三種轉(zhuǎn)換一起使得可以將任何給定的相移網(wǎng)絡(luò)轉(zhuǎn)換為損耗補(bǔ)償網(wǎng)絡(luò)。

注：自撰寫此手稿以來(lái)，作者已經(jīng)看到了 Dagnall 和 Rounds? 以及 Farkas, Hallenbeck 和 Stehlick? 的論文，其中討論了相移網(wǎng)絡(luò)的損耗補(bǔ)償?shù)母鞣N其他方法。

附錄

曲線逼近

為 Taylor 和 Tchebycheff 逼近給定? 范圍和給定階數(shù)?，式（9e）和（10c）都可以表述為? 與 1 的偏差，可以寫成以下形式：

對(duì)于（9e）的情況是：

以及對(duì)于（10c）的情況是：

這意味著在兩種情況下， 作為? 的函數(shù)可以寫成如下形式：

其中? 表示函數(shù)? 的第? 次迭代。這里的“第? 次迭代”不僅指整數(shù)值，還包括? 的分?jǐn)?shù)值，因?yàn)? 只有在? 是 2 的整數(shù)冪時(shí)才是整數(shù)。Haldane,? Silberstein,? Hadamard. 已經(jīng)對(duì)非整數(shù)迭代函數(shù)的概念進(jìn)行了一些討論。

不能以同樣的方式解釋逼近函數(shù)? 作為? 的迭代函數(shù)，因?yàn)? 不僅是? 的函數(shù)，還是? 和? 的函數(shù)。但是，如果我們將迭代的概念推廣以適用于兩個(gè)變量的函數(shù)（見 Boole?），則? 可以視為? 的第? 次迭代，其中?。現(xiàn)將說(shuō)明這一點(diǎn)。

由于? 將兩個(gè)獨(dú)立變量變?yōu)橐粋€(gè)依賴變量，只有當(dāng)我們引入第二個(gè)依賴變量時(shí)，才可能進(jìn)行迭代，比如說(shuō)，一個(gè)任意函數(shù)?。然后我們將定義? 和? 為函數(shù)? 和?。此外，我們可以為整數(shù)和非整數(shù)值的? 定義迭代函數(shù)? 和?，作為滿足以下關(guān)系的三個(gè)變量? 和? 的函數(shù)。

如果我們選擇? 作為任意函數(shù)?——恰好與? 無(wú)關(guān)——我們會(huì)看到，如果? 如之前一樣，那么指數(shù)法則（式（12））可以按照式（16）的形式表示。換句話說(shuō)： 和? 可以解釋為? 和? 的第? 次迭代，當(dāng)它們被視為? 和? 的一對(duì)函數(shù)。

有趣的是要注意，如果考慮的是多項(xiàng)式逼近而不是有理函數(shù)逼近，也可以進(jìn)行這樣的解釋。如果? 要通過(guò)多項(xiàng)式? 在范圍? 到? 中逼近，那么第? 階 Tchebycheff 逼近為

且第? 階偏差?。很容易證明? 和?。這些以及與非整數(shù)功能迭代相關(guān)的其他問題都在作者正在準(zhǔn)備發(fā)表的數(shù)學(xué)論文中進(jìn)行了處理。

致謝

感謝 J. G. Flint，Telephone Manufacturing Co. 的首席工程師，允許發(fā)布此論文。作者還想感謝 Miss L. Fosgate 制作了圖紙，以及 Miss L. Fosgate 和 Miss J. Freeman 執(zhí)行和檢查了大量的計(jì)算。非常感謝 Milne-Thomson 和 Hayashi 由 Scientific Computing Service Ltd., London 提供的橢圓函數(shù)表。

參考文獻(xiàn)及腳注

Decimal classification: R246.2? R143. Original manuscript received by the Institute, August 1, 1949.
? Research Laboratories, Telephone Manufacturing Co. Ltd., London, England.
? British Patent No. 301,362, dated August 27, 1927.
? Walter H. Wirkler, U.S. Patent No. 2,173,145, dated Nobember 26, 1937.
? F. Vilbig, "Experimentelle Untersuchung der Verschiebung eines theoretisch beliebig grossen Frequenzbandes um einen bestimmten Phasenwinkel," Telegraphen-Fernsprech-und Funktech., vol. 27, pp. 560-561; December, 1938.
? Ralph V. L. Hartley, U.S. Patent No. 1,666,206, dated January 15,1925.
? M. A. Honnell, "Single-sideband generator," Electronics, vol. 18, pp. 166-168; November, 1945.
? B. E. Lenehan, "A new single sideband carrier system," Elec. Eng., vol. 66, pp. 549-552; June, 1947.
? John F. Byrne, "Polyphase broadcasting," Trans. Elec. Eng., vol. 58, pp. 347-350; July, 1939.
? Paul Loyet, "Experimental polyphase broadcasting," Proc. I.R.E., vol. 30, pp. 213-222; May, 1942.
? K. G. Hodgson, British Patent No. 547,601, dated January 31 1941.
? R. B. Dome, "Wide-band phase shift networks," Electronics, vol. 19, pp. 112-115; December, 1946.
? Donald E. Norgaard, "A new approach to single sideband," QST, vol. 32, pp. 36-43; June, 1948.
? David G. C. Luck, "Properties of some wide-band phase splitting networks," Proc. I.R.E., vol. 37, pp. 147-151; February, 1949.
? Some of the networks obtained as a result of this investigation form the subject of British Patent Application No. 16698/49.
? 這個(gè)假設(shè)不失一般性，因?yàn)槲ㄒ黄渌赡艿倪x擇是? 在?。然而，在這種情況下，我們將有? 在?，然后我們可以將以下討論的結(jié)果應(yīng)用于?，它逼近1就像? 一樣。
? A. Cayley, "Elliptic Functions," 2nd ed., George Bell & Sons, London; 1895.
? K. Hayashi, "Tafeln der Besselschen, Theta, Kugel-undanderer Funktionen," Berlin; 1930.
? L. M. Milne-Thomson, "Die elliptischen Funktionen von Jacobi," Julius Springer, Berlin; 1931.
? 值得注意的是，在濾波器設(shè)計(jì)的情況下，必須使用從模數(shù)? 到較小模數(shù)? 的“第一變換”。盡管這種變換在許多方面與我們問題中使用的變換相似，但它與由式（10a）和（10b）定義的變換不同，因?yàn)樗鼉H對(duì)奇數(shù)? 值導(dǎo)致? 的有理函數(shù)。對(duì)于偶數(shù)? 值，為了使? 成為? 的有理函數(shù)，如 Darlington 所示，必須通過(guò)? 和? 之間更復(fù)雜的關(guān)系來(lái)定義?（請(qǐng)參見腳注 27 中的參考文獻(xiàn)）。
? O. J. Zobel, "Distortion correction in electrical circuits with constant resistance recurrent networks," Bell Sys. Tech. Jour., vol. 7, pp. 438-534; July, 1928.
? W. Saraga, "Attenuation and phase shift equalisers," Wireless Eng., vol. 20, pp. 163-181; April, 1943.
? R. F. Baum, "A contribution to the approximation problem," Proc. I.R.E., vol. 36, pp. 863-869; July, 1948.
? T. Laurent, "New principles for practical computation of filter attenuation by means of frequency transformation," Ericsson Technics, vol. 3, pp. 57-72; 1939.
? E. Rumpelt, "Schablonenverfahren fuer den Entwurf elektrischer Wellenfilter auf der Grundlage der Wellenparameter," Telegraphen Fernsprech. Funk und Fernsch-und Technik, vol. 31, pp. 203210; August, 1942.
? F. Scowen, "Electric Wave Filters," Chapman & Hall Ltd., London, pp. 72-74; 1945. ?
? F. Pyrah, "Constant impedance equalisers: Simplified method of design and standardisation," British P.O. Elec. Eng.'s Jour., vol. 92, pp. 204-211; October, 1939.
? D. N. Truscott, "Logarithmic charts and circuit performance," Electronic Eng., vol. 14, pp. 745-748; May, 1942.
? S. Darlington, "Synthesis of reactance 4-poles which produce prescribed insertion loss characteristics," Jour. Math. Phys., vol. 13, pp. 257-353; September, 1939.
? 在相移網(wǎng)絡(luò)的這種分解的一般情況下，得到的各個(gè)? 值不一定是實(shí)數(shù)，而可能以共軛復(fù)數(shù)對(duì)出現(xiàn)。然后，兩個(gè)相應(yīng)的基本部分可以合并為一個(gè)物理部分，其標(biāo)準(zhǔn)化的串聯(lián)臂電抗為?，其中?。然而，對(duì)于相位分割網(wǎng)絡(luò)，在使用泰勒或切比雪夫逼近法進(jìn)行性能曲線時(shí)，不會(huì)出現(xiàn)復(fù)數(shù)? 值，而且在其他好的逼近中似乎也不會(huì)出現(xiàn)。另一方面，在濾波器設(shè)計(jì)中，它們的出現(xiàn)是規(guī)定的。
? W. A. Marrison, United States Patent No.?, dated September 12, 1933.
? W. Saraga, British Patent No. 594,431, dated May 29, 1945, and U.S. Patent Application No. 670,264.
? E. K. Sandeman, "Phase compensation," Elec. Commun., vol. 7, pp. 309-315; April, 1929.
? M. Wald, "Eine Kunstschaltung zur Verdreifachung des Winkelmasses eines Kreuzgliedes und ihre Anwendung zum Phasenausgleich in Pupinleitungen," Elekt. Nach. vol. 19, pp. 196-199; October, 1942. ?
? A. T. Starr, British Patent No. 342,407, dated October 30, 1929.
? H. W. Bode, "Network Analysis and Feedback Amplifier Design," D. Van Nostrand Company, Inc., New York, N. Y., pp. 216-218; 1945.
? C. H. Dagnall and P. W. Rounds, "Delay equalization of eightkilocycle carrier programme circuits," Bell Sys. Tech. Jour., vol. 23, pp. 181-195; April, 1949.
? F. S. Farkas, F. J. Hallenbeck, and F. E. Stehlick, "Band pass filter, band elimination filter and phase simulating network for carrier programme systems," Bell Sys. Tech. Jour., vol. 28, pp. 196220; April, 1949.
? J. B. S. Haldane, "On the non-linear difference equation?," Proc. Cambridge Phil. Soc., vol. 28, part II, pp. 234243 ; 1932.
? L. Silberstein, "Construction of groups of commutative functions," Phil. Mag., pp. 43-54; January, 1945.
? J. Hadamard, "Two works on iteration and related questions," Bull. Amer. Math. Soc., vol. 50, pp. 67-75; February, 1944.
? G. Boole, "A Treatise on the Calculus of Finite Differences," Macmillan and Co., London, 3rd Ed., p. 17; 1880.

https://120years.net/saraga-generatorwolja-saragagermany1931/

審核編輯：黃飛

?