回到正題:圖靈機。圖靈機能夠識別語言,而圖靈機本身當然也可以由語言描述。什么是語言?給定一個字母表∑,一個{[由∑中的字母組成的序列]的集合}就是∑上的一個語言(為了消除歧義,算式可以加括號,語言當然也可以)。必須清楚這些概念中哪些是有限的,哪些是無限的:一個語言包含的字符串數(shù)可以是有限的也可以是無限的,但一個字母表上的所有語言的數(shù)目是無限的,而語言中任意一個字符串的長度是有限的。
首先要證明的是:一個字母表上所有語言構成的集合不僅是無限的,而且是不可數(shù)的。 這里需要借助無限二進制序列的集合來幫助證明。一個無限二進制序列(即{0,1}組成的無限序列)是一階無限,那么這些序列組成的集合就是“無限×無限”,可以通過對角線方法證明無限二進制序列是不可數(shù)的,也可以將實數(shù)集的元素唯一地映射到無限二進制序列集合。
用后者的方法,可以這樣建立二者之間的映射:二進制序列每4個為一組,用8421BCD碼編碼,4位對應實數(shù)中的一位,再用1111表示小數(shù)點,這樣每個實數(shù)總能映射到一個唯一的二進制序列,既然實數(shù)集不可數(shù),那么無限二進制序列也不可數(shù)。 接下來證明,{無限二進制序列的集合B}與(任意字母表){∑上的所有語言組成的集合L}是同樣規(guī)模的,仍然通過建立映射的方法。設∑上所有字符串的集合按字典序排序成∑*={s1, s2, s3, 。..},L中的每個語言A都對應一個二進制序列b:如果si∈A,bi=1;否則bi=0,這樣的序列稱作A的特征序列。舉個例子,如果∑={a,b},A是所有包含b的串構成的語言,則A的特征序列b如下:
∑*={a, b, aa, ab, ba, bb, aaa, aab,。..} A ={ b, ab, ba, bb, aab,。..} b = 0 1 0 1 1 1 0 1 ,。..
反之,每個二進制序列b也能對應一個唯一的語言,所以L與B等勢,又因為B是不可數(shù)集,所以{∑上的所有語言組成的集合L}也是不可數(shù)的。
好,明確了所有語言構成的集合是不可數(shù)的之后,我要回答下面這個問題:為什么圖靈機集合是可數(shù)的?(reserve:哥德爾配數(shù)法)
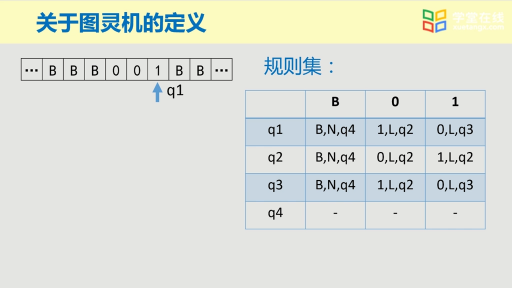
從圖靈機的定義入手,圖靈機是1個7元組(Q,∑,Γ,δ,q0,qaccept,qreject)。每一臺圖靈機總是由有限個字符編碼而成: 1) 有限的狀態(tài)集Q。 2) 有限的輸入字母表∑。 3) 有限的帶字母表Γ。 4) 有限的轉換函數(shù)δ。 5) 1個起始狀態(tài)q0。 6) 有限個接受狀態(tài)qaccept。 7) 有限個拒絕狀態(tài)qreject。 若上述每個元素都用二進制編碼表示,任意一臺圖靈機都只需要有限個二進制位。再將這些二進制串按照字典序排列,就可以得到一個{圖靈機集合}-》自然數(shù)集的一一對應。
好,給定一個字母表∑: [∑上的所有語言]的集合《=》[二進制無限序列]的集合《=》實數(shù)集《=》不可數(shù)集 [所有圖靈機]的集合《=》自然數(shù)集《=》可數(shù)集
有不可數(shù)個語言,卻只有可數(shù)個圖靈機,語言的集合“大于”圖靈機的集合,所以從本質上證明了必然存在圖靈機不能識別的語言。 推論:必然存在圖靈機不能判定的語言。理由是圖靈可判定語言的集合不會大于圖靈可識別語言。 圖靈可判定語言要求更嚴格,所以應該存在這樣的語言:它是圖靈可識別的,但同時不是圖靈可判定的。事實確實如此,圖靈自己就給出了一個: A={《M, ω》 | M描述一臺圖靈機,且M描述的機器接受ω} 首先證明A是圖靈可識別的(形式化證明太過繁瑣,這里只給出很高層次的證明)。設通用圖靈機U這樣運行:U接受參數(shù)《M, ω》,它可根據(jù)圖靈機M的描述模擬M的行為,并在虛擬的M上計算ω。如果M接受ω,那么U進入接受狀態(tài);否則拒絕。
依據(jù)定義以及通用圖靈機的存在性,U能識別A,所以A是圖靈可識別的,證畢。
順著這個證明走下去,如果M本身遇到輸入ω時會陷入循環(huán),那么模擬M的U也會陷入循環(huán),所以U不是判定器。如果U知道M在ω上不停機,那么它可以進入拒絕狀態(tài),問題是它不知道。那么能判定A的圖靈機存在嗎?我們就假設存在H,使得: 1)若M接受ω,則H(《M,ω》) =接受 2)若M不接受ω,則H(《M,ω》) =拒絕 根據(jù)H的定義,無論M接不接受ω,H總能停機。進一步再假設有圖靈機D,以H為子程序,接受一個描述圖靈機的串《M》,在H上運行H(《M,《M》》),并返回相反的結果: 1)若H(《M,《M》》)=接受,則D(《M》)=拒絕 2)若H(《M,《M》》) =拒絕,則D(《M》)=接受 也就是說,如果一臺圖靈機M接受描述它自身的串《M》,那么D(《M》)進入拒絕狀態(tài)。構造這樣一臺奇怪的D是為了讓它做下面這件事情,現(xiàn)在對D輸入描述它自己的串《D》,看看會發(fā)生什么: 1)若D接受《D》,即H(《D,《D》》)=接受,則D(《D》)=拒絕 2)若D拒絕《D》,即H(《D,《D》》) =拒絕,則D(《D》)=接受 到底是接受還是拒絕呢?兜了一個圈子,D繞回原地,產生了矛盾。所以D是不存在的,所以H也是不存在的,語言A不可判定,證畢。
上述證明比較繞,我用一階邏輯再改寫一遍
命題: 1)P:存在語言A的判定器H 2)Q:存在以H為子程序的圖靈機D(描述見上) 已知條件: 1)P→Q:如果有H,總能設計出D 2)┐Q:D是不存在的(證明見上) 證明: 1 P 假設 2 P→Q 已知條件 3 Q 1,2 4 ┐Q 已知條件 5 ┴ 推出矛盾 6 ┐P 假設不成立 上面的證明中,圖靈機D的構造簡直是神來之筆,圖靈怎么想到的?雖然之前的證明沒有直接給出不可判定的語言,但已經(jīng)從數(shù)量上證明有圖靈機不能判定的語言,由于判定器的要求更嚴格,所以可以推斷所有判定器構成的集合小于所有語言構成的集合。這是個與“實數(shù)集的勢大于自然數(shù)集”類似的命題,所以應該能用類似的方法——對角線方法證明。好,嘗試一下。 康托構造映射表格時,表格的每一行由一個自然數(shù)表示這是第幾行,每一列也由一個自然數(shù)標識列數(shù),對角線法構造出來的實數(shù)實際上是一行,然而這一行卻和每一行都不一樣。剛才的證明我們看到,圖靈機集合是可數(shù)集,可將其對應自然數(shù),標識表格的每一行,那么每一列用什么標識呢?怎樣讓列數(shù)與行數(shù)相等呢?行和列的交叉處是什么呢?自然數(shù)/實數(shù)的例子中,每一行由一個自然數(shù)對應一個實數(shù),在這個問題中,行由圖靈機標識了,那么不難想到,每一行應該是一個語言。語言又該如何表示?下面依次回答這些問題。 列應該用什么來標識?在對角線方法中,表格的行列數(shù)一致,行和列都用自然數(shù)集標識。那么首先可以想到既然行用圖靈機標識,那么列也可以用圖靈機標識。但是這樣的話行列交匯處就沒什么意義了,試問隨意挑選的兩臺圖靈機之間能擦出什么火花? 腦子再轉一下,圖靈機與圖靈機之間沒有什么一般化的關系,圖靈機識別的是語言,是字符串,那么將標識列的圖靈機換成描述圖靈機的串,既保持了行列數(shù)一致性,又讓行列交匯處有了非平凡的意義!即,用M1, M2, M3.。.標識第1行、第2行、第3行??再用描述圖靈機的字符串《M1》, 《M2》, 《M3》。..標識第1列、第2列、第3列??行列交匯處就填入accept或reject,表示一臺圖靈機是否接受描述某一臺圖靈機的串!這樣,每一行剛好也就是一個語言,每一個部分的意義都正好是我們想要的。
《M1》
《M2》
《M3》
《M4》
??
M1
accept
reject
reject
reject
M2
reject
reject
accept
M3
accept
accept
reject
accept
M4
reject
Accept
reject
accept
??
為構造對角線準備的表格 走到這一步,離結果就很近了。 若將所有圖靈機和描述它們的串排成表,行列交叉處就是H(Mi,《Mj》)的運行結果。構造圖靈機D,實際上就是用對角線方法選出一行,這一行的第1列與M1相反,第2列與M2相反,第3列與M3相反??所以構造出來的這一行肯定不在這個表中。如果在,這么D所在的行與對角線相交處會出現(xiàn)矛盾!
《M1》
《M2》
《M3》
《M4》
??
D
??
M1
accept
reject
reject
reject
accept
M2
reject
Reject
accept
reject
reject
M3
accept
Accept
Reject
accept
accept
M4
reject
accept
reject
accept
reject
??
D
reject
accept
accept
reject
??
D的每一列都與對角線相反,到它自己與對角線的交匯處產生矛盾 想必圖靈深知語言集比圖靈機集要“大”,一臺圖靈機只能對應一個語言,所以用對角線方法必定能構造出一個所有圖靈機都不能識別的語言。這個語言就是D“識別”的語言,則D的語言肯定不會出現(xiàn)在那個圖靈機和對應語言的表格中。如果強行將這臺“不存在的圖靈機”安插進表格中,必然產生矛盾,矛盾就發(fā)生在D所在行與對角線的相交處。就像康托用對角線方法構造出來的那個實數(shù)無法插入到[自然數(shù)-》實數(shù)]的映射表格中,否則構造出來的那個實數(shù)就與它自己矛盾了,神奇的“圖靈機D”就是這么來的。 圖靈是用圖靈機的術語改寫了對角線方法,在圖靈機上重現(xiàn)康托的思想。
至此,回答了第一個問題:為什么圖靈機也有不可判定的語言,并且還構造了一個這樣的語言,即A={《M, ω》 | M描述一臺圖靈機,且M描述的機器接受ω},A又被稱為接受問題。
語言A是超越圖靈機極限的必然產物,因為圖靈機和語言的內在關系決定了A這樣不能被任何圖靈機判定的語言是存在的。這是本質上的原因,但關于A本身還有一個表象上的原因(之前提到過):之所以不能用圖靈機斷定其它圖靈機是否接受一個串,是因為圖靈機不能斷定其它圖靈機在某個輸入串上計算時是否會停機,這個問題同樣是不可判定的,這就是著名的停機問題(Halting problem)。莊子曰,“吾生也有涯,而知也無涯,以有涯隨無涯,殆已”。以有限的步驟去判定可能無限的計算,殆已。 但由此我產生了一個很大的疑問:為什么圖靈機會不停機?這也是我試圖回答的第二個問題。
 電子發(fā)燒友App
電子發(fā)燒友App































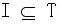













評論