本文來自于第八屆中國機(jī)器人峰會(huì)上張東曉院士題為《科學(xué)機(jī)器學(xué)習(xí)中的知識(shí)嵌入與知識(shí)發(fā)現(xiàn)》的報(bào)告，通過錄音整理而成。

▍1、數(shù)據(jù)驅(qū)動(dòng)模型 1.1 人工智能的發(fā)展

? “人工智能”自1956年被提出后，其發(fā)展過程可以分為三個(gè)階段（圖1）。第一代人工智能主要是知識(shí)驅(qū)動(dòng)，需要定義明確且完備的規(guī)則。這雖然符合人類理解的邏輯，但是無法應(yīng)對(duì)規(guī)則之外的復(fù)雜狀況（如日常對(duì)話）。第二代人工智能主要是數(shù)據(jù)驅(qū)動(dòng)，需要大數(shù)據(jù)、大模型、大算力。例如AlphaGo、Chat GPT，它們依賴大量高質(zhì)量的訓(xùn)練數(shù)據(jù)進(jìn)行自行學(xué)習(xí)，對(duì)于數(shù)據(jù)的要求高，且容易被攻擊或誤導(dǎo)且決策過程不清晰。對(duì)于第三代人工智能的發(fā)展，筆者認(rèn)為應(yīng)該是知識(shí)與數(shù)據(jù)的雙驅(qū)動(dòng)模型，某種意義上是第一代和第二代的結(jié)合。 ?

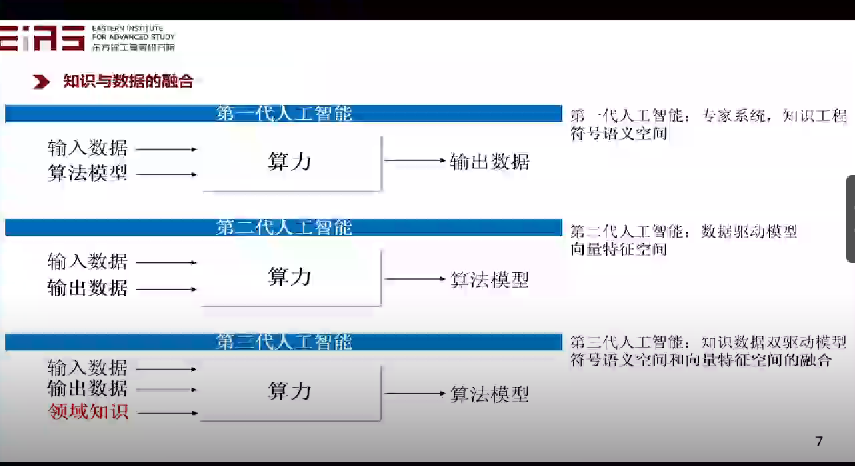
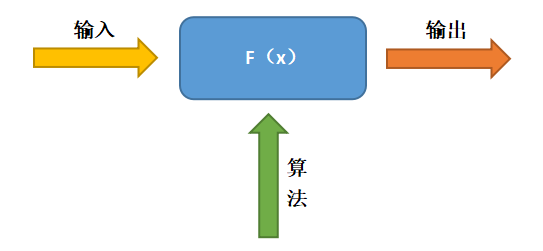
? 圖1 人工智能的發(fā)展 ? 1.2 模型驅(qū)動(dòng)方法 ? 模型驅(qū)動(dòng)方法（圖2）的本質(zhì)是在給定“輸入”的條件下，通過施加一定“條件（或算法）”，得到最終的“輸出”。這些算法可以是確定性的，也可以是隨機(jī)的，而問題的關(guān)鍵是如何獲得模型（方程或公式），即輸入和輸出之間的映射關(guān)系或者模式，進(jìn)而構(gòu)造求解方程的復(fù)雜算法，同時(shí)還需要觀測(cè)值、反問題建模、數(shù)據(jù)同化等模型參數(shù)。 ?

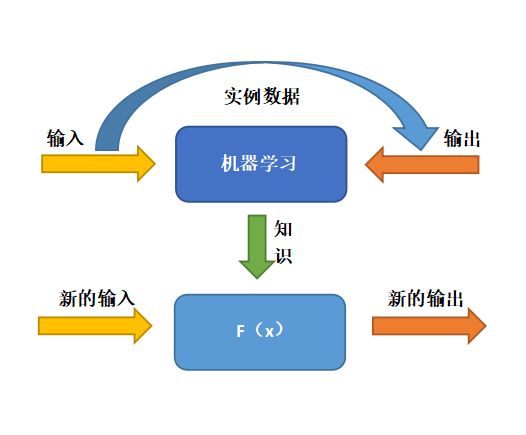
? 圖2 模型驅(qū)動(dòng)方法 ? 1.3 數(shù)據(jù)驅(qū)動(dòng)方法 ? 數(shù)據(jù)驅(qū)動(dòng)意味著在數(shù)據(jù)和模型的天平上側(cè)重于數(shù)據(jù)，例如大數(shù)據(jù)分析、數(shù)據(jù)科學(xué)、機(jī)器學(xué)習(xí)等。數(shù)據(jù)驅(qū)動(dòng)方法（圖3）的本質(zhì)是在沒有對(duì)應(yīng)模式的情況下，通過數(shù)據(jù)進(jìn)行映射的學(xué)習(xí)，建立輸入和輸出之間的映射關(guān)系，現(xiàn)在的人工智能大多都是依靠數(shù)據(jù)驅(qū)動(dòng)。 ?

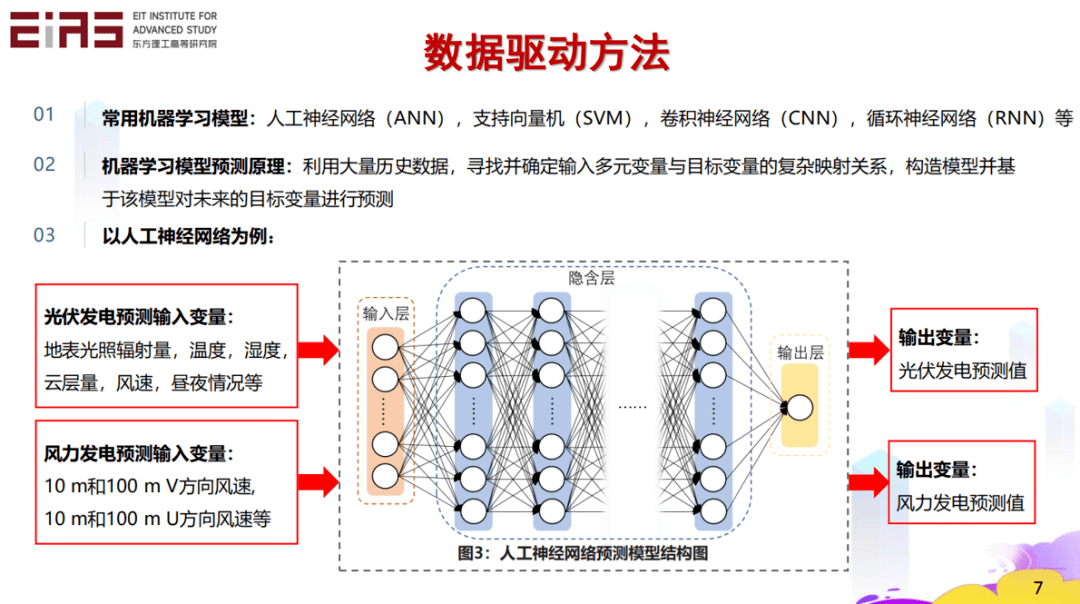
? 圖3 數(shù)據(jù)驅(qū)動(dòng)方法 ? 目前，常用的機(jī)器學(xué)習(xí)模型包括人工神經(jīng)網(wǎng)絡(luò)（ANN）、支持向量機(jī)（SVM）、卷積神經(jīng)網(wǎng)絡(luò)（CNN）、循環(huán)神經(jīng)網(wǎng)絡(luò)（RNN）等，通過利用大量歷史數(shù)據(jù)，尋找并確認(rèn)多元輸入變量與目標(biāo)變量之間復(fù)雜的映射關(guān)系，構(gòu)造模型并基于該模型對(duì)未來的目標(biāo)變量進(jìn)行預(yù)測(cè)。 ? 以人工神經(jīng)網(wǎng)絡(luò)為例，依靠人工神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)模型能夠?qū)ξ磥砉夥l(fā)電值進(jìn)行預(yù)測(cè)（圖4）。結(jié)合歷史發(fā)電量和歷史天氣狀況（地表光照輻射量、溫度、濕度等），通過大數(shù)據(jù)、人工智能的機(jī)器學(xué)習(xí)辦法建立一種映射關(guān)系，基于此映射關(guān)系和天氣預(yù)報(bào)數(shù)據(jù)，預(yù)測(cè)未來光伏發(fā)電值。 ?

? 圖4 基于人工神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)未來光伏發(fā)電值 ? 此外，筆者基于兩個(gè)獨(dú)立的光伏發(fā)電站獲取的數(shù)據(jù)進(jìn)行試驗(yàn)，將17個(gè)與光伏發(fā)電相關(guān)的天氣變量（地表光照輻射量、溫度、濕度、云層量、大氣壓強(qiáng)等）作為輸入的變量，采用最大最小歸一化（min-max normalization）方法，將數(shù)據(jù)限制在01之間，根據(jù)730天的訓(xùn)練數(shù)據(jù)集與91天的測(cè)試數(shù)據(jù)集的天氣數(shù)據(jù)和對(duì)應(yīng)光伏發(fā)電量數(shù)據(jù)進(jìn)行交叉驗(yàn)證設(shè)置，最終得到預(yù)測(cè)模型并實(shí)現(xiàn)光伏發(fā)電預(yù)測(cè)，預(yù)測(cè)的準(zhǔn)確率高達(dá)97%。（圖5） ?

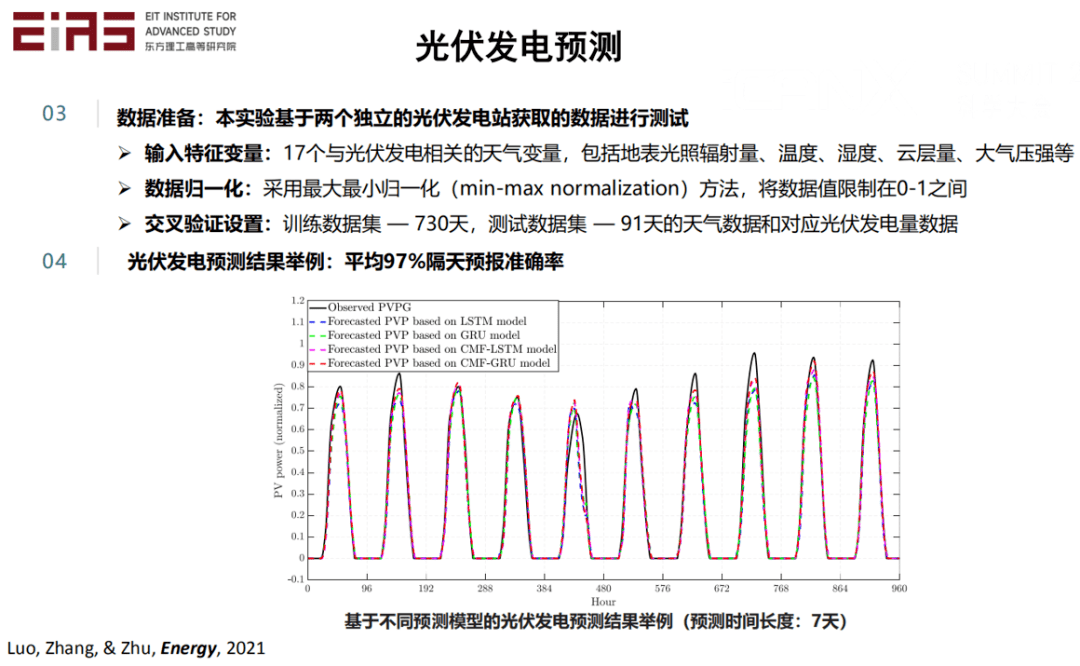
? 圖5 基于不同預(yù)測(cè)模型的光伏發(fā)電預(yù)測(cè)結(jié)果舉例（預(yù)測(cè)時(shí)間長度：7天） ? 1.4 研究背景與意義——數(shù)據(jù)驅(qū)動(dòng)（連接主義AI）的局限性 ? 1.4.1 現(xiàn)實(shí)場景數(shù)據(jù)極度稀缺 ? 在現(xiàn)實(shí)應(yīng)用場景中建立深度學(xué)習(xí)網(wǎng)絡(luò)，待訓(xùn)練參數(shù)量往往上萬甚至上百萬。以Chat GPT3為例，它有96層的神經(jīng)網(wǎng)絡(luò)，12288個(gè)隱層維度，1750億個(gè)參數(shù)，如此大的模型就需要大算力進(jìn)行工作。在許多工業(yè)場景中，數(shù)據(jù)不僅有限，而且昂貴，以農(nóng)業(yè)領(lǐng)域?yàn)槔瑢?duì)于地下資源勘探與開發(fā)重要的側(cè)井曲線，打一口井進(jìn)行測(cè)量需要好幾千萬元；做一組吸附解析的實(shí)驗(yàn)要花很長的時(shí)間，很難獲得足夠的數(shù)據(jù)基于數(shù)據(jù)驅(qū)動(dòng)方法對(duì)此類問題建模。 ?

1.4.2均方誤差等指標(biāo)的局限性

? 數(shù)據(jù)驅(qū)動(dòng)模型中，均方誤差（Mean Squared Error，MSE）等指標(biāo)帶來的局限性同樣不容忽視，MSE對(duì)誤差的物理過程是沒有區(qū)分的，比如一個(gè)系統(tǒng)無論是熵增還是熵減，對(duì)于MSE來講都是一樣的，但對(duì)于一個(gè)物理系統(tǒng)來講是不同的。基于數(shù)據(jù)平均意義上的指標(biāo)往往會(huì)忽略物理過程，例如對(duì)于污染擴(kuò)散的預(yù)測(cè)，一個(gè)區(qū)域的污染濃度增加，另一區(qū)域的污染濃度減少，平均的污染濃度可以不變，但事實(shí)并非如此。 ? ? 1.4.3 易被攻擊與誤導(dǎo) ? 許多數(shù)據(jù)驅(qū)動(dòng)的模型是不具備常識(shí)、缺少知識(shí)的。例如在對(duì)抗樣本的問題中，圖片本來是一個(gè)熊貓，加上一點(diǎn)輕微的噪音以后，機(jī)器可能會(huì)認(rèn)為它是一個(gè)長臂猿，但這種識(shí)別錯(cuò)誤不會(huì)發(fā)生在人的身上（圖6）。 ?

? 圖6 數(shù)據(jù)驅(qū)動(dòng)模型的局限性 ? 早期的人工智能模型都是知識(shí)驅(qū)動(dòng)的，例如DENDRAL系統(tǒng)對(duì)于有機(jī)化學(xué)結(jié)構(gòu)的分析、MYCIN系統(tǒng)對(duì)于血液傳染病的診斷、Deep Blue戰(zhàn)勝國際象棋世界冠軍，但它們都是按照規(guī)則研制而成，只能解決規(guī)則范圍內(nèi)的問題，難以處理復(fù)雜的現(xiàn)實(shí)問題。這也是基于數(shù)據(jù)驅(qū)動(dòng)的人工智能模型被廣泛推廣的原因之一。 ? 如今，數(shù)據(jù)驅(qū)動(dòng)方法尚且存在許多的不足，僅以能源行業(yè)為例，行業(yè)面臨著對(duì)模型的魯棒性和解釋性要求高、數(shù)據(jù)采集費(fèi)時(shí)且成本高昂等問題，只有構(gòu)建知識(shí)與數(shù)據(jù)的雙驅(qū)動(dòng)模型——既有人工智能技術(shù)，也有相關(guān)領(lǐng)域知識(shí)，還有觀測(cè)數(shù)據(jù)，相互的融合才能實(shí)現(xiàn)一個(gè)智慧能源系統(tǒng)（圖7），提升模型精度和魯棒性，降低對(duì)數(shù)據(jù)的需求。而智慧能源系統(tǒng)作為知識(shí)與數(shù)據(jù)的雙驅(qū)動(dòng)模型，一方面，需要通過理論指導(dǎo)的數(shù)據(jù)驅(qū)動(dòng)模型（知識(shí)嵌入），從而構(gòu)建具有物理常識(shí)的AI模型；另一方面，利用人工智能進(jìn)行數(shù)據(jù)驅(qū)動(dòng)的模型挖掘（知識(shí)發(fā)現(xiàn)），從觀測(cè)數(shù)據(jù)中提煉物理知識(shí)。當(dāng)知識(shí)嵌入和知識(shí)發(fā)現(xiàn)可以形成一個(gè)閉環(huán)，實(shí)現(xiàn)知識(shí)和數(shù)據(jù)的融合，能夠很好地解決仿真模擬，反問題，可解釋性等問題。 ?

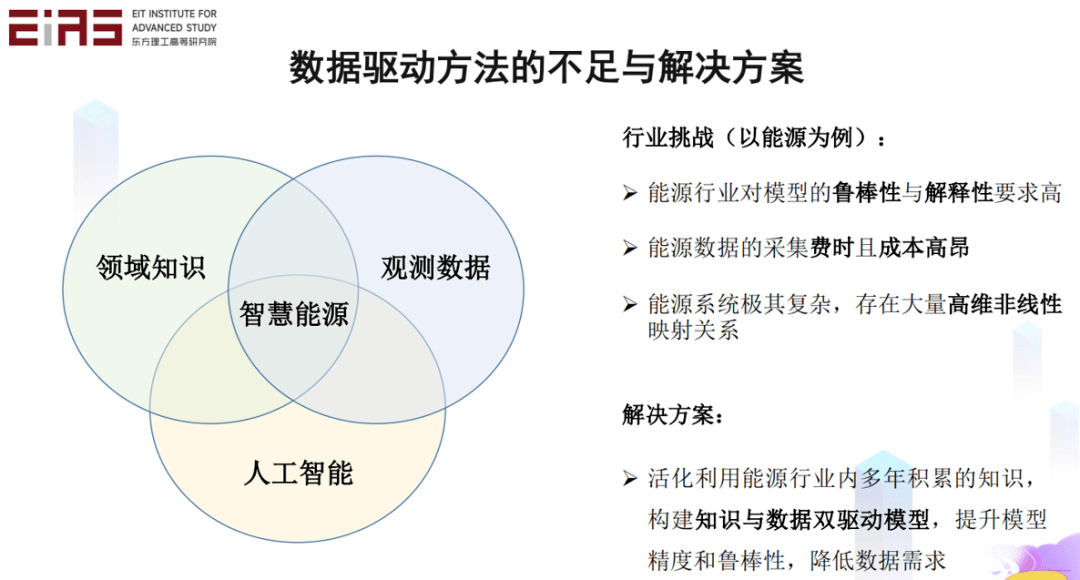
? 圖7 智慧能源系統(tǒng) ? ▍2、理論指導(dǎo)的數(shù)據(jù)驅(qū)動(dòng)模型（知識(shí)嵌入） ? 理論指導(dǎo)的數(shù)據(jù)驅(qū)動(dòng)模型是指在建模全流程中進(jìn)行知識(shí)嵌入，構(gòu)建具有物理常識(shí)的AI模型。圖8所示為機(jī)器學(xué)習(xí)建模全流程的知識(shí)嵌入方法。一方面借助機(jī)器學(xué)習(xí)的強(qiáng)擬合能力，描述變量間高維復(fù)雜映射關(guān)系，另一方面利用能源領(lǐng)域內(nèi)的先驗(yàn)知識(shí)，保證預(yù)測(cè)結(jié)果符合物理機(jī)理，構(gòu)建物理上合理、數(shù)學(xué)上準(zhǔn)確、計(jì)算上穩(wěn)定高效的模型。因此，知識(shí)嵌入的核心問題在于四個(gè)方面，一是復(fù)雜形式控制方程的嵌入方法；二是控制方程以外的通用知識(shí)的嵌入方法；三是不規(guī)則物理場的知識(shí)嵌入方法；四是損失函數(shù)中正則項(xiàng)權(quán)重的自動(dòng)調(diào)整策略。 ? ? 以智慧能源系統(tǒng)為例，在建模過程的多個(gè)環(huán)節(jié)都可以進(jìn)行知識(shí)嵌入，在數(shù)據(jù)預(yù)處理環(huán)節(jié)，可以嵌入物理約束和人類的領(lǐng)域知識(shí)和先驗(yàn)經(jīng)驗(yàn)；在模型結(jié)構(gòu)設(shè)計(jì)環(huán)節(jié)，可以基于領(lǐng)域知識(shí)調(diào)整模型的網(wǎng)絡(luò)結(jié)構(gòu)或者拓?fù)浣Y(jié)構(gòu)；在模型效果評(píng)估環(huán)節(jié)，可以構(gòu)建特殊設(shè)計(jì)的損失函數(shù)。 ?

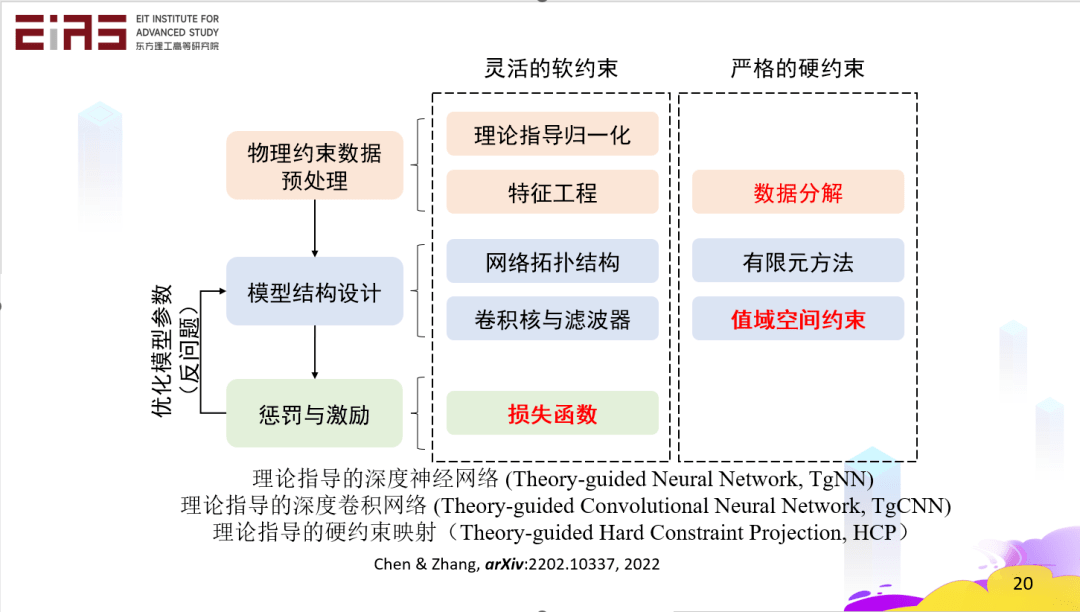
? 圖8 機(jī)器學(xué)習(xí)建模全流程的知識(shí)嵌入方法示意圖 ? 2.1 在數(shù)據(jù)預(yù)處理環(huán)節(jié)嵌入領(lǐng)域知識(shí) ? 在電網(wǎng)負(fù)荷預(yù)測(cè)模型（圖9）的研究中，電力系統(tǒng)基于機(jī)器學(xué)習(xí)模型中的集合神經(jīng)網(wǎng)絡(luò)（ENN）和長短期記憶神經(jīng)網(wǎng)絡(luò)（LSTM），在數(shù)據(jù)預(yù)處理環(huán)節(jié)引入電力負(fù)荷比值分解的方法來嵌入知識(shí)，把電力負(fù)荷數(shù)據(jù)分解成一個(gè)大的趨勢(shì)和局部擾動(dòng)，大的趨勢(shì)反映了預(yù)測(cè)區(qū)域的內(nèi)在模式，比如能源結(jié)構(gòu)、產(chǎn)業(yè)結(jié)構(gòu)、人口密度等，是根據(jù)歷史數(shù)據(jù)和專家經(jīng)驗(yàn)來確定的。局部擾動(dòng)則是系統(tǒng)受到天氣等外驅(qū)力影響下所產(chǎn)生的變化，通過數(shù)據(jù)驅(qū)動(dòng)模型來預(yù)測(cè)。最終，將大的趨勢(shì)和小的擾動(dòng)結(jié)合。 ?

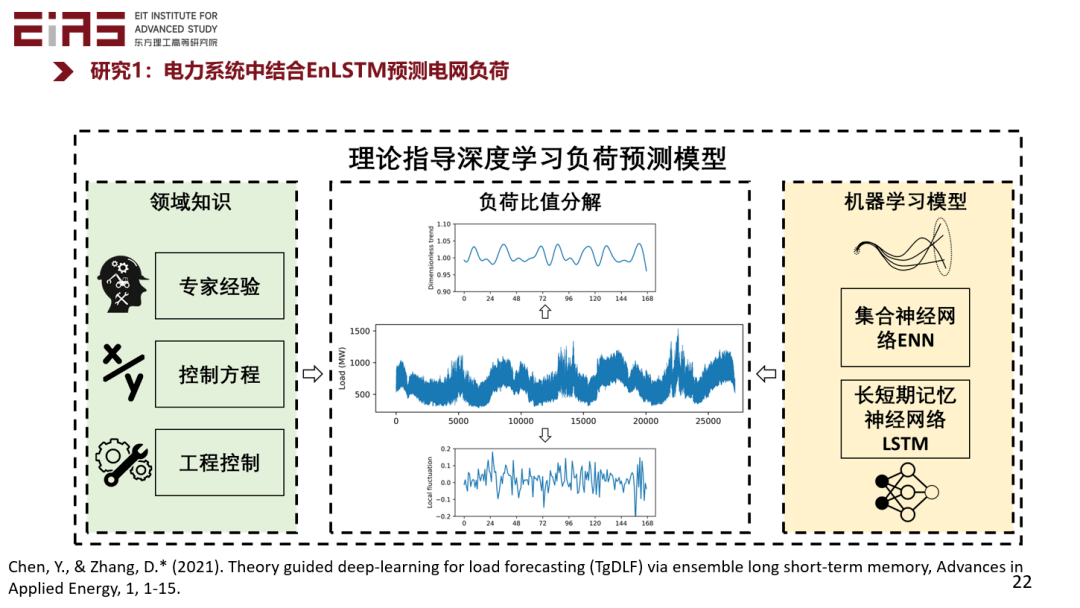
? 圖9 電網(wǎng)負(fù)荷預(yù)測(cè)模型 ? 使用上述方法，基于北京12個(gè)區(qū)歷史1362天小時(shí)級(jí)別的真實(shí)電力負(fù)荷數(shù)據(jù)進(jìn)行試驗(yàn)驗(yàn)證，預(yù)測(cè)北京市豐臺(tái)區(qū)電力負(fù)荷（圖10），其中紅色為預(yù)測(cè)值，黑色為真實(shí)值，灰色為置信區(qū)間，即使沒有利用預(yù)測(cè)區(qū)域的數(shù)據(jù)，僅使用周邊區(qū)域的數(shù)據(jù)進(jìn)行訓(xùn)練，模型也能夠非常準(zhǔn)確地進(jìn)行電力負(fù)荷預(yù)測(cè)。 ?

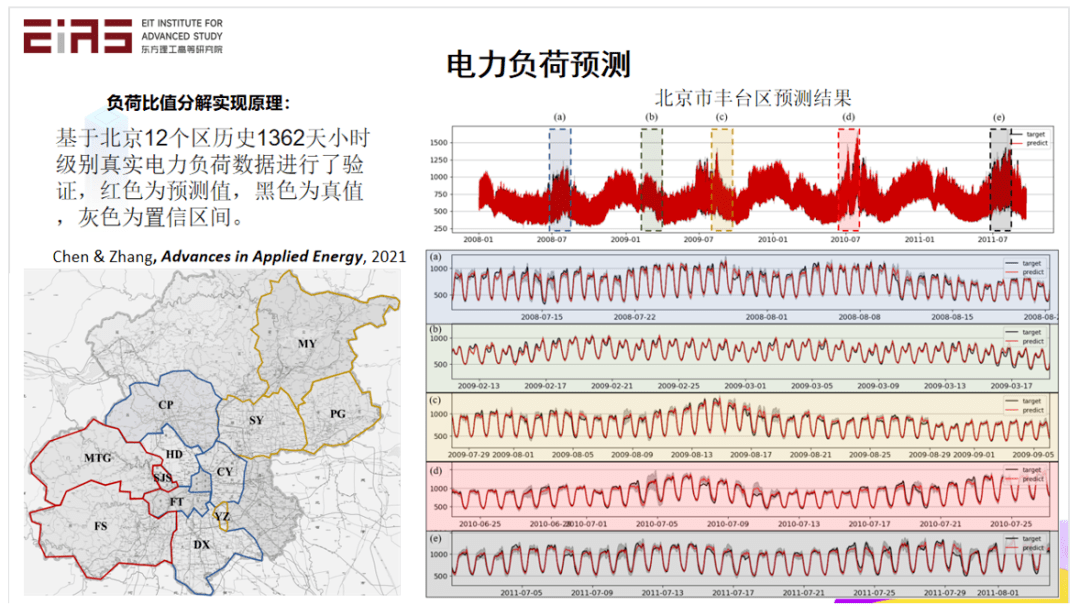
? 圖10 北京市豐臺(tái)區(qū)電力負(fù)荷預(yù)測(cè)結(jié)果 ? 2.2?在模型效果評(píng)估階段嵌入領(lǐng)域知識(shí) ? 2.2.1 將概率分布信息作為約束嵌入AI模型 ? 與光伏類似，風(fēng)力發(fā)電也具有強(qiáng)烈的隨機(jī)性和波動(dòng)性，風(fēng)功率的準(zhǔn)確預(yù)測(cè)有助于提高電網(wǎng)運(yùn)行的穩(wěn)定性，能夠有效地幫助電網(wǎng)調(diào)度部門做好各類電源的調(diào)度計(jì)劃。對(duì)此，筆者及其團(tuán)隊(duì)成員研發(fā)了融合領(lǐng)域知識(shí)的風(fēng)功率預(yù)測(cè)模型（圖11），根據(jù)風(fēng)電區(qū)域的風(fēng)向、風(fēng)機(jī)轉(zhuǎn)速、槳距角和實(shí)際風(fēng)功率等數(shù)據(jù)建立精準(zhǔn)風(fēng)功率預(yù)測(cè)模型，并嵌入風(fēng)功率曲線這一物理知識(shí)以提高預(yù)測(cè)準(zhǔn)確度。由于實(shí)際工況復(fù)雜，風(fēng)功率曲線并非一個(gè)一對(duì)一的映射，而是需要用描述風(fēng)速和發(fā)電功率之間關(guān)系的概率分布函數(shù)來表征。從歷史數(shù)據(jù)得到先驗(yàn)的風(fēng)功率曲線，然后通過改造損失函數(shù)，將其嵌入到模型的訓(xùn)練過程中，最終結(jié)合天氣預(yù)報(bào)與氣象觀測(cè)站，形成一套軟硬結(jié)合的物理與數(shù)據(jù)雙驅(qū)動(dòng)的風(fēng)力發(fā)電功率預(yù)測(cè)產(chǎn)品。 ? ?

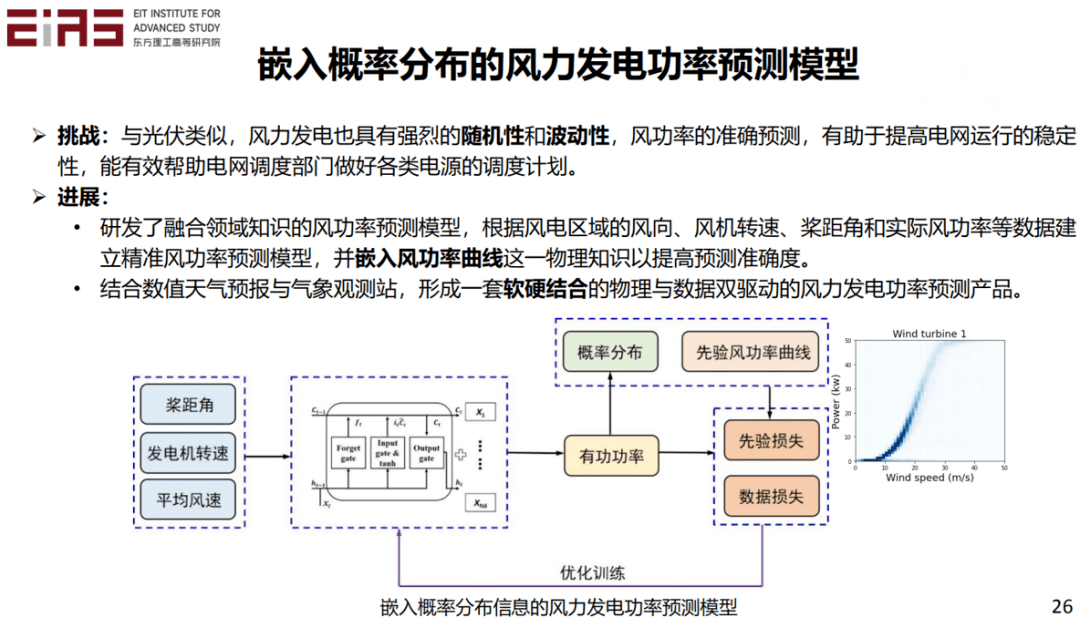
? 圖11 嵌入概率分布信息的風(fēng)力發(fā)電功率預(yù)測(cè)模型 ? 通過這種方法建立的人工智能模型不僅具有數(shù)據(jù)驅(qū)動(dòng)的優(yōu)勢(shì)，還能保證輸出結(jié)果符合先驗(yàn)的概率分布。將基于氣象數(shù)據(jù)和風(fēng)功率曲線的風(fēng)功率預(yù)測(cè)結(jié)果與真實(shí)值進(jìn)行對(duì)比（圖12），預(yù)測(cè)準(zhǔn)確率高于90%。 ?

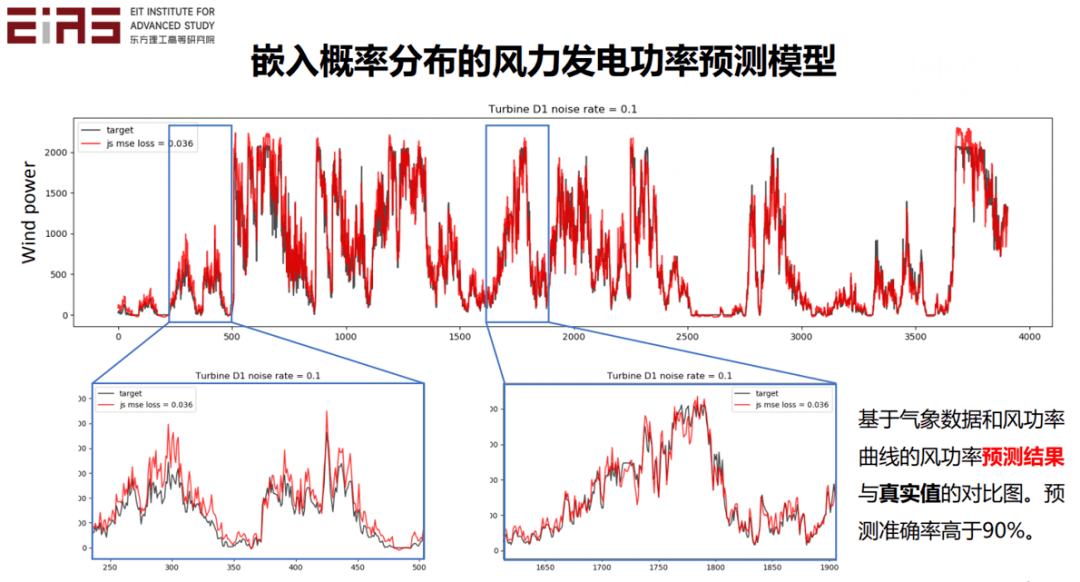
? 圖12 數(shù)據(jù)對(duì)比圖 ? 2.2.2 將控制方程作為約束嵌入AI模型 ? 在模型效果評(píng)估階段嵌入領(lǐng)域知識(shí)的方法，主要是基于改進(jìn)損失函數(shù)的方法將控制方程作為約束嵌入到人工智能的模型中，這對(duì)于大數(shù)據(jù)量的求解非常有幫助，并且能減小預(yù)測(cè)的誤差。 ?

基于理論指導(dǎo)神經(jīng)網(wǎng)路（Theory-guided Neural Network，TgNN）的替代模型（圖13）具有理論指導(dǎo)的深度學(xué)習(xí)模型框架，將物理規(guī)律、工程控制、專家經(jīng)驗(yàn)等先驗(yàn)信息融合到深度學(xué)習(xí)模型的訓(xùn)練中，實(shí)現(xiàn)更高的預(yù)測(cè)準(zhǔn)確性、更好的可解釋性、更強(qiáng)的魯棒性。在理論指導(dǎo)下，TgNN替代模型可以在較少的訓(xùn)練數(shù)據(jù)的情況下進(jìn)行構(gòu)建，減小對(duì)數(shù)據(jù)量的依賴，例如，用基于TgNN/物理信息神經(jīng)網(wǎng)絡(luò)（Physics-informed Nerual Network，PINN）替代模型進(jìn)行不同滲透率場實(shí)現(xiàn)的解的預(yù)測(cè)（圖14），訓(xùn)練過程中僅使用30個(gè)現(xiàn)實(shí)提供的訓(xùn)練數(shù)據(jù)就達(dá)到了足夠的精度。

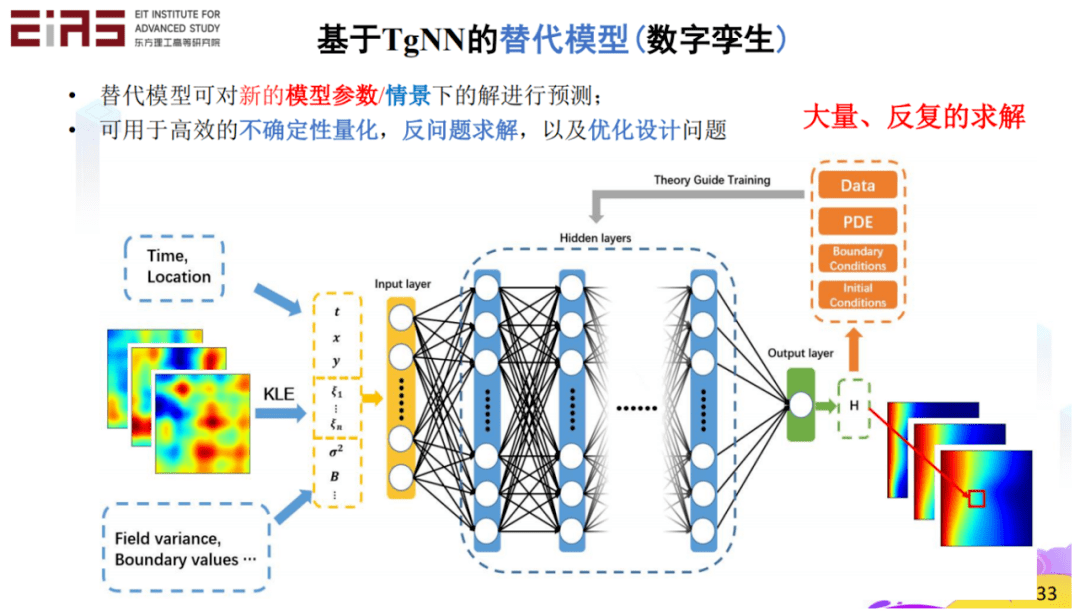
? 圖13 基于TgNN的替代模型 ?

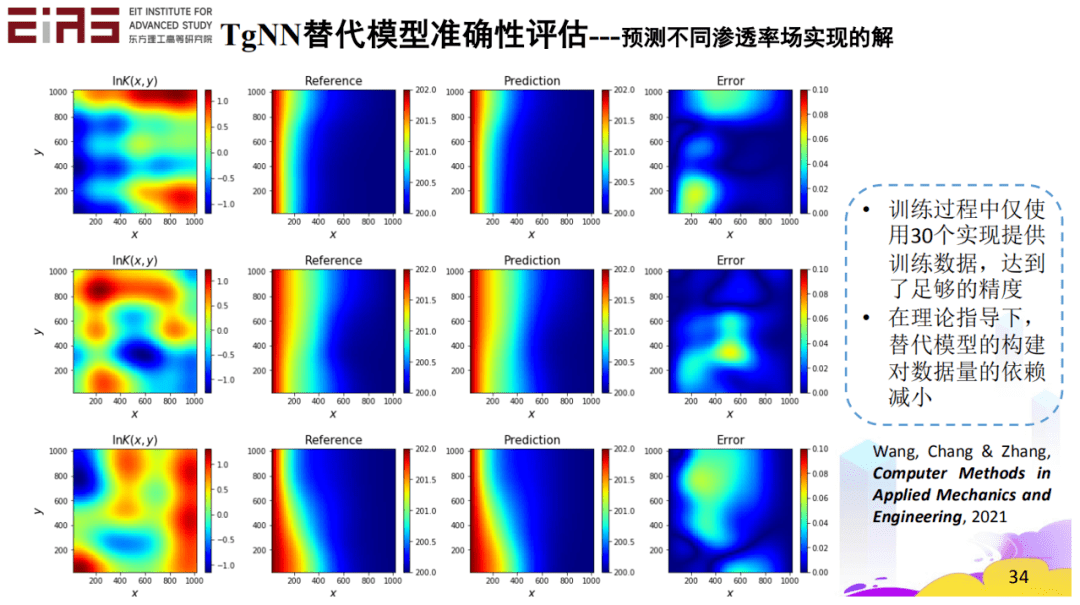
? 圖14 TgNN/PINN替代模型準(zhǔn)確性評(píng)估——預(yù)測(cè)不同滲透率場實(shí)現(xiàn)的解 ? 此外，將TgNN替代模型應(yīng)用于工程問題中的不確定性量化（圖15），能夠大大提升不確定性量化任務(wù)的效率。以蒙特卡羅方法（MC）作為參考值，使用KL展開生成10000個(gè)實(shí)現(xiàn)，使用MODFLOW求解，所需時(shí)間約為1.74h；使用TgNN替代模型預(yù)測(cè)求解，因?yàn)樯窠?jīng)網(wǎng)絡(luò)的預(yù)測(cè)速度很快，因此只需要大約9min，TgNN替代模型顯著提高了不確定性量化的效率。 ?

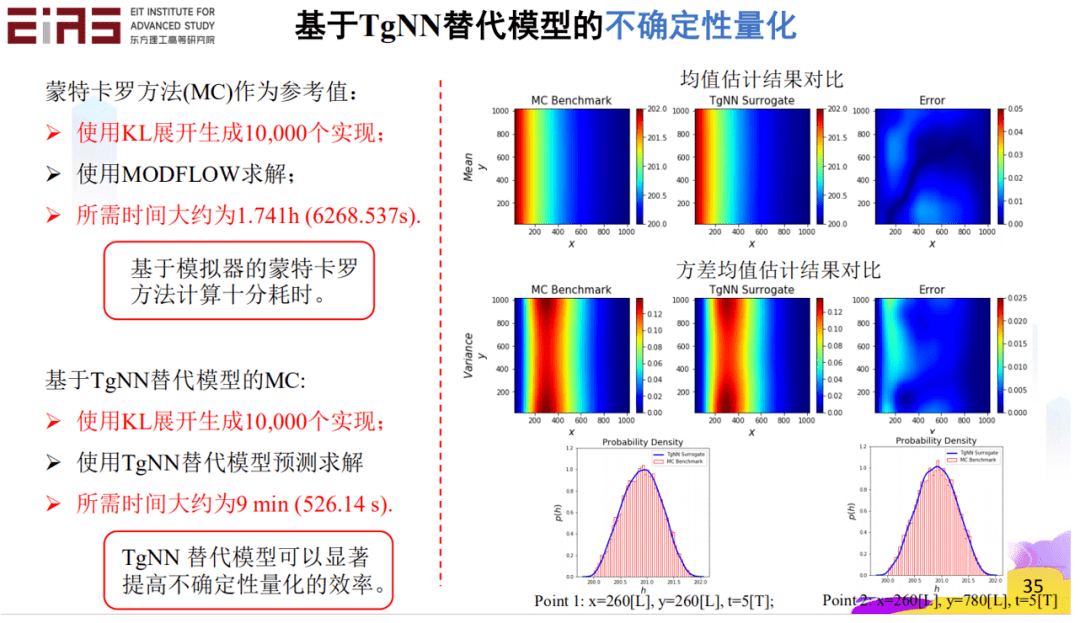
? 圖15 基于TgNN/PINN替代模型的不確定性量化 ? 面對(duì)復(fù)雜問題，例如兩相流（油—水、油—?dú)猓﹩栴}——同時(shí)預(yù)測(cè)壓力和飽和度（圖16、17），在兩個(gè)方程組的情況下，利用控制方程也能進(jìn)行高效預(yù)測(cè)。 ?

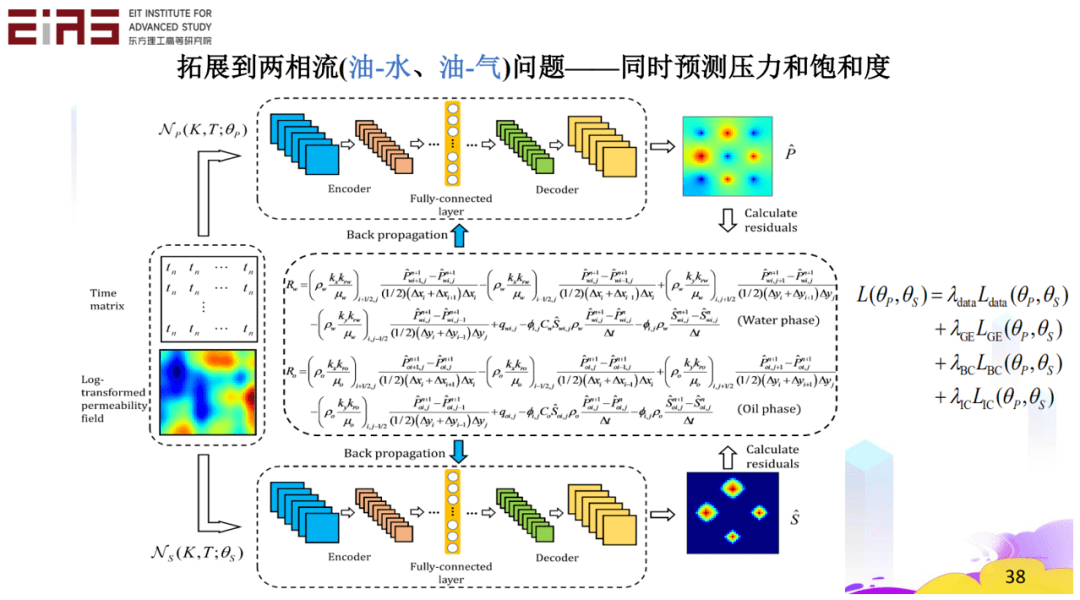
? 圖16 兩相流（油—水、油—?dú)猓﹩栴} ?

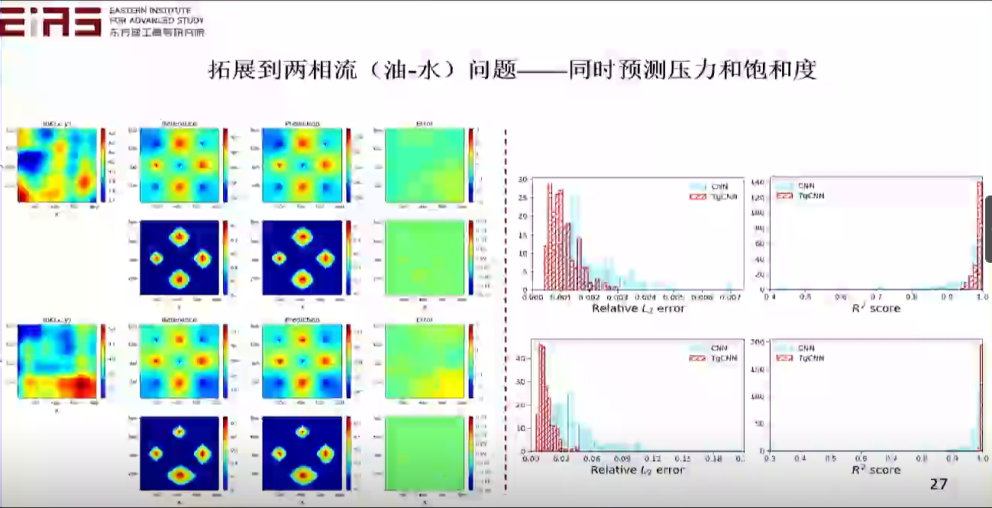
? 圖17 兩相流（油—水、油—?dú)猓﹩栴}預(yù)測(cè)結(jié)果 ? 2.3 在模型結(jié)構(gòu)設(shè)計(jì)和效果評(píng)估階段嵌入領(lǐng)域知識(shí) ? 利用軟約束嵌入控制方程雖然易于實(shí)現(xiàn)但只能產(chǎn)生平均意義上符合物理約束的預(yù)測(cè)結(jié)果，相比之下，硬約束能通過映射的方式（圖18），利用投影矩陣，將模型輸出值映射到嚴(yán)格符合物理機(jī)理的值域，保證局部嚴(yán)格滿足物理約束，具有更高的收斂速度和更低的數(shù)據(jù)需求。 ?

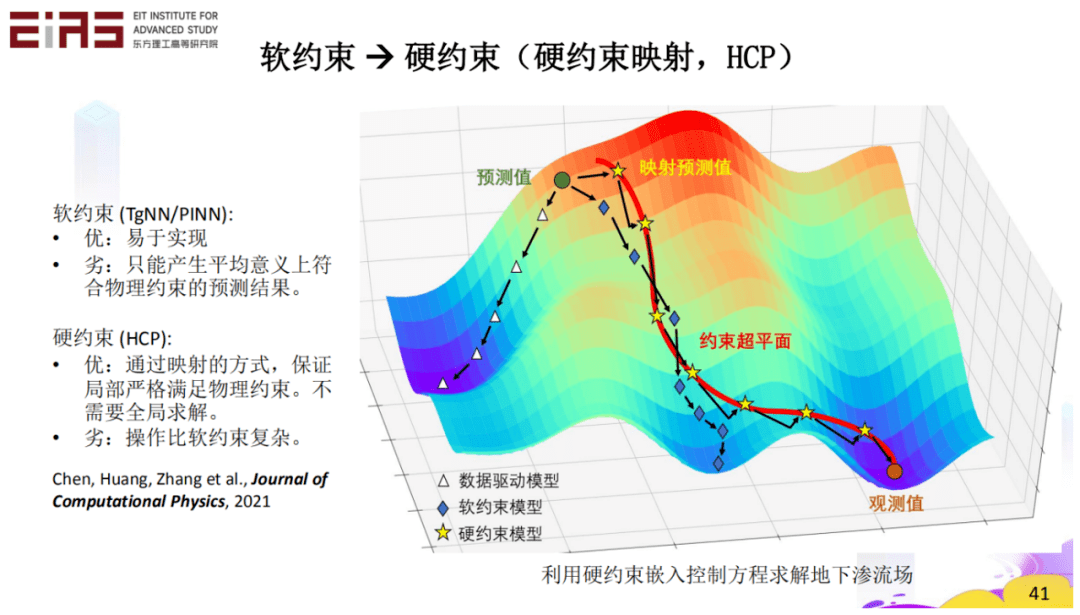
? 圖18 利用硬約束嵌入控制方程求解地下滲流場的硬約束映射 ? ?

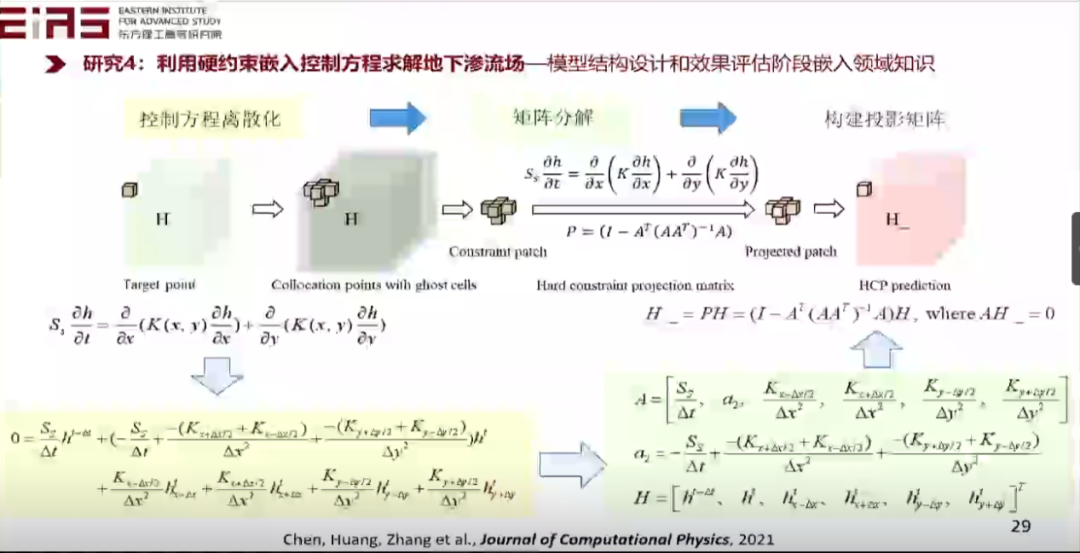
? 圖19 利用硬約束嵌入控制方程求解地下滲流場投影矩陣構(gòu)建 ? ?

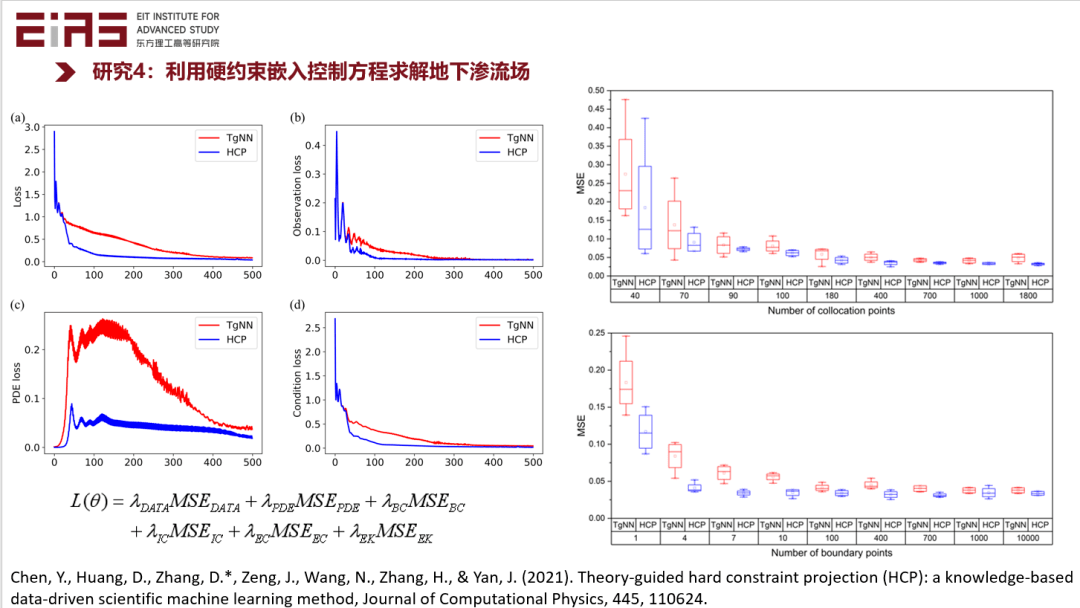
? 圖20 利用硬約束嵌入控制方程求解地下滲流場的效果評(píng)估 ? ? 在實(shí)際嵌入知識(shí)的過程中存在大量難點(diǎn)，尤其是嵌入復(fù)雜方程，如具有分式結(jié)構(gòu)或者復(fù)合函數(shù)的方程，難以直接利用神經(jīng)網(wǎng)絡(luò)的自動(dòng)微分機(jī)制求梯度，因此也難以直接嵌入到人工智能模型中，因此，筆者在研究的過程中開發(fā)了自動(dòng)化知識(shí)嵌入框架及工具包（圖21、22）。 ?

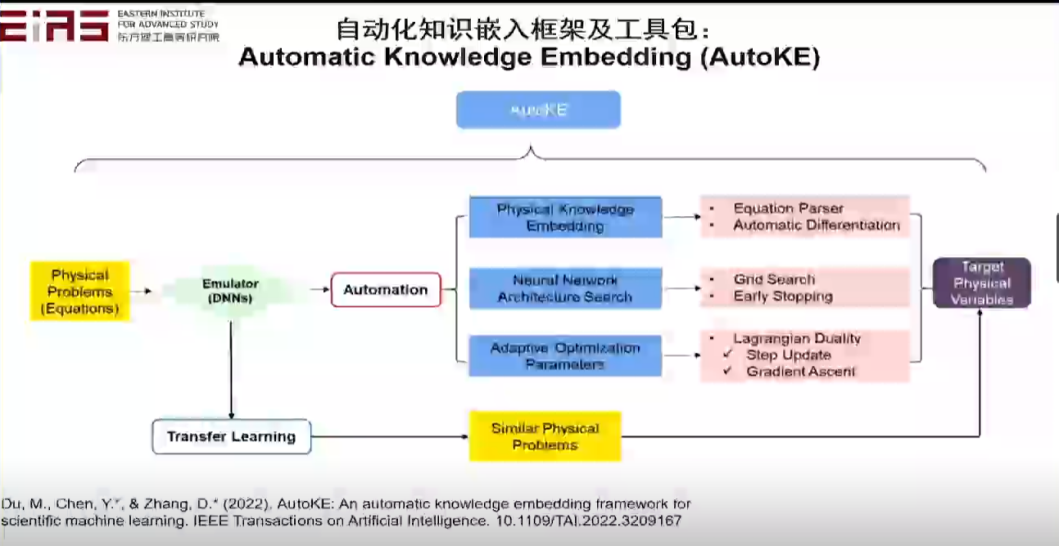
? 圖21 自動(dòng)化知識(shí)嵌入框架及工具包（1） ? ?

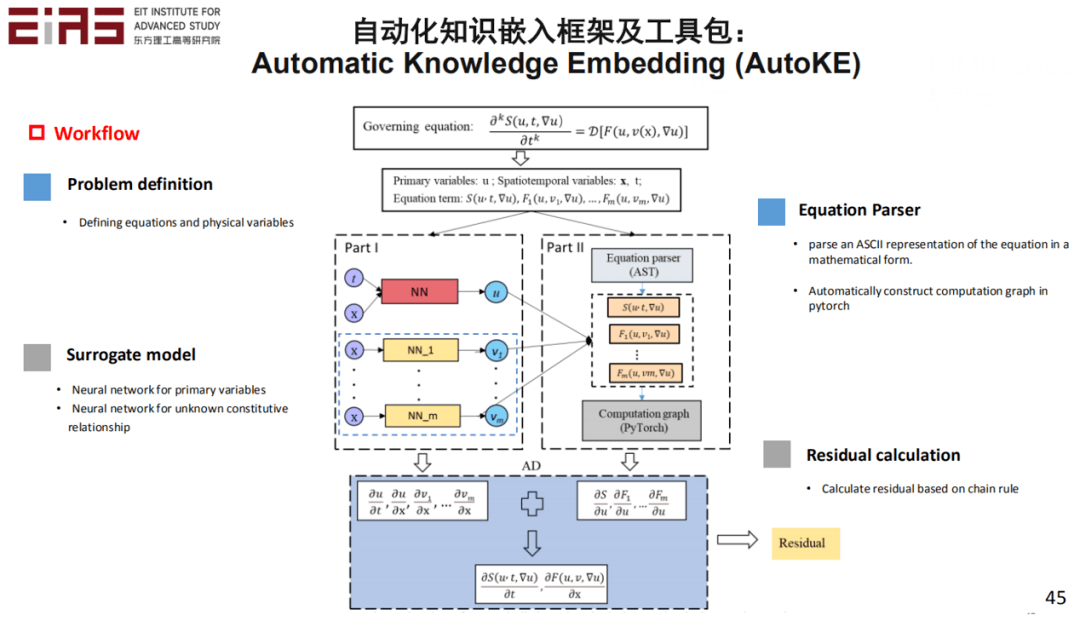
? 圖22 自動(dòng)化知識(shí)嵌入框架及工具包（2） ? ▍3、數(shù)據(jù)驅(qū)動(dòng)的模型挖掘（知識(shí)發(fā)現(xiàn)） ? 知識(shí)發(fā)現(xiàn)是指從觀測(cè)數(shù)據(jù)中提煉物理知識(shí)，借助人工智能自動(dòng)探索物理原理，推進(jìn)人類認(rèn)知前沿，同時(shí)迭代利用發(fā)現(xiàn)的知識(shí)，即結(jié)合知識(shí)嵌入，形成知識(shí)和數(shù)據(jù)的閉環(huán)系統(tǒng)。其核心問題在于五個(gè)方面：一是控制方程的靈活表示方法以及優(yōu)化算法；二是復(fù)雜結(jié)構(gòu)控制方程的挖掘方法；三是復(fù)雜系數(shù)控制方程的挖掘方法；四是針對(duì)稀缺且嘈雜的數(shù)據(jù)的挖掘方法；五是從實(shí)驗(yàn)數(shù)據(jù)中挖掘全新的控制方程。 ? 3.1 從行星運(yùn)動(dòng)三大定律的提出看控制方程的挖掘 ? 第谷耗時(shí)38年觀測(cè)火星軌跡數(shù)據(jù)，但是他沒有找到規(guī)律；第谷的學(xué)生開普勒耗時(shí)17年研究數(shù)據(jù)，最后總結(jié)出行星運(yùn)動(dòng)三大定律；在此基礎(chǔ)上，牛頓發(fā)現(xiàn)了萬有引力定律。而AI技術(shù)的發(fā)展將大大加快這一進(jìn)程，根據(jù)數(shù)據(jù)找出內(nèi)在規(guī)律，這一過程需要發(fā)揮機(jī)器學(xué)習(xí)算法描述高維非線性映射的優(yōu)勢(shì)，從實(shí)驗(yàn)數(shù)據(jù)中直接挖掘新的知識(shí)，加深對(duì)物理本質(zhì)的理解。 ? 3.2 從人工智能的發(fā)展看控制方程的挖掘 ? 神經(jīng)網(wǎng)絡(luò)作為傳統(tǒng)的機(jī)器學(xué)習(xí)的研究方向，實(shí)際上是一種黑盒模式（圖23），其可解釋性差，但隨著人工智能的發(fā)展，通過模型挖掘顯式表達(dá)出神經(jīng)網(wǎng)絡(luò)的內(nèi)部邏輯（控制方程），能夠提高可解釋性。 ? ?

? 圖23 神經(jīng)網(wǎng)絡(luò) ? ? 3.3 數(shù)據(jù)驅(qū)動(dòng)的偏微分方程挖掘

利用機(jī)器學(xué)習(xí)方法從數(shù)據(jù)中直接發(fā)現(xiàn)潛在的物理過程及其控制方程。

3.3.1 封閉候選集方法：稀疏回歸 ? 在具備數(shù)據(jù)的情況下就可以得到它的梯度和各階導(dǎo)數(shù)。理論上系統(tǒng)中可能存在許多項(xiàng)，但是實(shí)際的方程是稀疏的，它只有其中的幾項(xiàng)，其他的項(xiàng)的系數(shù)都是0，所以那些項(xiàng)是不存在的。這樣問題就轉(zhuǎn)化成，在一個(gè)系統(tǒng)中如何找到稀疏的向量，而且它的系數(shù)也能同時(shí)找出來。利用稀疏回歸進(jìn)行偏微分方程的挖掘（圖24），能夠從數(shù)據(jù)中識(shí)別出時(shí)間導(dǎo)數(shù)、潛在偏微分方程的項(xiàng)以及稀疏的系數(shù)向量。 ?

? 圖24 稀疏回歸挖掘偏微分方程 ? 3.3.2 半開放候選集方法：遺傳算法 ? 稀疏回歸的前提是項(xiàng)（候選集）的存在，在項(xiàng)不完全存在的情況下，則需要通過遺傳算法（Genetic Algorithm，GA）挖掘控制方程。遺傳算法是一種最基本的進(jìn)化算法，它是模擬達(dá)爾文生物進(jìn)化理論的一種優(yōu)化模型，最早由J.Holland教授于1975年提出。遺傳算法中種群中的每個(gè)個(gè)體都是解空間上的一個(gè)可行解，通過模擬生物的進(jìn)化過程，進(jìn)行遺傳、變異、交叉、復(fù)制從而在解空間內(nèi)搜索最優(yōu)解。 ? 在KdV方程的挖掘（圖25）中，遺傳算法比稀疏回歸更為有效，這是因?yàn)閷?duì)于更大的備選集，DL-PDE中使用稀疏回歸時(shí)將需要更大的稀疏性，這會(huì)增加挖掘難度。DLGA-PDE可以在非完全備選集的情況下挖掘PDE，并且待挖掘的PDE項(xiàng)可以通過基因組的變異和交叉產(chǎn)生，可以避免出現(xiàn)DL-PDE中遇到的備選集大小問題。 ?

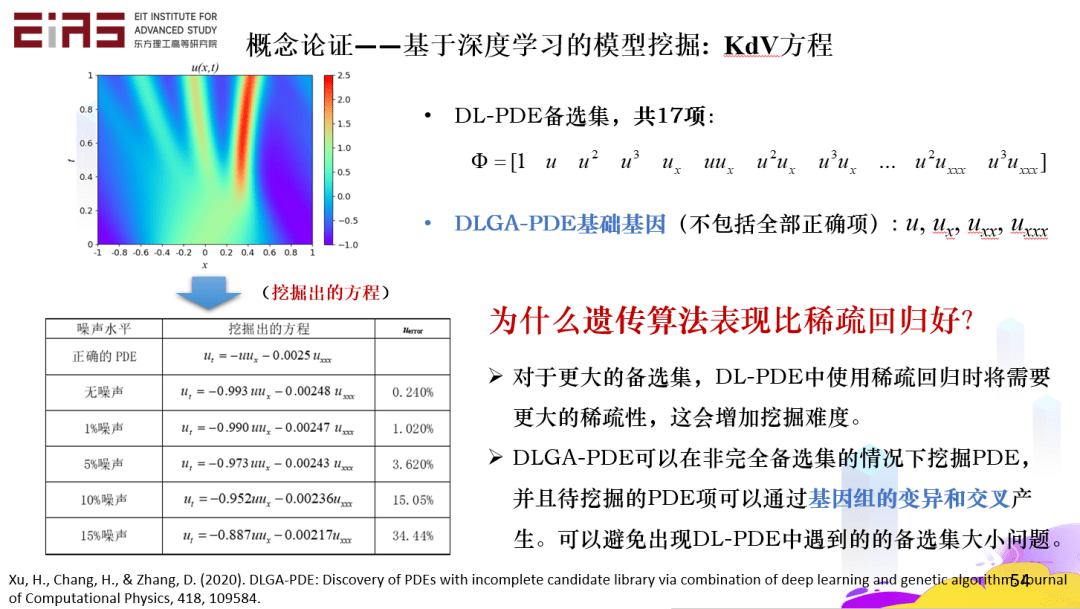
? 圖25 基于深度學(xué)習(xí)的模型挖掘——KdV方程 ? 3.3.3 開放候選集方法：符號(hào)數(shù)學(xué) ? 在一個(gè)自變量、一個(gè)因變量的情況下，定義一些運(yùn)算符、運(yùn)算法則，那么方程的每一項(xiàng)都是一個(gè)樹的結(jié)構(gòu)，再通過一次次變異去改變樹的結(jié)構(gòu)，就可以挖掘出控制方程（圖26），即使是比較復(fù)雜的方程也能被挖掘，這只需要自變量和因變量。

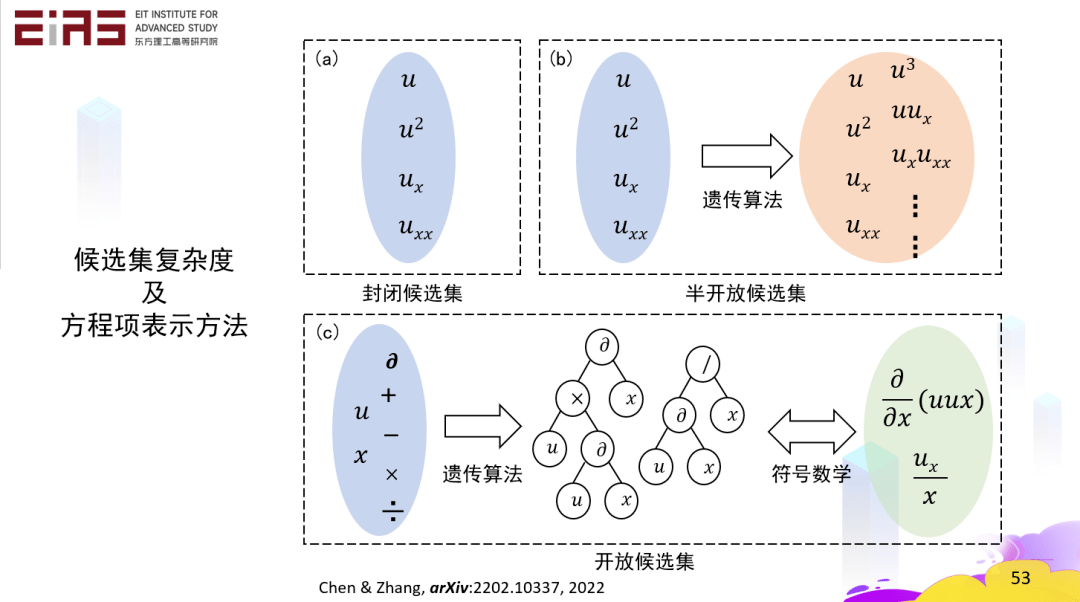
? 圖26 候選集復(fù)雜度及方程項(xiàng)表示方法 ? 3.4 基于知識(shí)發(fā)現(xiàn)和符號(hào)數(shù)學(xué)實(shí)現(xiàn)控制方程自挖掘（生產(chǎn)知識(shí)） ? 找到最適合數(shù)據(jù)的偏微分方程的關(guān)鍵在于解決兩個(gè)問題，一是如何通過符號(hào)數(shù)學(xué)表示任何給定的復(fù)雜開放式偏微分方程，二是如何使用機(jī)器學(xué)習(xí)算法從偏微分方程的無限可行域中挖掘正確的方程。 ? 引入符號(hào)回歸中樹結(jié)構(gòu)的概念，在開放空間中挖掘方程形式，每一項(xiàng)都可以變成一個(gè)樹的結(jié)構(gòu)，這個(gè)樹由節(jié)點(diǎn)構(gòu)成，父節(jié)點(diǎn)為運(yùn)算符（包括偏微分算符），子節(jié)點(diǎn)為系數(shù)、變量或函數(shù)，對(duì)樹結(jié)構(gòu)的深度和廣度都可以調(diào)整，表明樹或者說方程的項(xiàng)的復(fù)雜程度（圖27）。如此一來，任何方程都是一片森林，森林里的樹代表不同的方程項(xiàng)，通過遺傳算法、符號(hào)數(shù)學(xué)等方式能夠挖掘出自由形式的方程，即使方程的形式非常的復(fù)雜。（圖28） ?

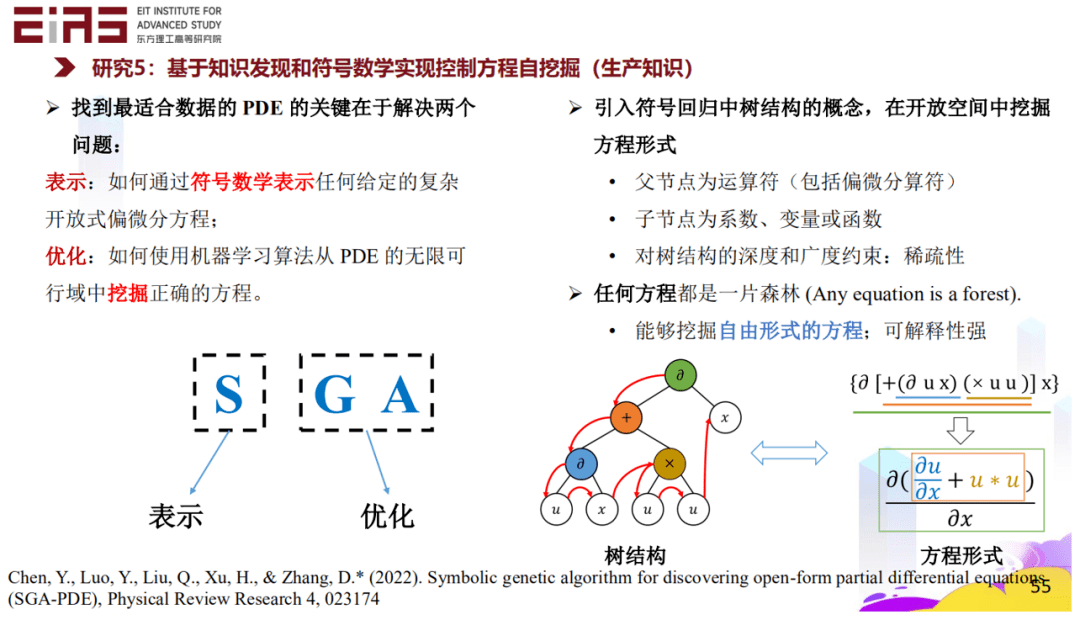
? 圖27 基于樹結(jié)構(gòu)挖掘自由形式的方程 ?

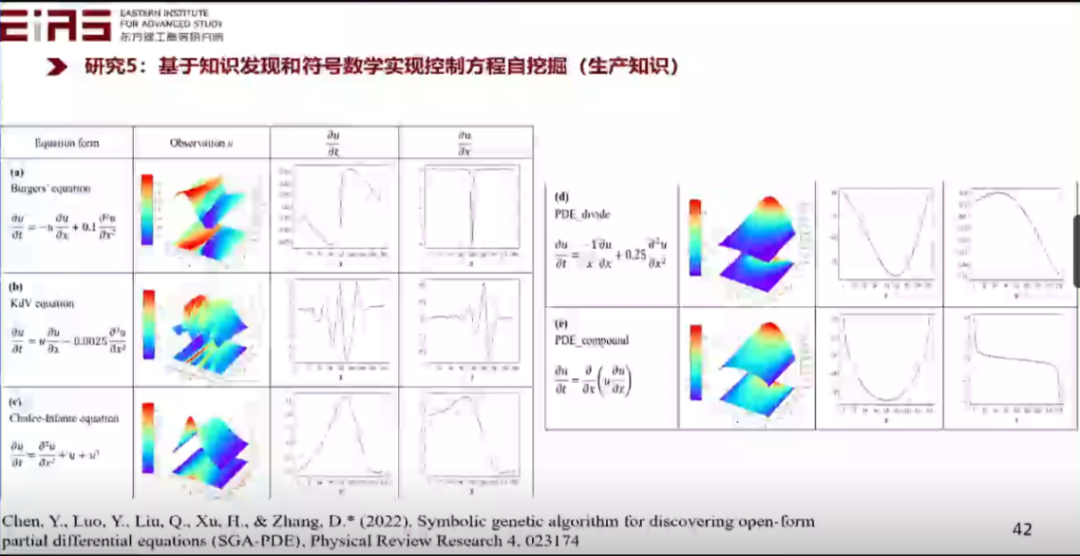
? 圖28 基于知識(shí)發(fā)現(xiàn)和符號(hào)數(shù)學(xué)實(shí)現(xiàn)控制方程自挖掘 ? 3.4.1 挖掘“分式結(jié)構(gòu)方程” ? ? 在分式結(jié)構(gòu)方程的挖掘過程中，初始有一個(gè)自變量、因變量，在第一代迭代后可能找出了這些簡單的項(xiàng)，但這些項(xiàng)是不正確的，再經(jīng)過幾十代的迭代，不斷地交叉、變異、進(jìn)化，最后挖掘出正確的方程（圖29、30），即使這是一個(gè)極其復(fù)雜的方程。 ?

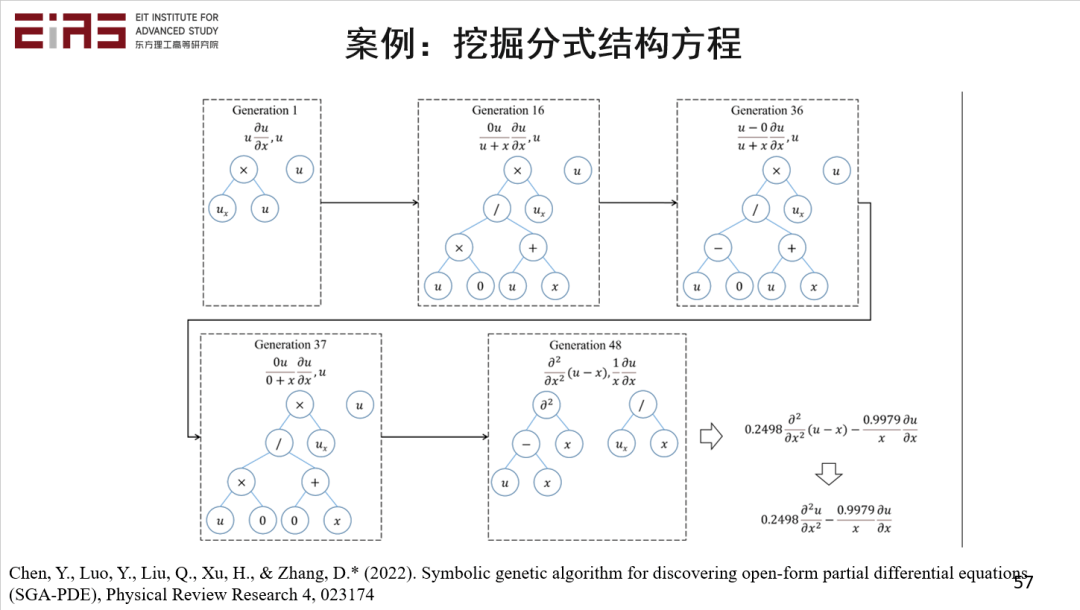
? 圖29 挖掘“分式結(jié)構(gòu)方程”（1） ? ?

? 圖30 挖掘分式結(jié)構(gòu)方程（2） ? 3.4.2 從細(xì)觀模擬數(shù)據(jù)中挖掘粘性重力流的宏觀控制方程 ? 知識(shí)發(fā)現(xiàn)也可以用來解決實(shí)際的問題，比如粘性重力流問題，通過控制方程的自挖掘，最終也能成功驗(yàn)證其數(shù)學(xué)上的合理性、物理上的預(yù)測(cè)性。粘性重力流的短期行為尚不存在控制方程，在這種情況下，通過精細(xì)的微觀數(shù)據(jù)模擬得到數(shù)據(jù)，并利用這些數(shù)據(jù)進(jìn)行學(xué)習(xí)，挖掘宏觀控制方程（圖31、32、33、34）。 ? 為了從數(shù)據(jù)空間中的原始仿真數(shù)據(jù)挖掘出語義空間中的可解釋的物理定律（PDE），需要以下三個(gè)步驟：數(shù)據(jù)重構(gòu)，基于深度神經(jīng)網(wǎng)絡(luò)（DNN）的替代模型訓(xùn)練；構(gòu)造語義片段，計(jì)算空間導(dǎo)數(shù)和積分通量；語義整合，基于遺傳算法挖掘出的簡約偏微分方程。 ?

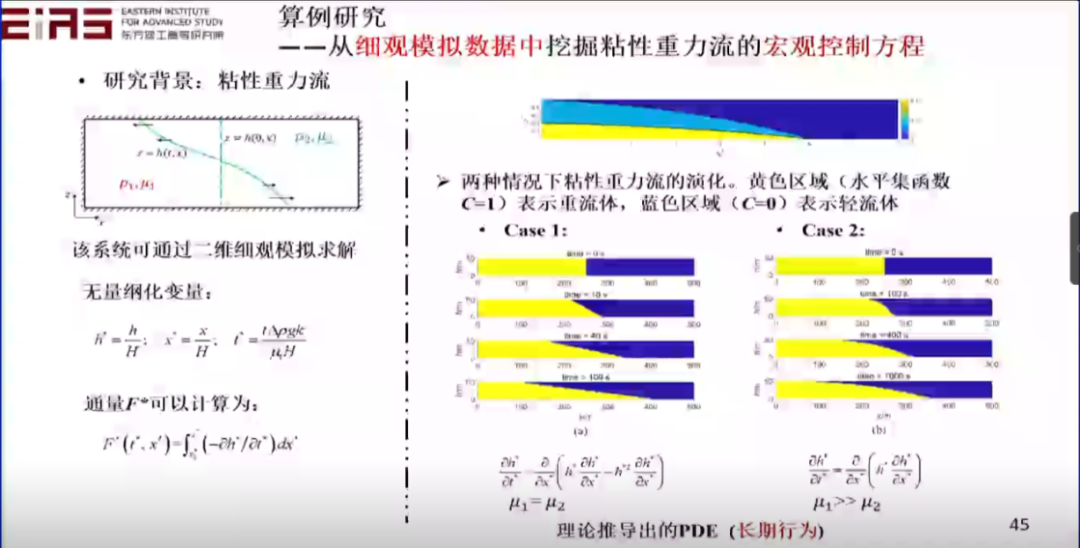
? 圖31 從細(xì)觀模擬數(shù)據(jù)中挖掘粘性重力流的宏觀控制方程 ?

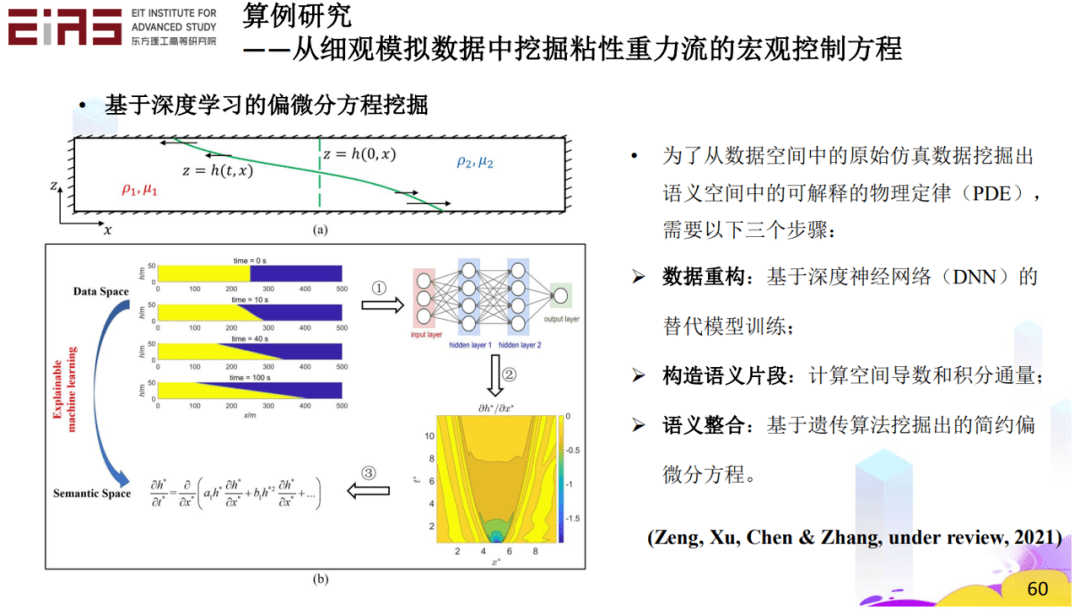
? 圖32 基于深度學(xué)習(xí)的偏微分方程挖掘 ?

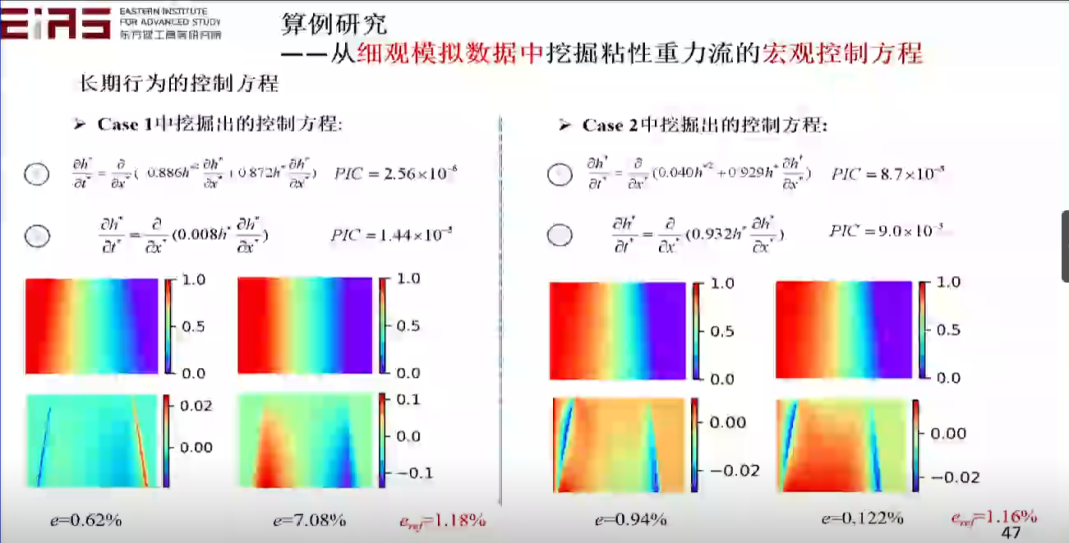
? 圖33 長期行為的控制方程 ?

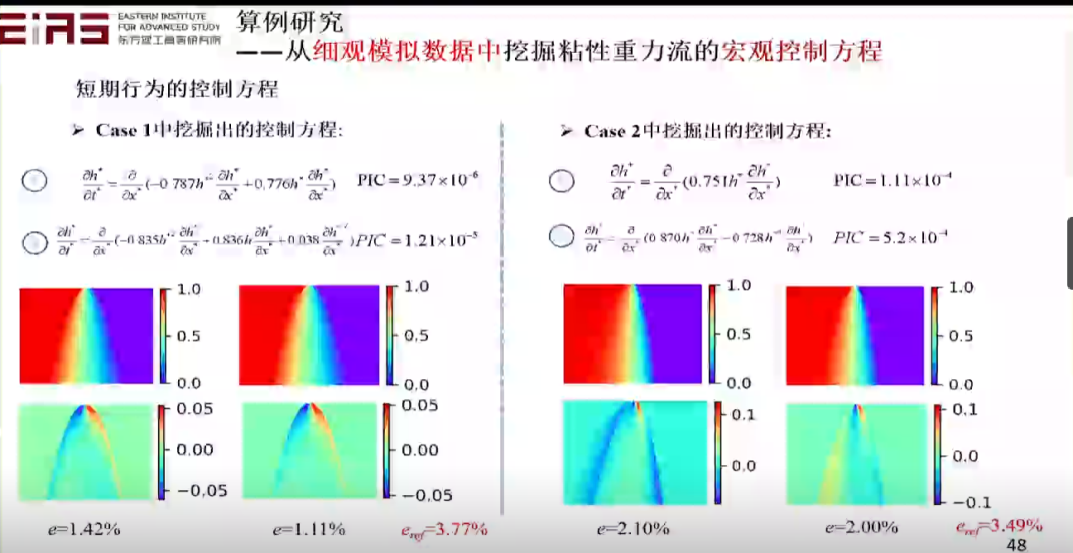
? 圖34 短期行為的控制方程

? ▍4、結(jié)束語

綜上所述，筆者認(rèn)為，機(jī)器學(xué)習(xí)算法可以有效地解決具有復(fù)雜非線性映射關(guān)系的問題。但數(shù)據(jù)是其基礎(chǔ)，在社會(huì)不斷向著信息化、數(shù)字化、智能化方向發(fā)展的過程中，從數(shù)據(jù)大要走向大數(shù)據(jù)，光有數(shù)據(jù)已然不夠，大數(shù)據(jù)技術(shù)將更具價(jià)值。其次，通過引入行業(yè)知識(shí)，可以有效提升機(jī)器學(xué)習(xí)模型的效果，可以在數(shù)據(jù)預(yù)處理、機(jī)器學(xué)習(xí)模型結(jié)構(gòu)以及模型效果評(píng)估環(huán)節(jié)嵌入領(lǐng)域知識(shí)，提升精度和魯棒性，同時(shí)還能在一定程度上降低數(shù)據(jù)需求。在“行業(yè)+AI”的未來，數(shù)據(jù)驅(qū)動(dòng)（機(jī)器學(xué)習(xí)）與模型驅(qū)動(dòng)（傳統(tǒng)模型）要得到有機(jī)結(jié)合（圖35），而核心就在于知識(shí)的嵌入和知識(shí)的發(fā)現(xiàn)，只有當(dāng)二者形成一個(gè)閉環(huán)，才能大大提高人工智能解決實(shí)際問題的能力。

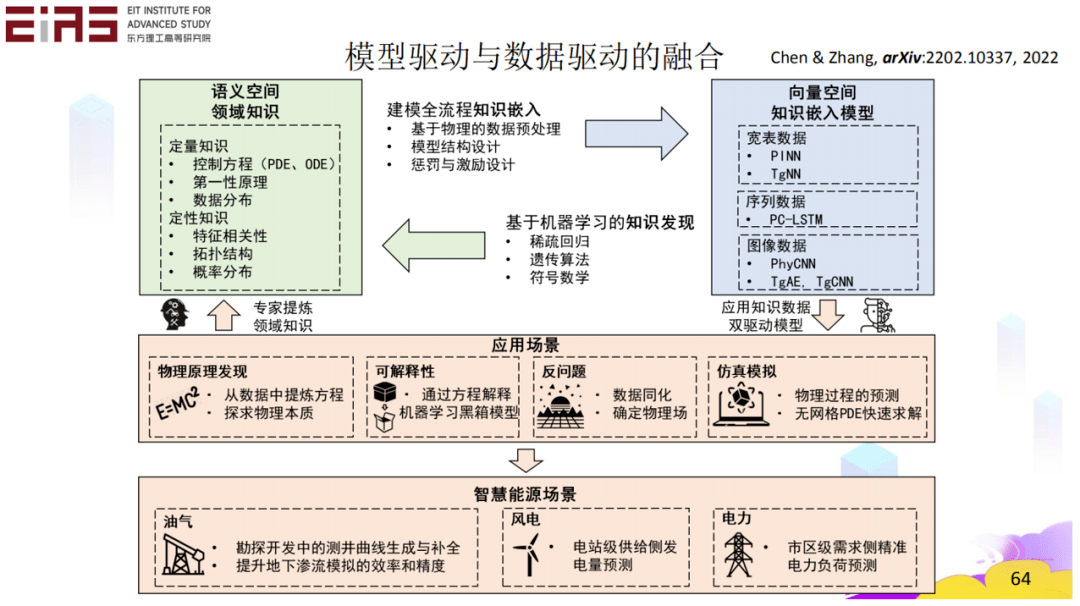
? 圖35 數(shù)據(jù)驅(qū)動(dòng)與模型驅(qū)動(dòng)的融合

? 編輯：黃飛

?