代碼倉庫地址：https://github.com/Oneflow-Inc/one-yolov5歡迎star one-yolov5項目 獲取最新的動態。?

摘要

邊界框回歸是目標檢測的關鍵步驟，在現有方法中，雖然-norm loss 被廣泛用于邊界框回歸，但它不是針對評估指標量身定制的，即 Intersection over Union (IoU)。最近，已經提出了 IoU 損失和generalized IoU (GIoU) Loss作為評估IoU的指標 ，但仍然存在收斂速度慢和回歸不準確的問題。在本文中，我們通過結合預測框和目標框之間的歸一化距離來提出距離-IoU (DIoU) Loss，它在訓練中的收斂速度比 IoU 和 GIoU Loss快得多。

此外，本文總結了邊界框回歸中的三個幾何因素，即

重疊面積（overlap area）、中心點距離（central pointdistance）和高寬比（aspect ratio），在此基礎上提出了完全 損失，從而促進了更快的收斂和更優的性能。通過將 結合到最先進的目標檢測算法中，例如 YOLO v3、SSD 和 Faster RCNN，我們不僅在 IoU 指標方面而且在 GIoU 指標方面都獲得了顯著的性能提升。此外，DIoU 可以很容易地用于非最大抑制（NMS）作為標準，進一步促進性能提升。注釋:這里IoU指標方面和GIoU指標方面指的是在：目標檢測精度測量(mAP值),IoU損失計算穩定性等一些方面。

目標檢測是計算機視覺任務中的關鍵問題之一，幾十年來一直受到了廣泛的研究關注 (Redmon et al. 2016;Redmon and Farhadi 2018; Ren et al. 2015; He et al. 2017;Yang et al. 2018; Wang et al. 2019; 2018).通常，現有的目標檢測方法可以分為：

單階段-檢測，如YOLO系列(Redmon et al. 2016; Red- mon and Farhadi 2017; 2018)和SSD (Liu et al. 2016; Fu et al. 2017),

兩階段檢測，如R-CNN系列檢測 (Girshick et al. 2014; Girshick 2015; Renet al. 2015; He et al. 2017),

甚至是多階段的檢測, 像CascadeR-CNN (Cai and Vasconcelos 2018). 盡管存在這些不同的檢測框架，但邊界框回歸預測一個矩形框來定位目標對象仍然是其中關鍵步驟。

前言

本文主要是結合論文Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression(https://arxiv.org/pdf/1911.08287.pdf) 對 IoU 的解析學習。

IoU

IoU介紹

Intersection over Union (IoU)

在指標評估概述的小節有介紹過IoU,已經對IoU有了初步的認識(其實在yolov5項目中并不是簡單的使用，而是用的后面介紹的CIoU )
計算公式：

(1)

是真實回歸框(gt:ground-truth),

是預測回歸框。

IoU loss

計算公式:

(2)

IoU Loss 優缺點分析

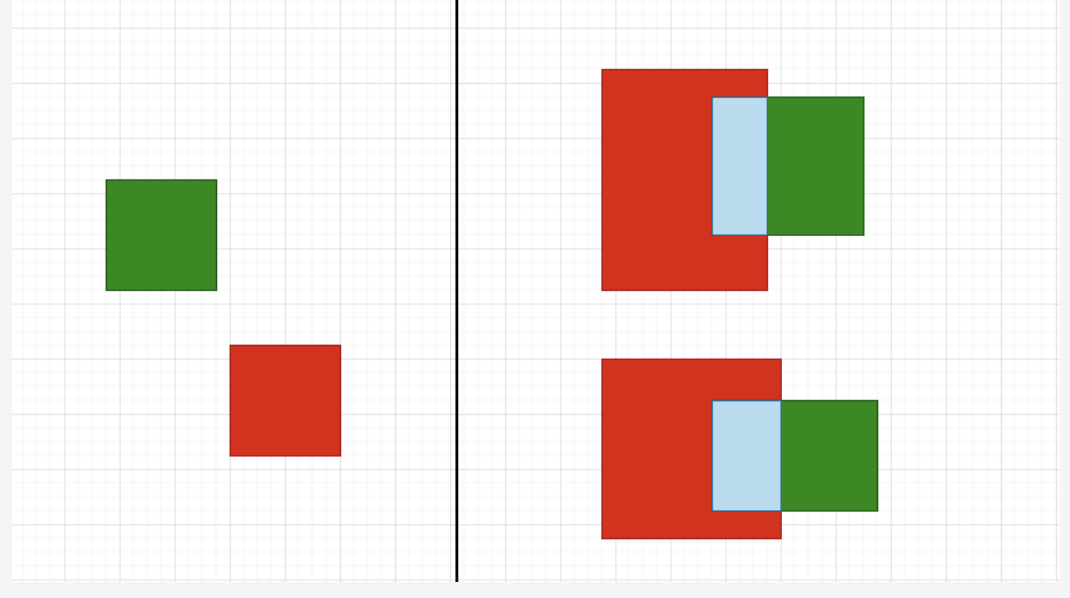
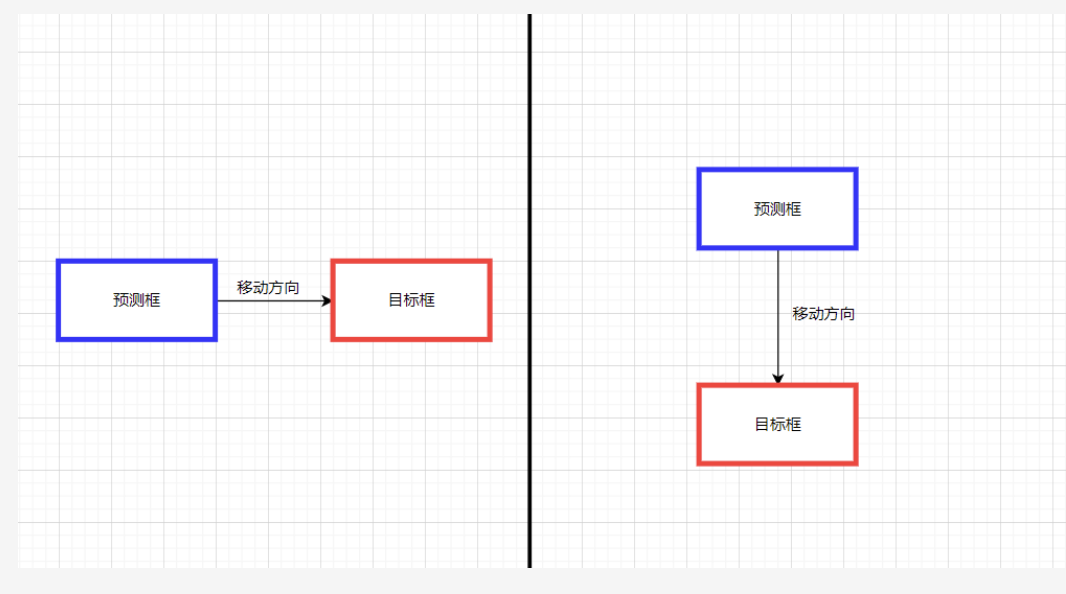
有明顯的缺陷 IoU loss只在邊界框有重疊時才能工作, 對于不重疊的情況不會提供任何移動梯度 (移動代表預測框朝著目標框重疊的方向移動) 。移動梯度表示無法衡量完全不相交的兩個框所產生的的損失（iou固定為0），和兩個不同形狀的預測框可能產生相同的loss（相同的iou）分別如下圖的左邊和右邊所示。

GIoU

GIoU介紹

GIoU的設計初衷就是想解決IoU Loss存在的問題（預測框與真實框不相交時iou恒定為0），設計了一套Generalized Intersection over Union Loss。在IoU的基礎上，GIoU還需要找到預測框和真實框的最小外接矩形，然后求出最小外接矩形減去兩個預測框union的面積，具體算法流程如下：

GIoU loss

計算公式 :

(3)

其中 ?是覆蓋 ?和 的最小方框,由于引入了，在不重疊的情況下，預測框也會向目標框移動。

GIoU 優缺點分析

GIoU Loss解決了IoU Loss在不相交情況的問題，在所有性能指標中都可以作為IoU的適當替代品，在目標檢測任務中能夠得到更高的準確率。

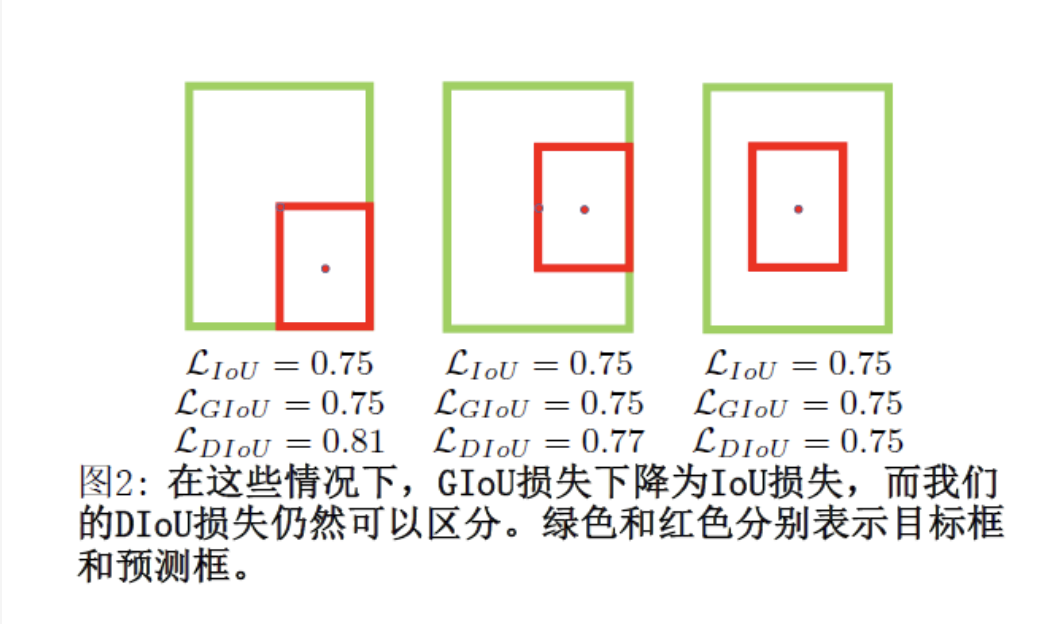
缺點：雖然GIoU可以緩解重疊情況下的梯度消失問題,但它仍有一些局限性。即無法衡量有包含關系時的框回歸損失，如下圖，三個回歸框具有相同的GIoU Loss，但是顯然第三個框的回歸效果更好。

IoU & GIoU 分析

首先，在本文上部分我們分析了關于原始的IoU損失和GIoU 損失的局限性。下面將通過模擬實驗結果對邊界框回歸的過程進行進一步的解析。(補充說明: 為什么要進行模型實驗? ?因為僅僅從檢測結果來分析邊界框回歸的過程很難，因為在不受控制的基準中的回歸情況往往不全面比如：不同的距離(distances),不同的尺度(scales)和不同的長寬比(aspect ratios)。相反，進行模擬實驗，在實驗中綜合考慮回歸情況，然后就可以很容易地分析給定損失函數的問題。)

模擬實驗

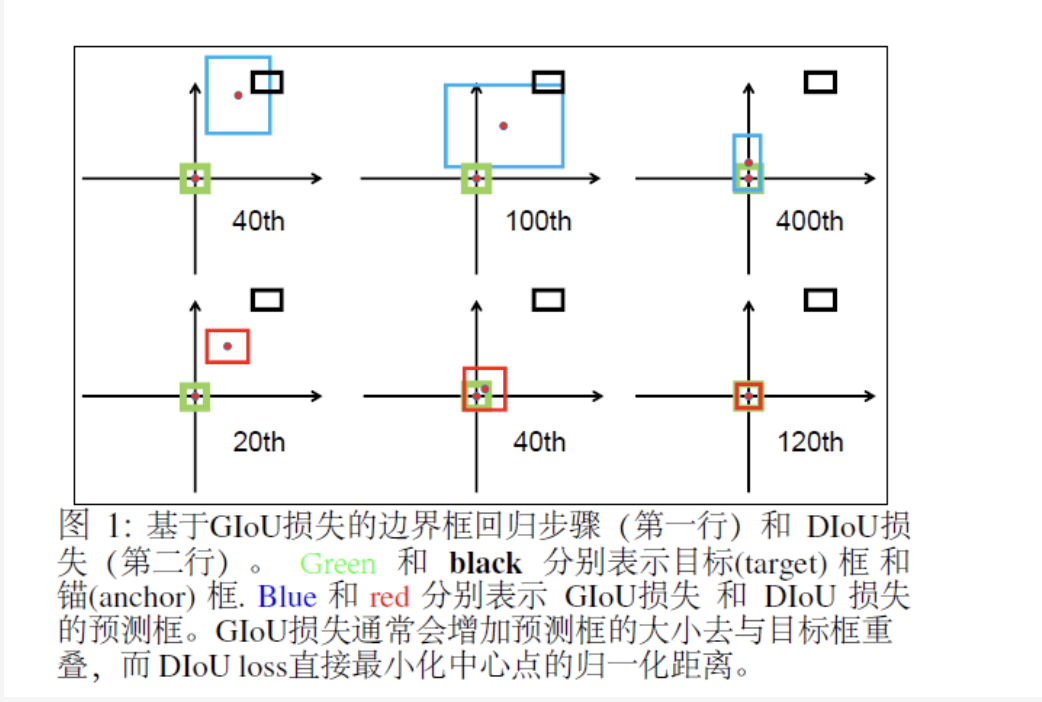
在模擬實驗中, 我們試圖通過距離(distances), 尺度 (scales)和長寬比(aspect ratios)來覆蓋邊界框之間的大部分關系，如圖3(a).所示。特別是, 我們選擇7個單位框 (即每個框的面積為 1) ，具有不同的長寬比 (即 ) ?作為目標框。在不失一般性的情況下，7個目標框的中心點被固定在。錨框均勻地分散在5000個點上。

距離: 在以半徑為 3 的 為中心的圓形區域內, 均勻選擇5000個點, 放置7個尺度、7個長寬比的錨 框。在這些情況下，重疊和不重疊的方框都被包括。

尺度:對于每個點, 錨框的面積分別設置為。

長寬比: 對于給定的點和尺度, 采用 7 個長寬比, 即與目標框遵循相同的設置 (即 ) 。所有 ?錨箱都對應在每個目標框。綜 上所述，總共有 ? ?個回歸案例。

圖3: 仿真實驗: (a) 通過考慮不同的距離、尺度和長寬比, 采用了171.5萬個回歸案例。(b)回歸誤差和（即: ? ?) 迭代次數為 ? ?時不同損失函數的曲線。

然后通過給定損失函數 , 我們可以用梯度下降算法 來模擬每種情況下的邊界框回歸過程。對于預測框 ? , 當前的預測可以通過:

(4)

其中 ? ?是迭代 ? ?時的預測框, ?表示損失的梯度。 感覺可以理解為學習率。值得注意的是，在我們的實現中，梯度乘以 ?去加速收斂。邊界框回歸的性能評估通過使用 ? 對于每個損失 函數, 仿真模擬實驗當達到迭代 ? ?時, 誤差曲線如 所示。

IoU 和 GIoU 損失的限制

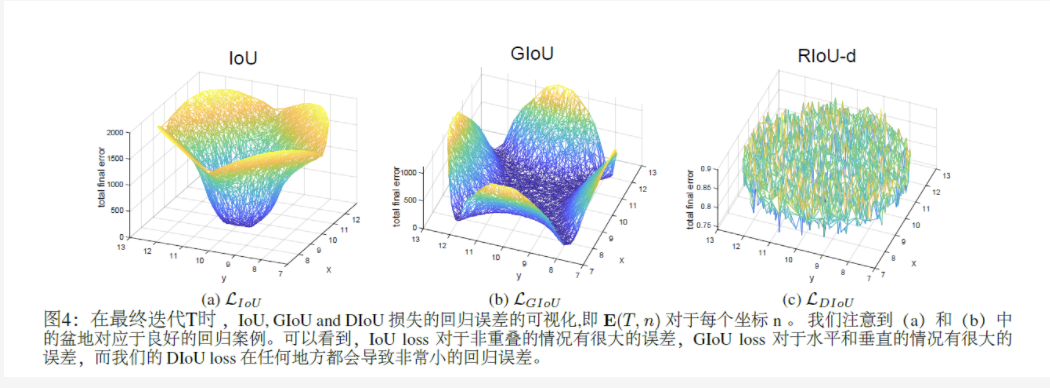
在圖4中，我們可視化迭代T時對5000個分散點的最終回歸誤差。

從圖4(a)中很容易看出，IoU損失只適用于與目標框重疊的情況。由于?B總是0，沒有重疊的錨框將不會移動。通過添加一個懲罰項見公式(3),

GIoU 損失能夠更好的緩解非重疊 案例的問題，如圖所示4(b), 但GIoU的損失顯著擴大了盆地，即GIoU的工作面積。但是，在水平方向和垂直方向的情況下，仍然很可能有很大的誤差。這是因為GIoU損失中的懲罰項是用來最小化|C?A∪B|，但是C?A∪B的面積通常很小或為0（當兩個盒子有包含關系時），然后GIoU幾乎退化為IoU損失。只要以適當的學習速率運行足夠的迭代GIoU 損失能收斂到很好的解決方案，但收斂速度卻是非常慢。從幾何上來說，從如圖1所示的回歸步驟來看，GIoU實際上增大了預測的框大小，用來和目標框重疊，然后IoU項用于預測框與目標框匹配，產生非常緩慢的收斂。

綜上所述，在非重疊情況下，IoU損失收斂是糟糕的解決方式，而GIoU損失收斂速度較慢，特別是對于水平和垂直方向的框。在目標檢測流程中，IoU和GIoU的損失都不能保證回歸的準確性。

DIoU & CIoU

通過前面的IoU和GIoU的分析我們很自然會問以下問題：

第一，是否可以直接最小化預測框和目標框之間的歸一化距離，以實現更快的收斂？

第二，當與目標框有重疊甚至包含時，如何使回歸更準確、更快？

DIoU loss

Distance-IoU 損失：更快更好的邊界框回歸損失,一般來說, 損失可以定義為

(5)

其中 ? ?是 預測框 ?B ?和目標框 ? ?的懲罰項。通過設計適當的懲罰項, 在本節中, 我們提出了 DIoU 損失和CIoU損失來解答上述兩個問題。

為了回答第一個問題, 我們提出將兩個邊界框的中心點之間的標準化距離最小化，懲罰項可以定義為

(6)

其中 ? ?和 ? ?分別代表 ?B ?和 ? ?的中心點。 ?為歐氏距離, ? ?是覆蓋兩個盒框的最小封閉框的對角線長度。損失函數可以定義為:

(7)

如圖5所示, 損失的懲罰項直接使兩個中心點之間的距離最小化, 而 ? ?損失的目的是減少 ? 的面積。

imgs

DIoU 和 IoU/GIoU 損失比較

新提出的DIoU損失繼承IoU和GIoU損失的一些屬性

DIoU損失對回歸問題的尺度仍然是不變的

與GIoU損失類似, DIoU損失可以在與目標框不重疊時為邊界框提供移動方向。

當兩個邊界框完美匹配時, 當兩個框都很遠時, ?

DIoU損失比IoU損失和GIoU損失有幾個優點, 可以通過仿真實驗進行評估。

如圖1和圖3所示, 可以直接最小化兩個框的距離, 因此收斂速度比要快得多。

對于兩個框是包含關系的情況(圖2), 或在水平和垂直方向的情況(圖6)下, 可以回歸非常快, 而 ?損失幾乎退化為 ?, 即

Complete IoU Loss

接著我們回答了第二個問題，提出了邊界框回歸的良好 損失應該要考慮三個重要的幾何因素, 即重疊面積、中心點距離和長寬比。通過統一坐標, 考慮了重疊區域, 而嚴重依賴于。我們提出的 旨在同時考慮邊界框的重疊面積和中心點距離。然而, 邊界框的長寬比的一致性也是一個重要的幾何因素。因此，基于 ，通過添加長寬比的一致性來 提出:

(8)

其中 ? ?是一個正的權衡參數, 衡量長寬比的一致性。

(9)

則損失函數可以定義為:

(10)

(11)

通過重疊面積因子給予更高的優先回歸, 特別是對于非重疊情況。最終, 的優化與 的優化相同, 除 了 ? ?的梯度應該指定 ? ?和。

(12)

主導器 通常是一個很小的值對于 ? ?和 ? ?的范 圍在 ?[0,1] , 這很可能會產生梯度爆炸。因此在我們的實現, 主導器 被移除, 將步長 ?替換為 , 梯度方向仍然與公式(12)一致。

NMS(Non-Maximum Suppression)

介紹

NMS是大多數目標檢測算法的最后一步，其中刪除了冗余的檢測框當它與最高分框的重疊超過一個閾值。Soft-NMS (Bodla et al. 2017) 用連續函數w.r.t.懲罰相鄰框的檢測分數IoU，產生比原始NMS產生更柔和大和更強大的抑制。IoU-Net (Jiang et al. 2018) 提出了一個新的網絡分支來預測定位置信度來指導NMS。最近，自適應NMS（Liu，Huang，和Wang 2019）和Softer-NMS（He et al. 2019）被提出分別研究適當的閾值策略和加權平均策略。在本工作中，簡單將DIoU作為原始NMS的標準, 在抑制冗余框時，同時考慮邊界框的重疊面積和兩個中心點之間的距離。

DioU-NMS

Non-Maximum Suppression using DIoU

在原始的NMS中, IoU指標用于抑制呂余的檢測框, 其 中重疊區域是唯一的因素, 對于有遮擋的情況，往往會 產生錯誤的抑制。我們在這項工作中建議 是 的更好標準，因為在抑制標準中不僅應考慮重疊 被正式定義為:

(13)

其中框 ? ?被去除通過同時到考慮 和兩個框中心點 的距離。? ?是分類得分和 ? ?是 閾值。我們認為兩 個中心點較遠的框可能會定位不同的物體, 而不應該被 刪除。此外 是非常靈活, 僅僅是幾行的代碼就可以集成到任何目標檢測管道中。

小結

在本文中，主要的介紹用于邊界框回歸的 和 和 用于抑制冗余檢測框的通過直接最小化兩個中心點的歸一化的距離，可以比實現更快的收斂。此外考慮了三個幾何屬性(即重疊區域、中心點距離 和 長寬比),促進了更快的收斂和更優的性能。

參考文章

https://github.com/Zzh-tju/DIoU/blob/master/README.md#introduction

https://github.com/Zzh-tju/DIoU/blob/master/README.md#introduction

IoU: https://arxiv.org/pdf/1608.01471.pdf

GIoU: https://giou.stanford.edu/GIoU.pdf

DIoU: https://arxiv.org/pdf/1911.08287.pdf

編輯：黃飛

?